習題變一變 思維現一現

趙方程

[摘 要]課堂教學中，教師應設計多樣化的習題，讓學生的思維活起來，真正經歷知識的發生、形成、發展過程，使學生在積極思考中獲得良好的學習效果。

[關鍵詞]習題 變化 思維 形成 發展 結構 知識

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）33-024

雖然長久以來練習一直飽受詬病，如練習重復、機械等問題長期突出，但從來沒有人提出數學學習應該取消練習。數學教學活動，特別是課堂教學應激發學生興趣，調動學生的學習積極性，引發學生的數學思考，培養學生的創造性思維。因此，教師要切實改變數學練習的現狀，從激發學生思維的角度出發，科學設計練習，提高數學練習的效率。

一、變一變，再現知識形成過程中的思維

毋庸置疑，看似簡單的數學知識，往往都經歷了漫長的發生、發展和形成過程。因此，課堂教學中，教師可變一變習題，再現知識的形成過程，這樣不僅利于激活學生的思維，而且有助于學生理解、掌握和運用知識。如學習測量后，書中大部分的練習如下：“黃瓜長20（ ），小陽立定跳遠跳了15（ ）。”如此類型的習題，考察的方面過于單一，教師可進行以下變化：“（1）同樣一根黃瓜，小明說有兩只手長，小亮說有一本書長，和你的同桌議一議，看看小明和小亮誰說得對。如果讓你說黃瓜的長度，你會怎么辦？（2）不測量，估一估你的數學課本寬度大約為（ ），估測后再實際測量數學課本寬度大約為（ ）。”這里，設計第（1）題旨讓學生在討論中再次經歷并思考統一單位必要性的認知過程，知道選用合適的測量工具進行測量；設計第（2）題旨在喚醒學生心中標準量的表象意識，使學生在思維變化中形成和鞏固對標準量的認識。

二、變一變，凸顯知識結構發展中的思維

數學知識既是相互發展的，又是相互聯系的。因此，課堂教學中，教師應讓學生了解數學知識之間的縱橫關系，使學生逐漸形成網絡化的知識結構，發展學生的整體思維和邏輯思維。如小學階段的加減法有整數加減法、小數加減法、分數加減法，雖然計算方法不太相同，但其中蘊含的算理都是一樣的，即相同計數單位才能相加減。所以，教學小數加減法時，教師可變化設計以下習題：計算并說一說豎式每一步算的是什么。（1）234+78，（2）3.4-0.9，（3）1.7+2.3。在學生算完后，教師追問：“為什么整數加減是末尾對齊，而小數加減是小數點對齊呢？”通過問題，讓學生思考知識之間的結構關系，形成完整的知識結構體系。

三、變一變，改變知識學習中的思維慣性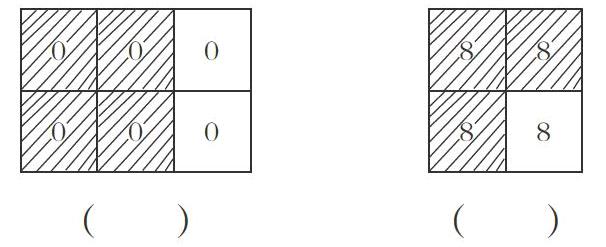

目前人教版小學數學教材一個學期一般設置七～十個單元，每個單元集中于一個知識內容的學習，這樣編排有助于學生短期內集中掌握一個知識內容，達到較理想的學習效果。但任何設計皆有利有弊，如學習乘法這一單元，學生面對問題時往往不假思索，直接列乘法算式解決，形成思維定式，出現了錯誤。因此，教師可變化設計以下練習：“（1）小明在超市里買了5瓶酸奶，每瓶4元，小明一共花了多少錢？（2）小紅在超市買了兩支鋼筆，一支8元，一支13元，小紅買鋼筆花了多少錢？”通過習題對比，讓學生自主打破思維定式，培養了學生認真審題的習慣，有效提高了學生分析問題、解決問題的能力。

四、變一變，引領知識生長的延伸思維

新知識都是從舊知識發展而來的，如果教師在教學中不能有效滲透知識間的內在聯系，將來學生在學習相關知識時，知識的直接生長點往往隱而不發，毫無作用，給教學帶來困難。如“分數的認識”在小學階段分四個層次進行教學：第一層次是將一個整體（單一的物體構成）平均分，用分數表示其中一份或幾份的大小；第二層次是將整體（可以有多個物體）平均分，用分數表示大小；第三層次是用分數表示除法；第四層次是用分數表示比。在人教版小學數學教材中，第一層次安排在三年級上冊教學，第二層次安排在五年級下冊教學，間隔時間長，如果不在三年級適當進行滲透、鋪墊，恐怕五年級又得從頭教起，費時費力。因此，在三年級教學后，教師可變化設計以下練習：“用適當的分數表示圖形中的陰影部分。”

這樣設計習題，雖然可以將整體看成單一的長方形或正方形，但整體中也蘊含了多個個體，溝通了第一層次和第二層次教學之間的聯系，為第二層次的教學提供了較為直接的知識支持和思維鋪墊。同時，教師還可以引導學生在填寫分數后具體說一說所填分數表示的實際意義，引發學生的思考，為學生的后續學習奠定基礎。

總之，習題變一變，看似簡單，實際上卻匠心獨具，既能培養學生的思維能力，又能讓學生有所習、有所思、有所得，實現減負的目的。

（責編 杜 華）