平面電路中的約束條件與電路方程的獨立性分析
◆李福新
平面電路中的約束條件與電路方程的獨立性分析
◆李福新
利用數學歸納法證明僅含有兩端元件的平面電路中支路、結點、網孔之間的關系,并由此得出平面電路中方程的獨立性原則,該原則是支路電流分析法的理論基礎。
平面電路;基爾霍夫定律;數學歸納法
10.3969/j.issn.1671-489X.2016.03.156
1 序言
在直流電阻電路的分析計算方法中,支路電流法是以支路電流為求解變量的電路分析方法[1]。支路電流法是根據各個元件上的VAR(元件約束)和電路各結點的KCL、網孔的KVL(拓撲約束)關系,以電路中各條支路上的電流為未知量,建立數目足夠且相互獨立的方程組,通過求網孔電壓KVL和結點的KCL結合列出足夠且相互獨立的方程組,并求解的過程。方法指出,可以根據電路中的結點數n,列出n-1個獨立的電流方程;根據電路中的網孔個數m,列出m個獨立的電壓方程。這樣,總的方程數(n-1)+m正好可以求解出電路中全部b條支路中的電路,即b=(n-1)+m。
考慮到拓撲約束證明的數學內容并非機電類工科學生的必修內容,且比較難掌握,在教學中通常只是讓學生記住此結論,而并不加以證明。有學生對此提出疑問:“電路的支路條數b、網孔數m和結點個數n肯定滿足以上關系嗎?如果有特例,豈不是無法正確求解?”
為了解答學生的疑問,筆者首先用數學方法證明以上結論的正確性,并在此基礎上討論平面電路方程的獨立性問題。
2 電路中的常用名詞
先明確電路中的幾個常用名詞的概念,這一點很重要。因為在不同的依據中,某些名詞概念的含義是不同的,特別是支路、結點的概念。本文中的支路是按照電路中同一電流習慣給出的,有別與網絡拓撲分析中的定義[2]。
1)平面電路:對于任意扭動電路的分支,將之鋪在一個平面上,若可以避免相交叉而又不連接的現象發生,則稱該電路為平面電路。換言之,平面電路就是可以畫在一個平面上而不使任何電路分支交叉的電路。本文中只討論僅含有兩端元件的平面電路,如圖1平面電路所示。
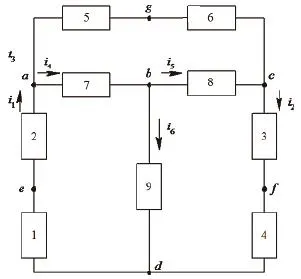
圖1 平面電路
2)支路(branch):電路中同一電流流過的分支電路全部。圖1電路中共有六個電流i1、i2、i3、i4、i5、i6,故此有六條支路。
3)結點(node):電路中三條或三條以上支路的公共連接點。圖1電路中有四個結點,分別是a、b、c和d,而e、f、g不是結點。
4)網孔(mesh):平面電路中的一個內部無任何支路的閉合回路。圖1電路中有三個網孔,分別是回路a→b→d→e→a、b→c→f→d→b、a→g→c→b→a。
5)基爾霍夫電流定律(KCL):靜態電路中,流經電路中任一結點的電流代數和恒等于0。
6)基爾霍夫電壓定律(KVL):任意時刻,沿電路任一回路繞行一周,回路中各個元件上的電壓的代數和恒等于0。
3 數學歸納法(Mathematical Induction)
數學歸納法是一種證明與自然數有關的命題的重要方法。一般的,證明一個與自然數n有關的命題P(n),有如下步驟:
1)證明當n取第一個值n0時命題成立,n0取0或1,或指定的某一具體數;
2)假設n=k(k≥n0,k為自然數)時命題成立,證明n=k+1時命題也成立;
3)綜合前兩步,對一切自然數n(n≥n0)都成立。
數學歸納法的三個步驟中,第一步是證明的奠基,第二步是遞推的依據,這兩個步驟都非常重要,缺一不可。
4 利用數學歸納法證明平面電路中的數學關系
根據以上所介紹的平面電路的基本概念及數學歸納法的證明步驟,若想證明b=(n-1)+m關系式對于任意平面電路都成立,不妨從m=1開始,電路如圖2所示。此電路中n=0,b=1,顯然滿足關系式b=(n-1)+m。

圖2 平面電路m=1
圖2電路是通過增加一條新支路的方法,得到兩個網孔的電路,即m=2。如圖3電路所示,此電路中支路條數b=3,結點個數n=2,很明顯也滿足b=(n-1)+m。
圖3 平面電路m=2
依然通過增加新支路的方法,得到三個網孔電路,即m=3,將會出現三種不同的電路,分別如圖4(a)(b)(c)所示。其中,圖4(a)中電路的結點數不變,即新增的支路是由原電路中的兩個結點之間接入,即n=2,此時支路數變為b=3+1=4;圖4(b)中電路的結點數n=3,即新增的支路是由原電路中的一個結點和增加一個新的結點(可以理解為原電路中的某一條支路上的一個點變為結點)之間接入,此時新電路的支路數b=3+1+2-1=5;圖4(c)中電路的結點數n=4,是由增加的連個新結點之間引入一條支路,則新電路支路數b=3+1+4-2=6。
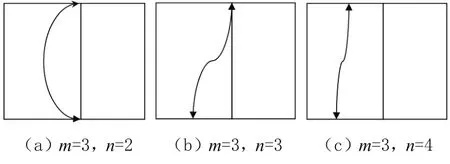
圖4 兩個網孔的平面電路
通過計算可以得出結論:三種情況中,均滿足關系式b=(n-1)+m。
現在假設某平面電路中的網孔數滿足m=μ(μ≥3,μ為自然數),結點數n=ν(ν為自然數)時,電路中支路條數b=(n-1)+m=(ν-1)+μ關系式成立,則通過增加一條新支路的方法使得網孔數增加1,即m=μ+1。如前所述分析可知,新電路會有三種情況出現:圖5(a)電路中n=ν,b=(ν-1)+ μ+1=(n-1)+m;圖5(b)電路中n=ν+1,b=(ν-1)+μ+1+2-1=(n-1)+m;圖5(c)電路中n=ν+2,b=(ν-1)+μ+1+4-2=(n-1)+m。
可見,對與網孔數為m=μ+1的平面電路,上述關系式依然成立。由以上分析,可知結論b=(n-1)+m對所有平面電阻電路均適用。
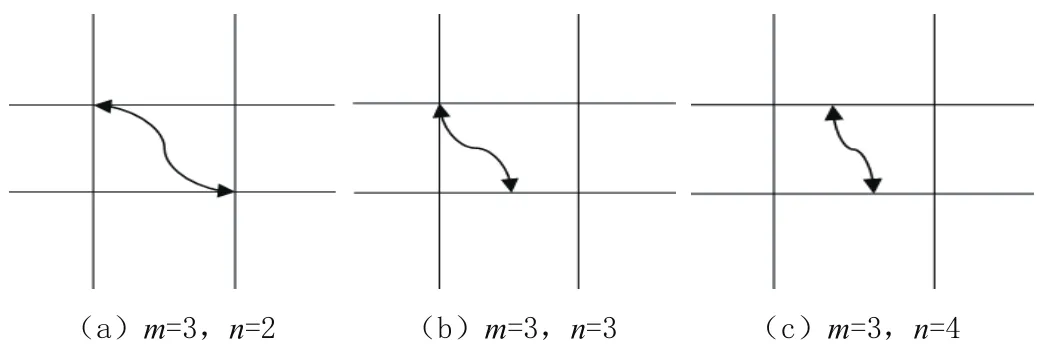
圖5 兩個網孔的平面電路
5 平面電阻電路中方程的獨立性
所謂的獨立方程,即任意一個方程都不能由所列的其他方程組合得到[4]。事實上,在一般情況下,對于有n個結點、b條支路的平面電路,可以列出n-1個獨立的KCL方程,這是因為對于n個結點中的前n-1個,可以分別列出獨立的KCL方程,而對于第n個結點,流入的電流其實可以表示為其他所有結點流出電流之和,流出的電流可以表示為其他所有結點流入電流之和,故此并非獨立方程;而在所列的各KVL方程中,可以確定的是以m個網孔為回路所列的KVL方程一定是相互獨立的,即b-(n-1)=m個,其他非網孔的回路所列的KVL方程可以由這m的獨立方程相加得到。因此,通過KCL和KVL所列的(n-1)+m個獨立方程,再加上VAR元件約束條件,可以求解出來任一平面電阻電路中全部b條支路上的電流。
[1]陸國和.電路與電工技術[M].3版.北京:高等教育出版社,2010.
[2]陳自力,劉學軍.克希霍夫獨立方程數定理的證明[J].電工教育,1995(3).
G 712
B
1671-489X(2016)03-0156-02
作者:李福新,天津中德職業技術學院基礎課部講師(300350)。

