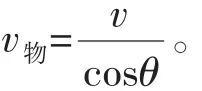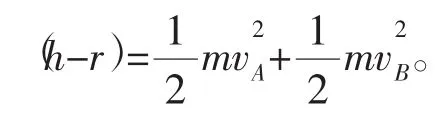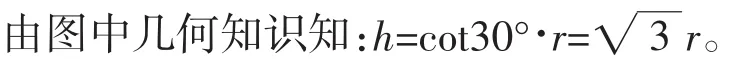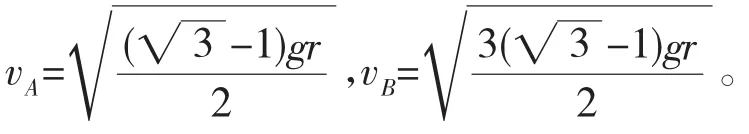把握運動合成與分解的本質
安徽省靈璧黃灣中學 華興恒
把握運動合成與分解的本質
安徽省靈璧黃灣中學 華興恒
運動的合成與分解問題對同學們來說難度較大,因為合成與分解方式的選擇不是隨心所欲的,而要根據(jù)實際情況來進行。下面我們一起來探究幾例,希望對同學們能夠有所啟迪。
一、正確判斷兩個直線運動合成后是曲線運動還是直線運動
物體做曲線運動的條件是物體所受合外力的方向與物體的運動方向不在一條直線上,即物體運動的速度方向與加速度方向不在一條直線上。顯然判斷合運動是曲線運動還是直線運動也應依據(jù)這一條件。具體判斷方法如下:(1)求出兩個直線運動的合初速度,即v=v1+v2;(2)求出兩個直線運動的合加速度,即a=a1+a2;(3)判斷合加速度a與合初速度v的方向關系。
若v=0但a≠0,則合運動為初速度為0的勻加速直線運動;若v≠0但a=0,則合運動為勻速直線運動;若v≠0且a≠0,且二者方向在同一條直線上,則合運動為勻加速直線運動;若v≠0且a≠0,且二者方向不在同一條直線上,則合運動為曲線運動。
例1關于運動的合成,下列說法中正確的是()。
A.兩個直線運動的合運動一定是直線運動
B.兩個不在同一條直線上的勻速直線運動的合運動一定是直線運動
C.兩個初速度為0的勻加速直線運動的合運動一定是勻加速直線運動
D.勻加速直線運動與勻速直線運動的合運動一定是直線運動
解析根據(jù)前面的分析可知,因選項A中兩直線運動的初速度與加速度都不明確,所以合成后的合初速度與合加速度的方向關系也不明確,故合成后運動是直線運動還是曲線運動也就無法確定,故選項A錯誤;因選項B中的兩個運動是勻速直線運動,合成后的合初速度是一個定值,合加速度為0,所以合成后的運動一定是勻速直線運動,故選項B正確;因選項C中兩個運動都是初速度為0的勻加速直線運動,合加速度是一定值,合初速度為0,合成后的運動一定是初速度為0的勻加速直線運動,故選項C正確;雖然選項D中兩個運動合成后的加速度很明確,可是由于勻加速直線運動的初速度不明確,所以導致兩個運動合成后的初速度方向不明確,則合成后的合初速度與合加速度的方向關系不明確,則合成后運動是直線運動還是曲線運動也就無法確定,故選項D錯誤。本題應選B、C。
二、對拉船上岸模型問題要能正確地分解
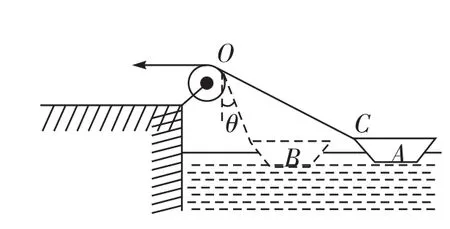
圖1
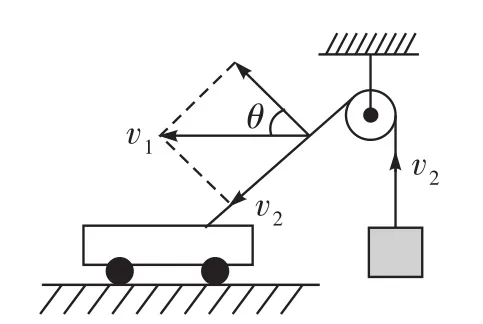
圖2
如圖1所示,用輕繩將小船由位置A拉到位置B,會有下面的兩種效果產生:(1)定滑輪O到船頭C這段繩子的長度變短;(2)輕繩與豎直方向的夾角θ變小。
若假設輕繩與豎直方向的夾角保持不變,只有繩OC縮短,這樣小船就會沿繩運動;若假設輕繩OC段的長度保持不變,輕繩與豎直方向的夾角減小,這樣小船就會以O為圓心、以繩OC的長度為半徑做圓周運動,在C點的線速度沿切線方向,垂直于半徑OC。顯然小船同時參與兩個運動:一個是沿半徑方向(即繩CO方向)的直線運動,另一個是以OC為半徑的圓周運動。
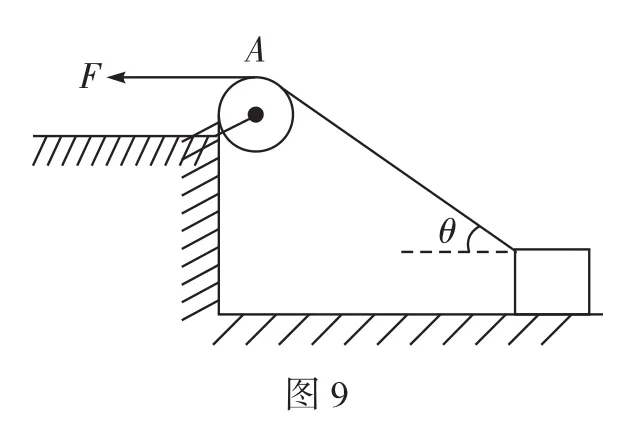
例2如圖2所示,在水平地面上做勻速直線運動的汽車,通過定滑輪用繩子吊起一個物體,若汽車與被吊物體在同一時刻的速度分別為v1和v2,則下列說法正確的是()。
A.物體在做勻速運動,v2=v1
B.物體在做加速運動,v2>v1
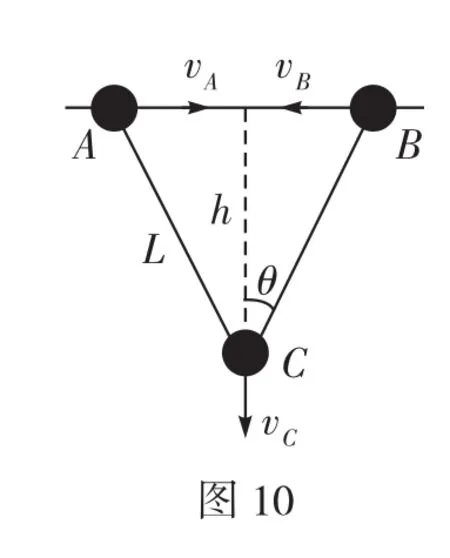
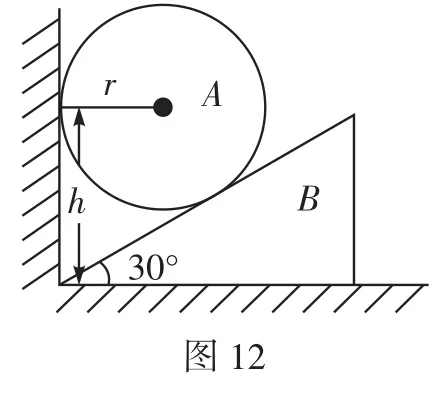
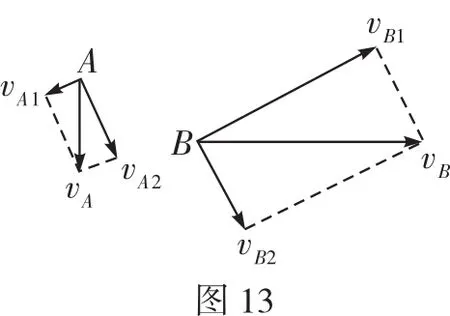
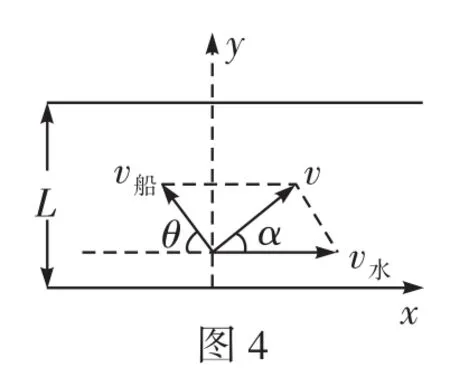
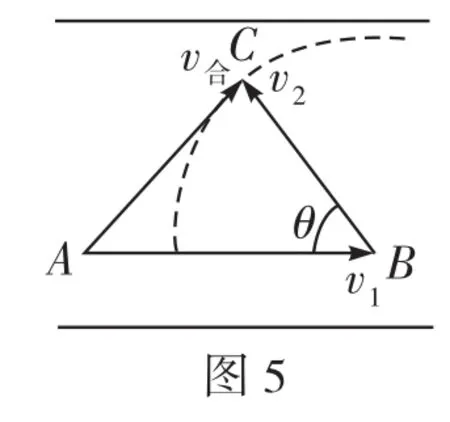
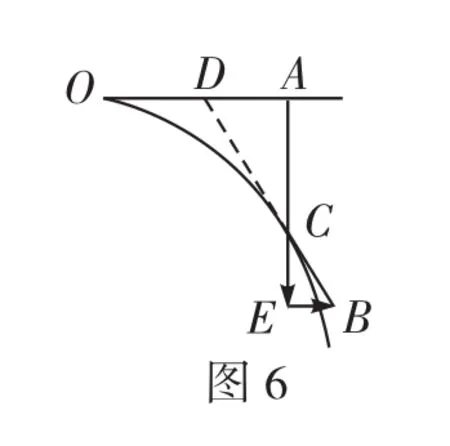
C.物體在做加速運動,v2 D.物體在做減速運動,v2 解析因汽車的運動導致兩個效果:一個是滑輪到汽車之間的繩子變長,另一個是滑輪到汽車的繩子與豎直方向之間的夾角變大。顯然汽車的運動由沿繩的方向的直線運動和垂直于繩的方向的圓周運動合成,所以汽車的運動應從沿繩和垂直于繩的兩個方向進行分解,如圖2所示。 根據(jù)圖中所示的分解,有v2=v1sinθ,由于v1是恒量,θ逐漸增大,所以v2增大,即物體加速上升,且v2 如果水流的速度大于小船在靜水中的航行速度,則不論小船怎樣航行,都會被水沖向下游,那么怎樣才能使得小船漂向下游的距離最小呢?如圖4所示,設船頭(v船)與河岸成θ角,合速度(v)與河岸成α角,容易看出α角越大,船漂向下游的距離越短。在什么條件下α角最大呢?可以以v水的矢尖為圓心,以v船的大小為半徑畫圓,當v與圓相切時,α角最大。 例3如圖5所示,河水流速v1=5 m/s,一只小機動船在靜水中的航行速度v2=4 m/s。現(xiàn)在它從A點開始渡河,要使其位移最短,船頭應指向何方航行? 例4如圖7所示,與水平面的夾角為θ的直角三角形木塊(斜面足夠長)固定在地面上,將一個可以看作質點的小球以初速度v0從三角形的頂點上水平拋出,試求小球距斜面的最遠距離是多大? 解析假設小球運動到B點時距離斜面最遠(如圖8),根據(jù)題意可知,此時小球的速度與斜面平行。作速度的反向延長線,與水平位移AF交于中點D,過B點作垂直于斜面的垂線BE,過D點作垂直于斜面的垂線DC,則BE=DC,BE即為小球到斜面的最遠距離。 如圖9所示,在一光滑水平面上放一物體,人通過細繩跨過高處的定滑輪拉物體,使物體在水平面上運動,人以大小不變的速度v運動。當繩子與水平方向成θ角時,物體前進的瞬時速度v物是多大? 此問題還可以利用微元法、運動的分解等方法求解,同學們不妨試一試。 例5在水平光滑細桿上串著A、B兩個剛性小球,兩球間距離為L,用兩根長度同為L的不可伸長的輕繩與C球連接,如圖10所示。開始時三球靜止,兩繩伸直,然后同時釋放三球。已知A、B、C三球質量相等,試求A、B兩球的速度vA或vB的大小與C球到細桿的距離h之間的關系。 解析求解本題的關鍵是要找到A、B兩球的速度和C球的速度之間的關系。易知vA=vB,在圖10所示的位置,BC繩與豎直方向成θ角。因為BC繩不能伸長且始終繃緊,所以A、B、C三球運動時的約束條件是B、C兩球的速度vB和vC(或A、C兩球的速度vA和vC)在繩的方向上的投影應相等,即vCcosθ= vBsinθ。 例6如圖11所示,均勻直桿連著兩個小球A、B,不計一切摩擦。當桿滑到如圖所示的位置時,B球水平速度為vB,加速度為aB,桿與豎直方向的夾角為θ,求此時A球速度vA和加速度aA的大小。 解析將B球速度和加速度沿桿的方向進行投影,則有vB′= vBcos(90°-θ),aB′=aBcos(90°-θ)。 設A球的實際速度為vA,其方向沿豎直方向,將它沿桿的方向進行投影,則有vA′=vAcosθ,aA′=aAcosθ。 因為A、B兩個小球連同桿一起運動時,桿始終伸直不彎曲,所以問題的約束條件是A球和B球的速度、加速度沿桿的方向進行投影時大小必定相等,即vBcos(90°-θ)=vAcosθ,aBcos(90°-θ)= aAcosθ。解得:vA=vBtanθ,aA=aBtanθ。 例7如圖12所示,斜劈B的傾角為30°,劈尖頂著豎直墻壁靜止于水平地面上,現(xiàn)將一個與斜劈質量相同、半徑為r的球A放在墻面與斜劈之間,并從圖示位置由靜止釋放,不計一切摩擦,求此后運動中:(1)斜劈的最大速度;(2)球觸地后彈起的最大高度(球與地面作用過程中機械能的損失忽略不計)。 A、B的運動均可沿斜面方向和垂直于斜面方向分解,如圖13所示。三、小船渡河問題

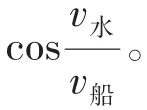
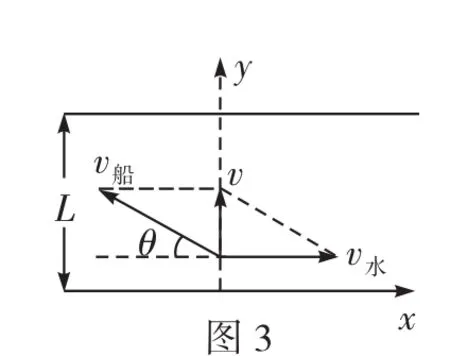
四、平拋運動問題
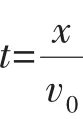
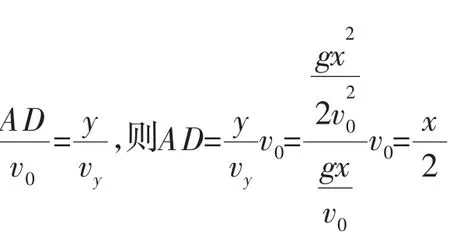
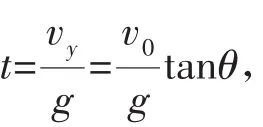
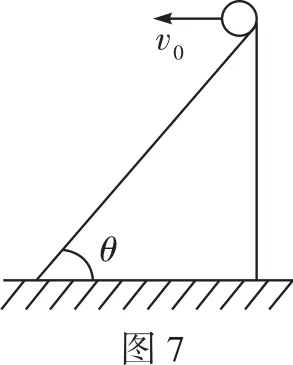
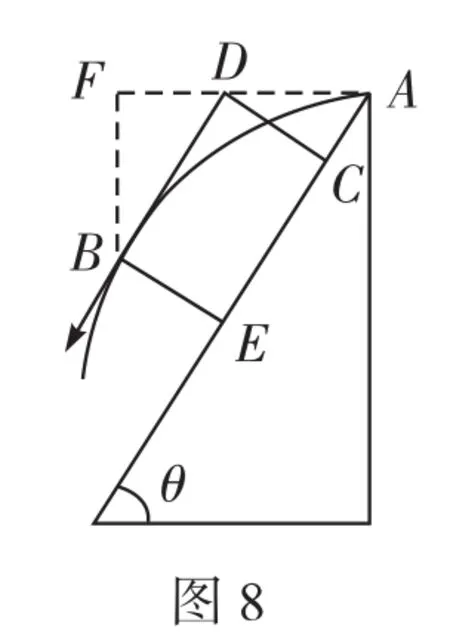
五、速度與加速度的關聯(lián)問題