懲罰廣義線性模型在遺傳關聯研究中的應用及R軟件實現*

廣東藥學院公共衛生學院流行病與衛生統計學系(510310)

張俊國　劉　麗　李麗霞　張　敏　郜艷暉△

?

懲罰廣義線性模型在遺傳關聯研究中的應用及R軟件實現*

廣東藥學院公共衛生學院流行病與衛生統計學系(510310)

張俊國劉麗李麗霞張敏郜艷暉△

【提要】目的遺傳關聯研究中高維數據與日俱增。本文探討基于嶺估計、LASSO和彈性網的廣義線性模型在遺傳關聯研究的應用及軟件實現，為高維關聯分析提供方法學參考。方法介紹懲罰廣義線性模型原理及軟件實現方法，并采用模擬的連鎖平衡和連鎖不平衡的SNPs關聯研究數據，以懲罰logistic模型例證R軟件glmnet包對廣義線性模型的擬合。結果對連鎖平衡和連鎖不平衡SNPs模擬數據，LASSO與彈性網均給出稀疏解，較好地選擇有關聯SNPs而剔除無關聯變量；而嶺估計把所有變量都保留在模型中，模型復雜度高但相應的解釋度未增加。結論LASSO和彈性網可對高維遺傳關聯數據進行有效降維，篩選變量的同時提供參數估計，從而降低模型的復雜度。R軟件的glmnet包靈活擬合各類懲罰廣義線性模型，可在高通量遺傳關聯分析中推廣應用。

懲罰廣義線性模型遺傳關聯研究LASSO彈性網glmnet包

近年來隨著高通量測序技術在遺傳流行病學研究中的應用，大量的高維遺傳關聯數據不斷涌現，如動輒成百上千甚至數以萬計的SNPs(single nucleotide polymorphisms)數據呈現高維度的特征，給遺傳關聯統計分析帶來極大挑戰[1]。在許多情況下，研究中響應變量的分布非正態，且與高維自變量的關系也非線性，因此統計分析可在廣義線性模型(generalized linear model，GLM)框架下實現[2]。廣義線性模型是經典線性模型的自然推廣，包含有一些極具實用價值的模型，如被學者廣為熟知的logistic回歸、計數資料中發揮重要作用的Poisson回歸等。在高維數據中運用廣義線性模型，其首要任務是降維，去除數據中的冗余信息或綜合數據中相關信息以減少自變量的個數[3]；而如何從這些高維數據中攫取有價值的信息，即變量選擇顯得尤為重要。

傳統廣義線性模型通過對數似然函數進行參數估計，系數估計值一般非零，自變量多時模型復雜度大大提高，而存在多重共線性時參數估計更易于失效。從模型簡潔度和解釋力的角度看，研究者希望從大量的預測變量中挑選盡量小的子集，用盡可能簡單的模型獲得最好的解釋效果[4]。針對傳統參數估計的缺陷，1970年Hoerl和Kennard提出嶺估計，在似然函數基礎上對系數平方進行懲罰(稱L2懲罰)，可在一定程度上解決共線性問題來提高模型的精確度[5]；但是它將系數壓縮趨于0卻不為0，因此不能給出簡單且解釋性強的模型。1996年Tibshirani提出稱之為LASSO(least absolute shrinkage and selection operator)的變量選擇方法，用模型系數的絕對值函數作為懲罰來壓縮模型(稱L1懲罰)，使絕對值較小的系數自動壓縮為0，同時實現變量選擇和參數估計[6]。然而在變量數p遠遠大于觀測值n的情形下，LASSO最多只能選擇n個變量，導致模型過于稀疏。因此Zou等學者在2005年提出將嶺估計和LASSO凸結合的懲罰方法，稱為“彈性網(elastic net)”，可有效解決該問題[7]。目前懲罰廣義線性模型可在R軟件中實現，運用Glmnet包可有效、靈活地擬合各類懲罰模型，為高維數據提供了有力的分析工具。本文采用模擬的SNPs關聯研究數據，以懲罰logistic模型例證glmnet包對廣義線性模型的擬合。

模型原理和方法

假定觀測值xi∈Rp，因變量yi∈R,i=1,…,N，并假定因變量取值為1和0，構建logistic模型為：

(1)

式(1)通常采用最大似然估計。而懲罰logistic回歸是在對數似然函數的基礎上，加入懲罰項[8]，通過最小化懲罰目標函數得到參數估計值，即：

(2)

研究表明，如果自變量間存在相關，嶺估計傾向于同時壓縮相關自變量的系數，而LASSO傾向于僅選擇相關自變量中的一個，彈性網則是嶺估計和LASSO的有效結合。設置α=0.5將傾向于將相關變量同時納入或同時排除，當α=1-ε(ε為雖小卻大于0的數值)時，會讓彈性網模型執行起來更傾向于LASSO，可以排除許多存在高度相關的變量。

懲罰logistic回歸的算法多采用坐標下降法(coordinate descent)，這是目前關于LASSO的最快計算方法[9]。算法原理為對每一個參數在保持其他參數固定的情況下進行優化循環，直到系數穩定為止。計算在λ的格點值上進行，而λ的確定可以通過k折交叉驗證(k-fold cross-validation)得出。

R軟件glmnet包的基本語法

R軟件中可使用glmnet包實現懲罰廣義線性模型[8]。glmnet能夠處理各種數據類型，擬合線性、多項式、logistic和Poisson回歸等廣義線性模型。它的正則化路徑是在λ的格點值上計算LASSO或者彈性網的懲罰項。主要函數為：

glmnet(x,y,family=c(“gaussian”,“binomial”,“Poisson”,“multinomial”,“mgaussian”),alpha=1,…)

上述語句可擬合廣義線性模型，得到正則化的路徑；其中，x為自變量矩陣，y為因變量，family中指定因變量的分布類型，默認各類分布的典型鏈接函數，如上述選擇項分別對應正態分布(恒等鏈接)，二項分布(logit鏈接)，Poisson分布(log鏈接)，多項分布(累積logit鏈接)和多元正態分布(恒等鏈接)；alpha是彈性網的混合參數，取值范圍為[0,1]。當設置alpha=1時擬合LASSO(缺省值)，alpha=0時擬合嶺估計；在(0,1)區間內擬合彈性網。實際應用中，alpha取值的選擇也可借助cv.glmnet函數，通過設定不同的alpha值進行交叉驗證：

cv.glmnet(x,y,nfolds,alpha,…)

上述函數可完成模型的K折交叉驗證，除選擇alpha值外，還主要用于確定模型的調整參數λ。其中x和y意義同前，nfolds指定交叉驗證的K值，表示將所有觀測隨機分為K份，循環采用K-1份作為訓練樣本，剩余1份作為驗證樣本，默認值為10，最小可設定為3。

模型擬合后，可用coef和predict函數顯示懲罰模型的參數估計值及據此模型進行預測：

coef(object,s=c(“lambda.1se”,“lambda.min”)or null,…)

predict(object,newx,s=c(“lambda.1se”,“lambda.min”)or null,…)

上述函數中，如對參數s進行設定，object定義為cv.glmnet交叉驗證選擇的模型，否則為glmnet估計的所有模型；s中lambda.min為交叉驗證結果中平均誤差最小的模型對應的值，lambda.1se則為最小平均誤差1倍標準誤內對應λ中的最大值；一般而言，定義Lambda.min輸出最優模型(平均誤差最小)，但可能存在模型復雜及過擬合的問題；定義Lambda.1se可輸出更簡潔的模型，但較最優模型存在相對誤差。此外，predict函數中的newx為參與預測的自變量矩陣。

實例分析

為說明懲罰廣義線性模型及R軟件glmnet包在遺傳關聯研究中的應用，本文采用病例對照設計的遺傳關聯研究模擬數據，探討不同的遺傳情景下各類懲罰模型的參數估計效果。數據模擬過程中，設置了連鎖不平衡(linkage disequilibrium，LD)參數，以反映群體中不同基因座上等位基因間的關聯。在模擬數據中LD定義為高維SNPs間的相關系數，分兩種情況：(1)SNPs變異間獨立(LD=0)；(2)SNPs間高度相關(LD=0.9)。病例組和對照組樣本量各為500，為便于說明glmnet包的輸出結果，模擬數據集中只包含20個SNPs，并隨機抽取其中5個(X1，X4，X5，X12，X15)設置為與因變量有關聯的SNPs，剩余15個設置為與因變量無關聯的噪聲變異；與疾病有關聯的變異效應值ORs均設為2。模擬數據在R軟件中完成，具體模擬方法參見文獻[10]。數據集形式為1000個觀測行，22個變量列，如表1所示。

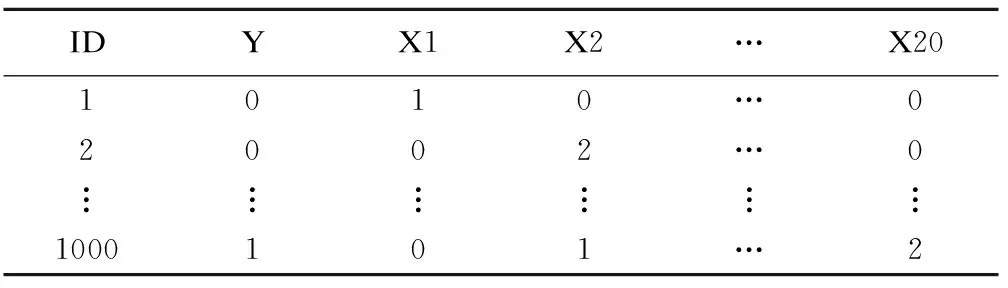
表1　數據集形式

實例分析時，先在R軟件中載入glmnet包，讀取R軟件工作目錄的數據，建立自變量和因變量矩陣；設定隨機數種子，可以保證結果的唯一性。例如對連鎖平衡數據集SAMPLE_LD0.csv擬合懲罰logistic回歸模型，具體程序為：

library(glmnet)#載入glmnet包

linkage<-read.csv(“SAMPLE_LD0.csv”)#讀入數據

linkage.x<-as.matrix(linkage[,3:22])#生成自變量矩陣

linkage.y<-as.matrix(linkage[,2])#生成因變量矩陣

set.seed(2015)#設定隨機數種子

link_glm<-glmnet(linkage.x,linkage.y,family=“binomial”)#擬合LASSO模型

plot(link_glm)#繪制系數正則化的路徑圖

由于因變量為二分類，故在glmnet函數的family選項中選擇binomial，alpha缺省時為1，擬合基于LASSO的懲罰logistic回歸；如定義為0或(0，1)之間的數值，則擬合基于嶺估計和彈性網的懲罰logistic回歸。Link_glm中包含不同取值時的所有模型。圖1為alpha=1，0和0.5時分別擬合LASSO，嶺估計和彈性網系數懲罰的收縮情況；其中橫坐標為L1正則化，即系數的絕對值之和，又稱曼哈頓距離；縱坐標為系數，上方數字是模型中保留的變量個數，圖中可看到系數在正則化路徑上的選擇。此例中LASSO和彈性網壓縮過程相似，可將部分系數連續壓縮為0，從而實現變量選擇的目的，而嶺估計壓縮系數的過程中仍保留所有變量在模型中。

為選擇適宜的λ值，使用cv.glmnet函數，通過交叉驗證觀察不同λ取值時的模型誤差，具體程序為：

link_cv <-cv.glmnet(linkage.x,linkage.y,nfolds=10,family=“binomial”)#10折交叉驗證

plot(link_cv)#繪制交叉驗證曲線圖

link_cv$lambda.min#最小誤差模型的lambda

link_cv$lambda.1se#1倍SE內的最大lambda

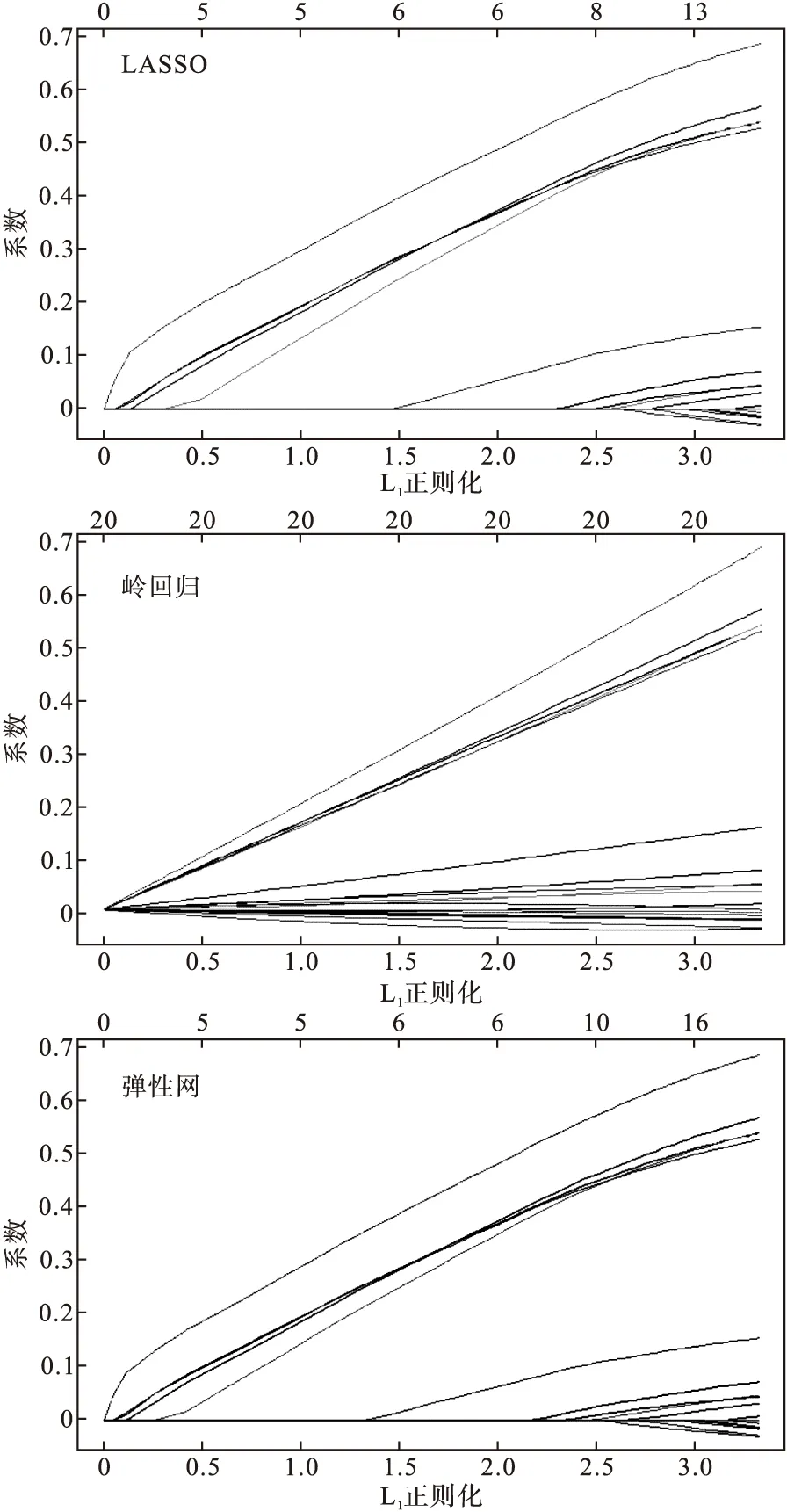
圖1　參數估計變化趨勢圖

圖2為分別擬合LASSO，嶺估計和彈性網時取不同log(λ)時模型誤差的變化趨勢。其中左側虛線對應平均誤差最小時(最優模型)的log(λ)(lambda.min)，右側另一條虛線是其1倍SE時對應的log(λ)(lambda.1se)，對應更簡潔的模型；圖形上方數字為模型對應的變量個數。本例中LASSO和彈性網各模型平均誤差接近，而嶺估計較高。如基于LASSO懲罰回歸，由于lambda.min和lambda.1se 對應的模型誤差變化不大，更偏好簡潔模型時，選擇lambda.1se對應的模型，此時λ值為0.0255，交叉驗證模型的平均誤差為1.3558。

選擇適宜的λ后，可提取最終模型參數估計的結果，包括回歸系數(beta)，自由度(df)，λ和決定系數R2(dev.ratio)等；其中決定系數是評判自變量對因變量解釋程度的重要指標，可進行模型之間的比較，具體程序為：

link_cv.best <-link_cv$glmnet.fit#提取最佳模型

link_cv.coef <-coef(link_cv$glmnet.fit,s=link_cv$lambda.1se)#提取模型系數

link_cv.coef #輸出模型系數

R<-link_cv.best$dev.ratio[which(link_cv.best$lambda==link_cv$lambda.1se)]#輸出R2

圖2　交叉驗證λ和模型誤差的關系

根據以上的語句，可輸出模型最終參數估計結果及R2。本例中，調整glmnet函數和cv.glmnet函數內的alpha值依次為1,0.5,0，分別對連鎖平衡數據和連鎖不平衡數據擬合LASSO、彈性網和嶺估計，各模型參數估計值及R2值如表2所示。

表2　連鎖平衡與連鎖不平衡數據擬合模型的參數估計值及R2

由表2可得，本例中，對連鎖平衡和連鎖不平衡數據，LASSO均給出稀疏解，較好地選擇有關聯SNPs而剔除無關聯變量；除關聯SNPs外，彈性網多保留一個無關聯SNP；而嶺估計因無法把參數壓縮為0，所有變量都保留在模型中，模型的復雜度高，但解釋度未增加。

討　　論

由于生物學測序技術的迅猛發展，遺傳關聯數據趨于高維，需要處理的信息量越來越大且存在大量的冗余信息和噪音，選擇顯著變量、擬合較簡單卻解釋程度好的模型是研究者面臨的共同問題，相應的統計分析方法也越來越被關注。基于懲罰的廣義線性模型在處理共線性，降維以及變量選擇方面有著獨特的優勢，在各類科研領域尤其是遺傳流行病學研究中的應用也隨之逐步興盛起來[3]。本文以遺傳關聯分析中常用的病例對照設計模擬數據為例，擬合LASSO，嶺估計和彈性網三種懲罰模型，運用glmnet包進行關聯性SNPs位點選擇，說明懲罰模型在遺傳關聯分析中應用的可行性及科學性。

實例分析可見，嶺估計能夠有效克服自變量間的高度相關，得到穩定的模型，但是它沒有稀疏性，不能有效地篩選自變量；但有研究表明，在嶺估計基礎上引入“Boosting”后可得到與LASSO同樣的估計，實現篩選變量的目的[11]。LASSO即L1懲罰可很好地降低維度，輕微解決共線性問題，但也有研究表明，LASSO有時可能過度壓縮參數[6]。彈性網對系數的懲罰介于嶺估計與LASSO之間，在本例結果中的表現更接近LASSO，且和LASSO一樣能同時進行模型選擇和參數估計。以往研究顯示，彈性網一般不會過度壓縮參數，能有效處理組群效應(group effect)，特別是能直接處理變量數遠遠大于樣本數的問題，這些是LASSO所不能達到的[12]。因此在實際分析中，還需根據具體情況選擇適宜的方法，如自變量弱共線時可考慮LASSO，強共線、高維小樣本數據時傾向于彈性網。本研究為便于說明R軟件結果，只采用了單個模擬數據集，無法體現懲罰模型更進一步的性質，如不同樣本量和連鎖不平衡參數時參數估計的準確度、混雜無關聯變異比例對變量選擇的影響等；更深入研究和比較各種懲罰方法，還需設置更多遺傳情境的模擬研究和實例應用。

glmnet包作為R數據挖掘中的三駕馬車之一，過程靈活，功能性強，可以擬合各類基于懲罰的廣義線性模型，通過最小化懲罰目標函數得到參數估計值。但是與一般的廣義線性模型不同，glmnet包無法直接計算Fisher信息陣進而估計參數的方差。有研究者提出可采用bootstrap方法計算估計值的標準誤[6]，或采用Bayesian LASSO獲得有效的β及標準誤[13]。還有學者提出可在似然比中設定“三明治”(sandwich formula)用于協方差估計[14]，這些方法及應用程序將進一步補充和完善glmnet包的功能。此外，在研究SNPs與疾病預后常用的生存時間資料時，glmnet包還可擬合基于三種懲罰的Cox模型。除此之外，R中還有許多其他擬合LASSO的相關軟件包：如較早時基于最小角回歸擬合傳統線性模型的lars；運用同倫算法擬合廣義線性模型的LASSO 2；還有和glmnet類似的penalized，也可選擇L1，L2或彈性網懲罰擬合各種廣義線性模型；而基于LARS-EN算法的elasticnet可以進行彈性網懲罰，能夠估計稀疏主成分。實際應用中，研究者可結合數據特征和實際需求加以選擇。

總之，運用R對高維數據建模時，懲罰廣義線性模型克服了傳統線性模型存在的預測精度和模型解釋度較差的缺陷，基于懲罰的變量選擇方法能夠在選擇變量的同時得到參數估計，加之計算量小，因此在處理高維數據時，有著傳統變量選擇方法無可比擬的優越性[15]。相信隨著懲罰廣義線性模型及軟件的推廣使用，它將在高通量遺傳關聯分析中發揮極其重要的作用。

[1]Ayers KL,Cordell HJ.Analysis of Genetic Analysis Workshop 18 data with gene-based penalized regression.BioMed Central Ltd,2014,S43.

[2]Zhang Z,Ersoz E,Lai C,et al.Mixed linear model approach adapted for genome-wide association studies.Nature genetics,2010,42(4):355-360.

[3]龔建朝.Lasso及其相關方法在廣義線性模型模型選擇中的應用.中南大學,2008.

[4]馬文浩.各種L_q懲罰在變量選擇中的應用及其比較.山東大學,2012.

[5]Hoerl AE,Kennard RW.Ridge Regression:Biased Estimation for Nonorthogonal Problems.Technometrics,1970(12):55-67.

[6]Tibshirani R.Regression shrinkage and selection via the lasso.Journal of the Royal Statistical Society.Series B(Methodological),1996:267-288.

[7]Zou H,Hastie T.Regularization and variable selection via the elastic net.J R Statist,2005(67):301-320.

[8]Friedman J,Hastie T,Simon N,et al.glmnet:Lasso and elastic-net regularized generalized linear models.CRAN，2009.

[9]Friedman J,Hastie T,Tibshirani R.Regularization paths for generalized linear models via coordinate descent.Journal of Statistical Software,2009,33(1):1-22.

[10]梁融.稀有變異關聯性分析中折疊與非折疊法的模擬比較研究.廣東藥學院,2014.

[11]Tutz G,Binder H.Boosting ridge regression.Computational Statistics & Data Analysis,2007,51(12):6044-6059.

[12]Bhlmann P,Sara VDG.Statistics for high-dimensional data:methods,theory and applications.Springer Science & Business Media,2011.

[13]Casella TPG.The Bayesian Lasso.Journal of the American Statistical Association,2008,103(482):681-686.

[14]Fan J,Li R.Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties.Journal of the American Statistical Association,2001,96(456):1348-1360.

[15]張秀秀,王慧,田雙雙,等.高維數據回歸分析中基于LASSO的自變量選擇.中國衛生統計,2013,30(6):922-926.

(責任編輯：鄧妍)

Application of Penalized Generalized Linear Model in Genetic Association Study and its Software Implementation in R

Zhang Junguo,Liu Li,Li Lixia,et al

(Department of Epidemiology and Biostatistics,School of Public Health,Guangdong Pharmaceutical University(510310),Guangzhou)

ObjectiveWith the development of high-dimensional data in genetic association studies,this study was aimed to depict the application of penalized generalized linear model based on ridge,LASSO and elastic net in genetic association study and its software implementation.MethodsWe introduced the penalized generalized linear model in detail,and performed the analyses in the simulated SNPs data in linkage equilibrium and linkage disequilibrium,respectively.At last,we used the ‘glmnet’ package in R software to fit the penalized generalized linear model with the example of logistic model.ResultsFor both of the SNPs data in linkage equilibrium and linkage disequilibrium,LASSO and elastic net could worked out sparse solution and effectively detected out the associated SNPs,as well as fairly excluded the non-associated variables.By contrast,the ridge model included all variables,and thus promoted the complexity of model,but meanwhile its explanation was not added.ConclusionFor the high-dimensional association data,LASSO and Elastic net can achieve effective dimensionality reduction,variables selection,and parameters estimation simultaneously,and thus reduce the complexity of the model.R glmnet package can flexibly fit different types of generalized linear model.Therefore,it can be wildly used in high-throughput genetic association studies.

Penalized generalized linear model;Genetic association studies;LASSO;Elastic net;Glmnet package

國家自然科學基金(81302493)；廣東省科技廳社會發展基金(2014A020212307)；廣東省自然科學基金(S2013040013590)

郜艷暉，E-mail:gao_yanhui@163.com