當均勻帶電體是什么形狀時在帶電體上某點有最大場強

姜付錦　吳 珊

(武漢市黃陂區第一中學　湖北 武漢　430300)

?

當均勻帶電體是什么形狀時在帶電體上某點有最大場強

姜付錦吳 珊

(武漢市黃陂區第一中學湖北 武漢430300)

先用“對稱性原理”對均勻帶電體在表面某點產生最大電場強度時的形狀進行了定性分析，然后用變分學的歐拉方程對物體的形狀進行定量研究，最后對這個問題進行歸納和總結.

對稱性原理歐拉方程泛函

一個均勻帶電體的電荷量是一定的，若帶電體是一均勻帶電直線，則當直線彎成什么形狀時在曲線上某一點產生的電場強度最大呢？若帶電體是二維平面，則當帶電平面是什么形狀時在平面邊緣某一點產生的電場強度最大呢？若帶電體是三維立體結構，則當帶電體表面是什么形狀時在表面某一點產生的電場強度最大呢？它們會是圓形或球形嗎？這其實是個泛函問題，本文先對物體形狀作定性分析再對形狀進行定量計算．

1　物體形狀的定性討論

如圖1所示，以物體上某一點為原點O，豎直向上的方向為極軸，建立球坐標系(r,θ,φ)，其中r∈[0,∞),θ∈[0,π],φ∈[0,2π]，則物體上的任意一點可由坐標(r,θ,φ)確定，物體表面可由函數r=R(θ,φ)描述．要使原點處的電場強度最大，物體的形狀應具有以下特性：

(2)物體形狀具有旋轉對稱性，繞極軸旋轉任意角度對稱，故物體表面函數簡化為r=R(θ)．由“對稱性原理”[1]：原因中的對稱性必反映在結果中，即結果中的對稱性至少有原因中對稱性那樣多．

圖1　物體形狀的定性討論

2　物體形狀求解的一般方法

滿足固定邊界條件y(x0)=y0,y(x1)=y1的光滑函數集合中，求一個函數y=y(x)，滿足條件(等周條件)

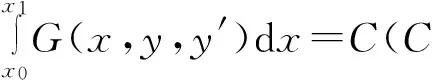
并使

2．1當帶電體是三維物體時的形狀[3]

設電荷連續分布的物體的電量為Q，電荷的體密度為ρ且保持不變，在球坐標系中物體的體積可以表示為

電場強度表達式為

由于物體具有旋轉對稱性，帶電體在原點處產生的電場強度在垂直于極軸方向上的分量為零，物體在原點產生的電場強度為

令t=cosθ,R1(cosθ)=R(θ)，則

由上述的方法知

得

由等周條件得

圖2　帶電體的三維結構圖

2．2當帶電物體是二維平面時的形狀

設電荷連續分布的物體的電荷量為Q，面密度為σ且保持不變，在極坐標系中物體的面積可以表示為

原點處的電場強度為

若令

t=cosθR1(cosθ)=R(θ)

則等周條件為

電場強度為

由上述的方法可知

得

即

由等周條件得

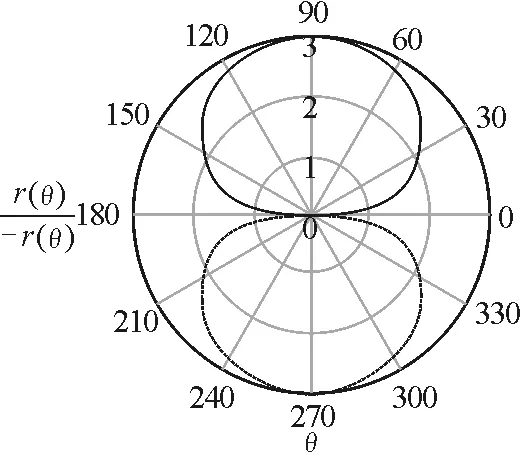
圖3　帶電體的二維平面的形狀

2．3當帶電體是一條粗細均勻曲線時的形狀

設電荷連續分布的物體的電荷量為Q，線密度為λ且保持不變，物體的長度可以表示為

由等周條件得

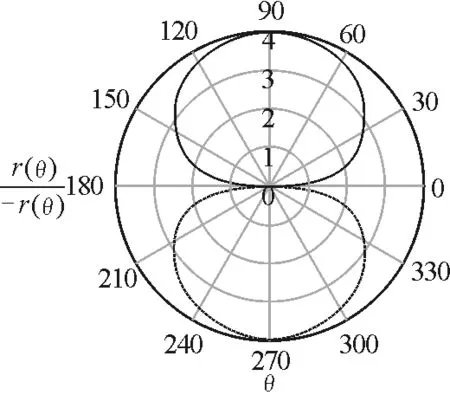
圖4　帶電體是彎曲線時的形狀

3　結語

通過對帶電體的3種情況分析可以發現：

(1)物體的形狀具有旋轉對稱性；

(2)物體上每個微元電荷在表面某一點產生的電場強度沿極軸方向上的分量相同；

(3)物體表面的形狀可以表示為R(θ)=

1趙凱華.定性與半定量物理學．北京：高等教育出版社，1991.33

2歐斐君.變分法及期應用：物理、力學、工程中的經典建模．北京：高等教育出版社，2013.47～65

3楊星宇.力學中一個趣味問題的討論．物理通報，2015(8)：57～59

4史友進，俞曉明.庫侖摩擦最速降曲線問題的討論．鹽城工學院學報(自然科學版)，2012(6)

5史友進，俞曉明.庫侖摩擦因數對串珠經典速降線與改進速降線下滑影響．牡丹江大學學報,2011(7)

2016-01-07)