質點沿豎直光滑曲線運動時脫離約束點研究

田寶國　吳世永　宿德志

(海軍航空工程學院基礎部　山東 煙臺　264001)

?

質點沿豎直光滑曲線運動時脫離約束點研究

田寶國吳世永宿德志

(海軍航空工程學院基礎部山東 煙臺264001)

利用質點運動動力學方程和機械能守恒定律，對質點在豎直平面內沿任意光滑曲線運動時脫離曲線的條件進行了研究，根據曲線方程的不同形式給出了質點脫離約束時的一般公式，并通過具體實例進行了驗證．

光滑曲線脫離約束牛頓運動定律

在質點沿豎直平面內光滑曲線自由下滑過程中，如果在某處質點所受的支持力為零，則質點就會脫離曲線的約束而運動．在一些教材中，主要針對曲線為圓和拋物線的情況進行了討論[1，2]．本文利用質點運動的動力學方程和機械能守恒定律以及各種曲線方程的曲率半徑公式，推導出了質點在豎直平面內沿任意光滑曲線自由下滑時脫離曲線約束的一般結論，給出了在各種曲線方程形式下質點脫離曲線時的一般公式，并借此對圓、拋物線、正弦曲線等具體曲線的例子進行了研究．

1　質點脫離曲線的一般公式

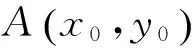
(1)

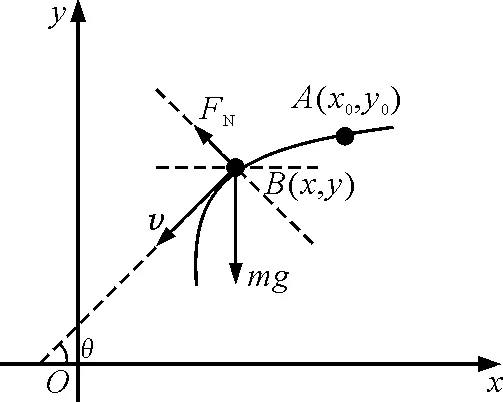
圖1

其中，ρ為曲線在B點處的曲率半徑．當質點脫離曲線約束時，FN=0，于是得

(2)

根據機械能守恒定律

(3)

由式(2)和式(3)得到

(4)

其中

(5)

下面根據不同曲線方程的形式給出質點脫離曲線約束時的一般表達式．

(1)若曲線方程為y=f(x)，則曲率半徑表達式為[3]

(6)

當物體能夠脫離約束，曲線必為凸曲線，即

y″<0，為保證曲率半徑為正，則

(7)

由式(4)、(6)、(7)可得此時脫離曲線約束時滿足的方程為

1+y′2=2(y-y0)y″

(8)

(9)

由式(4)、(6)、(9)可得此時脫離曲線約束時滿足的方程為

(10)

即

(11)

(12)

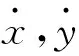
(13)

式(8)、(11)和(13)即為在不同曲線方程形式下質點脫離曲線約束時滿足的表達式．

2　應用舉例

(1)曲線為半徑為R的圓

圖2

若質點的軌跡方程為

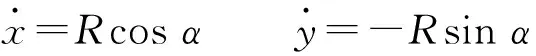
代入式(13)可得

3cosα=2

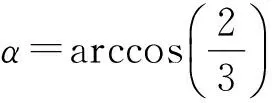
(2)橢圓

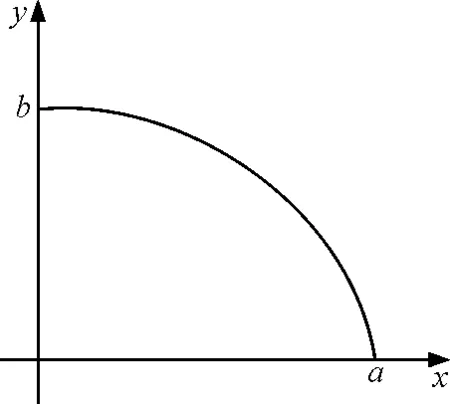
圖3

質點的軌跡方程為

設質點從最高點y0=b處由靜止下滑．由軌跡方程可得

代入式(11)可得方程

其根的判別式為

所以方程有一個實根和兩個復根，實根表達式即為質點下滑時脫離曲線的位置，根據一元三次代數方程求根卡爾丹公式[3]可得質點脫離曲線約束時的解為

(3)拋物線

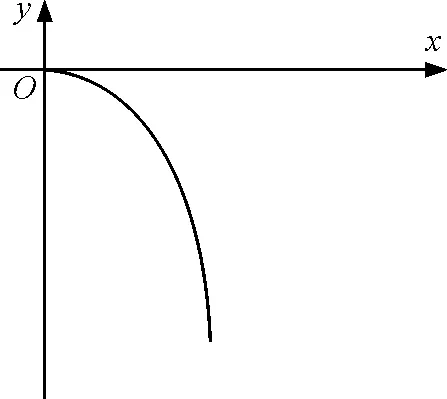
圖4

質點軌跡方程為

設質點從原點O由靜止開始下滑，由軌跡方程可得

y′=-2axy″=-2a

代入式(8)得到

2ax=0

因為x>0，所以方程無解，說明質點自由下滑過程中不會脫離該拋物線．

(4)正弦曲線

質點軌跡方程為

y=asinx

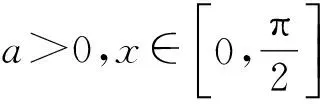
a2sin2x-2a2sinx+a2+1=0

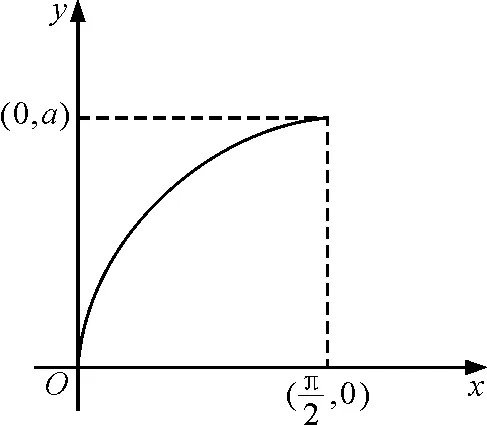
圖5

根據本文結論，可對任意形狀的平面曲線，如雙曲正弦線、普通擺線等進行研究，在此不再贅述．

1李書民. 經典力學概論.合肥：中國科學技術大學出版社, 2007.13～14

2周衍柏. 理論力學教程. 北京： 高等教育出版社, 2010.

73～74

3數學手冊編寫組.數學手冊.北京：高等教育出版社,2009.88,378

2015-03-23)