THE APPLICATION OF THE BASIN OF ATTRACTION TO THE EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR THE SECOND ORDER PARABOLIC BOUNDARY VALUE PROBLEM

FENG Yan-qing，WANG Zhong-ying

(School of Mathematics and Chemical Engineering，Changzhou Institute of Technology，Changzhou 213000，China）

THE APPLICATION OF THE BASIN OF ATTRACTION TO THE EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR THE SECOND ORDER PARABOLIC BOUNDARY VALUE PROBLEM

FENG Yan-qing，WANG Zhong-ying

(School of Mathematics and Chemical Engineering，Changzhou Institute of Technology，Changzhou 213000，China）

In this paper，a new sufficient condition of the existence and uniquence of the second order parabolic boundary value problem is given by using the basin of attraction and the comparison theorem，which generalize some existed theorems.

the basin of attraction；homeomorphism；initial value problem；the second order parabolic boundary value problem

2010 MR Subject Classification：35K20

Document code：AArticle ID：0255-7797（2016）05-0949-06

1 Introduction

We will study the parabolic operator

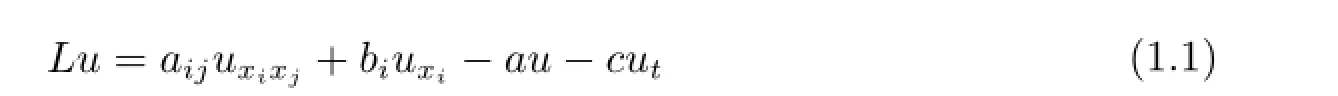
acting on functions in D=?×［0，T］，where aij（x，t）∈（D），bi，a∈L∞（D），c=c（x）∈（?）and ? is a connected bounded subset of n-dimensional space.

Using a continuous method，Sigillito exlpored the solution for the heat equation，see［1］. Elcart and Sigillito derived an explicit coercivity inequality‖|u|‖≤const‖Lau‖0and gave a sufficient condition for the existence and uniqueness of solution to the the second order parabolic，see［2］.

Recently，in this area，the global diffeomorphism theorem was used to prove the existence and uniqueness of solutions of nonlinear differential equation of certain classes.In addition，many authors were extensively investigated this problem，see Mayer［3］，Plastock ［4］，Radulescu and Radulescu［5］，Shen Zuhe［6-7］，Zampieri［8］.These theorems may be used for solving nonlinear systems of equation.

Motivated by these results，we shall utilize an interesting tool，the attraction basin to give a new set of sufficient condition for the existence and uniqueness of the second order parabolic boundary value problems in this paper，which can be founded in Section 3.Using our approach it is easy to obtain results of Elcart and Sigillito.Moreover，the methods apply not only to this problem but also to other nonlinear diffierential equations.

2 Preliminaries

In this section，we will state some lemmas which are useful to our results.First，we introduce the basin of attraction.

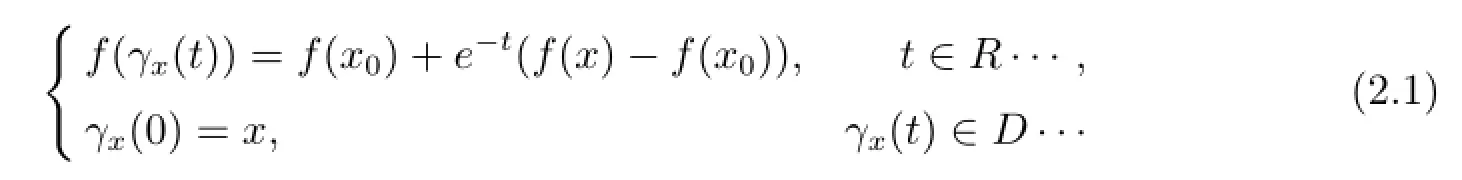
Lemma 2.1（see［8］）Let G，F be Banach spaces，D be an open subset of G，x0∈D and f：D?G→F be a C1mapping and a local homeomorphism.Then for any x∈D，the path-lifting problem has a unique continuous solution t→γx（t）defined on the maximal open interval Ix= （tx-，tx+），-∞≤tx-，tx+≤+∞.Moreover，the set｛（x，t）∈D×R：t∈Ix｝is open in D×R and the mapping is（x，t）→γx（t）continuous.

Definition 2.1［8］In the setting of Lemma 2.1，the basin of attraction of x0is the set

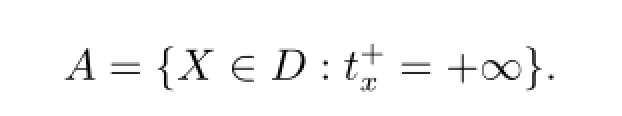
Theorem 2.1［9］With the above setting，f is a global homeomorphism onto Y if and only if γx（t）is defined on R for all x∈A，namely，γx（t）can also be extended to-∞.

Lemma 2.2（see［8］）Let X be Banach space，a，b∈R and p：［a，b］→X be a C1mapping on［a，b］.Then‖p（t）‖has derivative‖p（t）‖＇almost everywhere and‖p（t）‖＇≤‖p（t）‖for a＜t＜b.

Second，the following comparison theorem play an important role to prove the sufficient condition for the existence of a unique solution of problem（1.1）.

Let E be an open（t，x）-set in R2and g∈C［E，R］.Consider the scalar differential equation with an initial condition

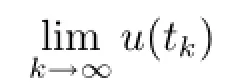
Theorem 2.2（Comparison theorem in［9］）With the above setting，suppose that［t0，t0+ b）is the largest interval in which the maximal solution r（t）of（2.2）exists.Let

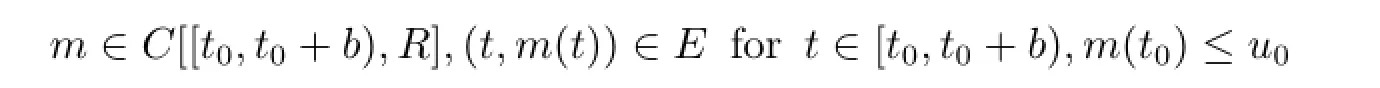
and for a fixed Dini derivative

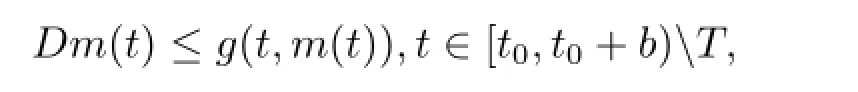
where T denotes an almost countable subset of t∈［t0，t0+b）T，then

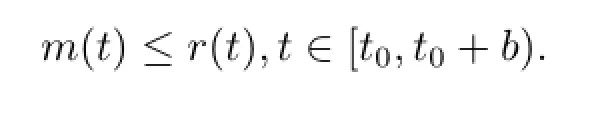
3 Existence Theorem

Consider the boundary value problem

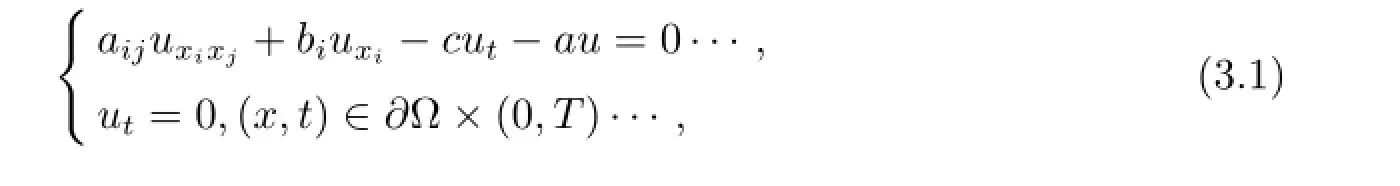
where ut∈L2（［0，T］（?））.Let W0（D）denote the Hilbert space with the norm

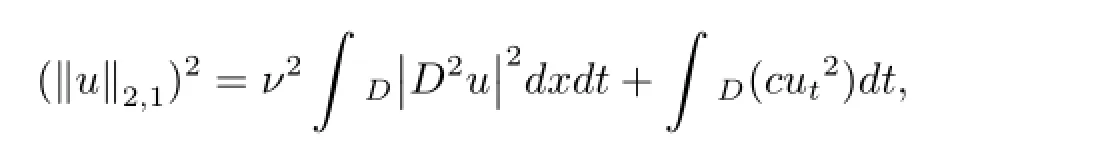
where|D2u|2represents the sum of the a squares of all the second derivatives with respect to space variables and ν is positive constant.

The following assumptions are needed later.

A1 The boundary of ? is piecewise smooth with nonnegative mean curvature everywhere.

A2 f：W0（D）→L2（D）is continuous and a bounded function of t，x1，···，xn，u.

Elcart and Sigillito gave the following inequality in［2］.

Lemma 3.1If u∈W0，then

where

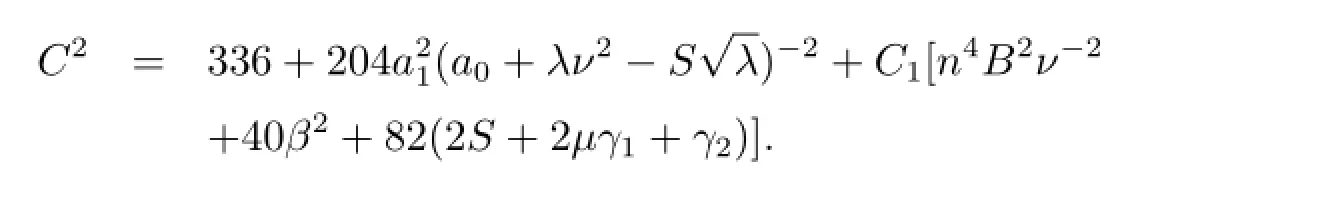
Denote Mu=aijuxixj+biuxi-cut，then M is the linear operator from W0（D）to L2（D）. We may express（3.1）in the form

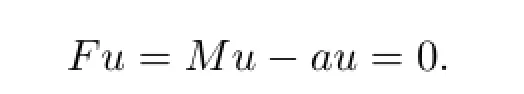
For u，φ∈W0（D），we have

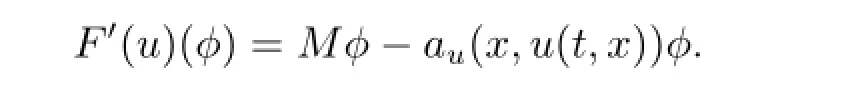
Define

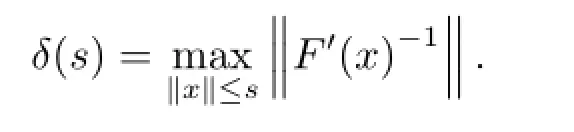
Theorem 3.1In the setting of the above，equation（1.1）exists a unique solution if the following conditions hold

（2）for each，the maximum solution of the initial value problem

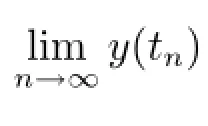
ProofWe have from（2.1）and Lemma 2.2 that

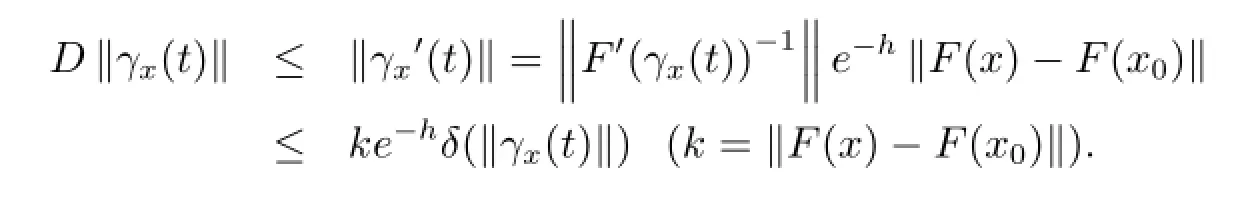
By assumption A2，we know the maximum solution y（t）of（3.3）is defined on［0，c）and there exists a sequence tn→c as n→∞such that

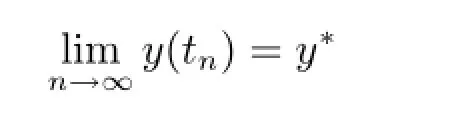
is finite.It follows that y（t）is continuous on［0，c）and there is a constant M such that

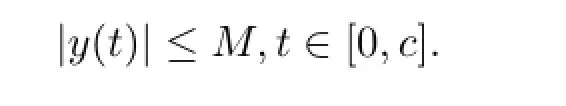
By the comparison theorem，we have

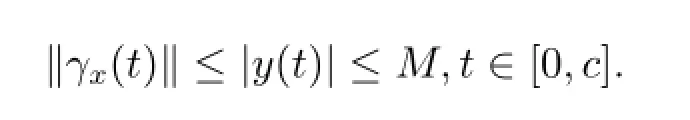
From conditions A1，A2 and condition（1），since λ=inf0 is the lowest eigenvalue of-Δ in ?，it follows that for all u∈W0（D），zero is not an eigenvalue ofMφ-au（x，u（t，x））φ，so for every u∈W0（D），the operator F＇（u）=M-auI is invertible and F is a local homeomorphism from W0（D）onto L2（D），where I denotes the identical operator.

Then in view of Theorem 2.1，we need only show that for all x∈A，γx（t）can also be extended to-∞，namely，we need consider the problem in the opposite direction.

Let g（-h）=γx（t），t∈（a，0］，h∈［0，-a），a＜0 for t1，t2∈（a，0］，we have

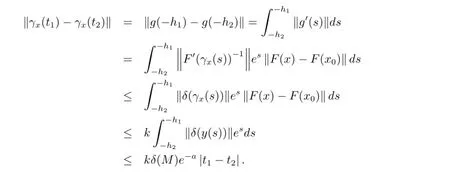
So γx（t）is Lipschitz continuous on（-a，0］，γx（t）can also be extended to-∞，the theorem is proved.

Elcart and Sigillito［2］studied the following initial-boundary value problem

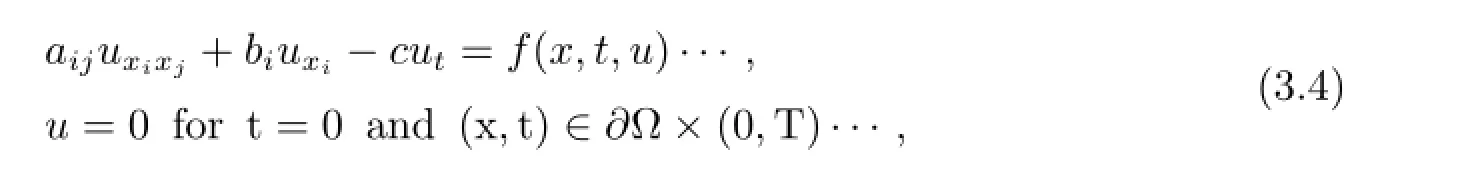
where??∈C2and f is continuous and has three derivatives with respect to u.Problem （3.4）may be formulated as an operator equation Pu=0，where Pu=Mu-f（x，u）is a mapping of W0（D）onto L2（D）.

Corollary 3.1 Assume that f satisfies

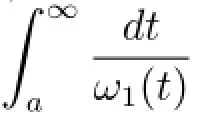
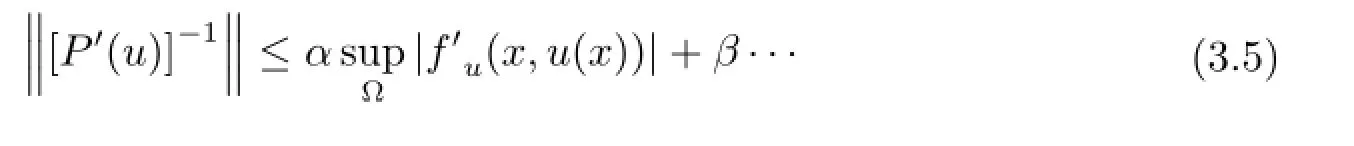
for positive constant α，β，then δ（t）≤ω1（t），and thus

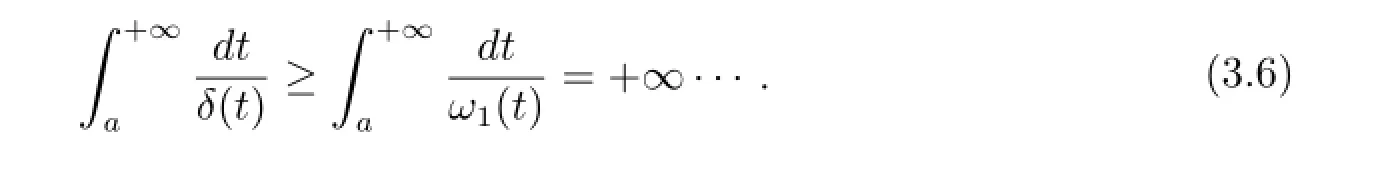
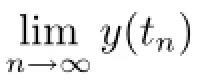
RemarkCondition（ii）in Corollary 3.1 can be replaced with=O（u），because=∞holds.The result of Elcart and Sigillito in［2］becomes a special case of Theorem 3.1.

References

［1］Sigillito V G.On a continuous method for approximating solution of the heat equation［J］.Assoc. Comp.Mach.，1967，14（5）：732-741.

［2］Elcrat A R，Sigillito V G.An explicit a priori estimate for parabolic equations with applications to semilinear equations［J］.J.Math.Anal.Appl.，1976，7（5）：746-753.

［3］Meyer G H.On solving nonlinear eauations with a one-parameter operator imbedding［J］.SIAM.J. Numer.Anal.，1968，5（5）：739-752.

［4］Plastock R.Homeomorphism between Banach space［J］.Trans.Amer.Math.Soc.，1974，200（3）：169-183.

［5］Elcrat A R，Sigillito V G.Coercivity for a third order Pseudoparabolic operator with applications to semilinear equations［J］.J.Math.Anal.，1977，61（3）：841-849.

［6］Shen Z H.On the periodic solution to the Newtonian equation of motion［J］.Nonl.Anal.，1989，13（2）：145-149.

［7］Shen Z H，Wolfe M A.On the existence of periodic solution of periodically perturbed conservative systems［J］.Math.Anal.Appl.，1990，153（1）：78-83.

［8］Zampieri G.Diffeomorphisms with Banach space domains［J］.Nonl.Anal.，1992，19（10）：923-932.

［9］Lakshmikantham V，Leeda S.Differential and integral inequalities Vol.II［M］.New York：Academic Press，1969.

［10］Feng Y Q，Wang Z Y.Global homeomorphism and the existence of solutions for periodically perturbed conservative systems［J］.J.Nanjing Univ.Math.Biqu.，2011，28（1）：24-32.

［11］Cai Xinmin.Coupled fixed point theorem for a kind of nonlinear operators［J］.J.Math.，2002，22（2）：162-164.

吸引盆在二階拋物線邊值問題解存在唯一性中的應用

馮艷青，王忠英
（常州工學院數理與化工學院，江蘇常州213000）

本文研究了二階拋物線邊值問題解的存在唯一性的問題.利用吸引盆的方法和全局同胚理論，推導出二階拋物線邊值問題解存在唯一性的一個充分條件，從而推廣了已經存在的一些定理.

吸引盆；全局同胚；初值問題；二階拋物線邊值問題

MR（2010）主題分類號：35K20O175.26

date：2014-04-14Accepted date：2015-01-04

Supported by the Natural Science Foundation of JiangSu（13KJD110001）.

Biography：Feng Yanqing（1969-），female，born at Yiwu，Zhejiang，associate professor，major in nonlinear function analysis and application.