二維不可壓縮Navier-Stokes方程的七模類Lorenz方程組的動力學行為及其數值模擬

王賀元

（遼寧工業大學理學院，遼寧錦州121001）

二維不可壓縮Navier-Stokes方程的七模類Lorenz方程組的動力學行為及其數值模擬

王賀元

（遼寧工業大學理學院，遼寧錦州121001）

本文研究了平面不可壓縮的Navier-Stokes方程一個七模類Lorenz方程組的混沌行為問題.利用模式截斷的方法，獲得了一個七模類Lorenz方程組，證明了該方程組吸引子的存在性，并對其全局穩定性進行了分析和討論.基于分岔圖、最大李雅普諾夫指數、龐加萊截面、功率譜揭示了系統混沌行為的普適特征，仿真分析了系統動力學行為的演化過程.

Navier-Stokes方程；奇怪吸引子；李雅普諾夫函數

1　引言

流動現象是自然界及人類生產科研活動中最為常見的一種物理現象，流動穩定性是流動現象最為關鍵的問題.作為流動現象應普遍遵循的Navier-Stokes方程是一種典型的非線性偏微分方程，刻劃著流體的運動規律，如大氣運動、海洋流動、軸承潤滑、透平機械內部流動等，研究它對人們認識和控制湍流至關重要.1963年美國氣象學家E.Lorenz在研究大氣對流時，首次給出了著名的Lorenz方程［9］.所采用的方法是對Navier-Stokes方程和熱傳導方程進行傅立葉級數展開，截取級數的前三項，得到三模的Lorenz系統.20世紀后期Valter Franceschini又在此方向上進一步擴展，多次和其他學者合作，將二維正方形區域T2=［0，2π］×［0，2π］上不可壓縮的Navier-Stokes方程

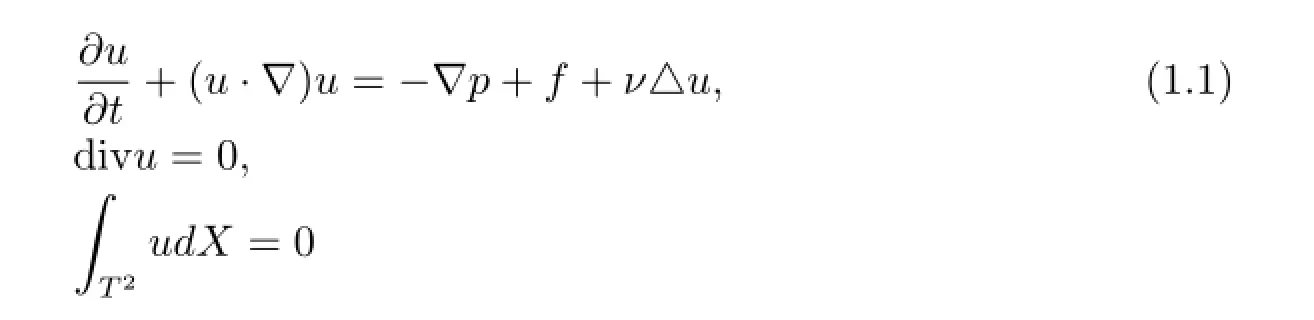
（其中u為速度場函數；p為液體之間的壓力；f為外力場函數，ν為動力粘性系數）進行傅立葉展開并截取其中的有限項，得出五模和七模或者任意模的非線性微分方程組（見文獻［1-4］），討論當雷諾數變化時方程組解的動力學行為.這種截斷后來被擴展到三維空間，1988 年V.Franceschini，Inglese和Tebaldi在Commun.Mech.Phys.上發表了三維空間上的有關Navier-Stokes方程五模截斷的文章［7］；1991年Franceschini和Zanasi在三維空間上對此方程傅立葉展開，進行七模截斷后得到十四個非線性微分方程組成的方程組，隨后又對這個復雜的方程組進行了詳細的討論［3］.國內王賀元等人選取不同的截斷模式，并把這方面的研究擴展到磁流體，得到相應類Lorenz方程組并分析了系統的動力學行為［10，11］.Franceschini 在1981年給出的一個七模類Lorenz方程組［1］，討論了這個七模模型定常解的線性穩定性，并對分歧行為進行了數值模擬.本文對此模型的動力學行為進行深入的分析和探討，證明了該模型吸引子的存在性，并討論了其全局穩定性，從而在理論上保證了數值模擬的有效性，并且數值模擬了分歧和混沌吸引子的發生過程.

2　七模類Lorenz方程組

下面對二維區域［0，2π］×［0，2π］上Navier-Stokes方程進行傅立葉展開.即對速度函數u，外力場函數f和流體之間的壓力p進行如下傅立葉展開

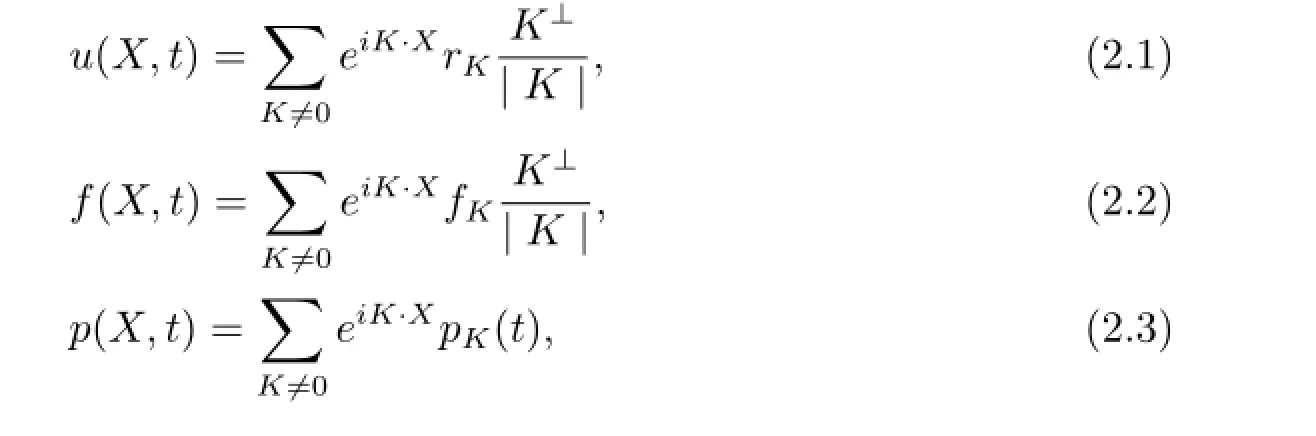
其中K=（h1，h2）是波向量，K⊥=（h2，-h1），rK=rK（t）為時間t的函數.將（2.1）-（2.3）式代入到方程組（1.1），經過一系列運算得到如下形式的微分方程組［1，2］

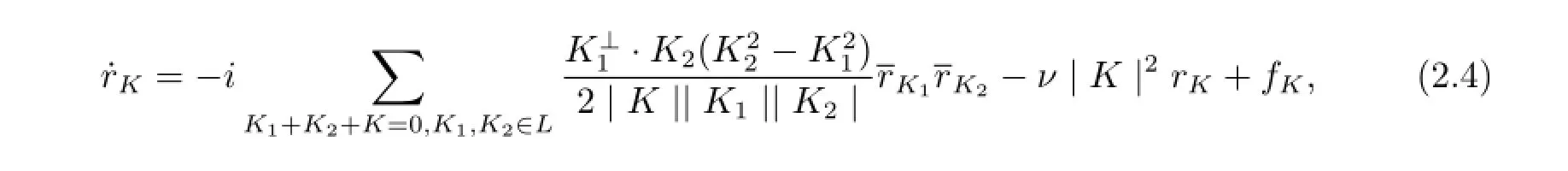
其中L為波向量集合，并且滿足若K∈L，則-K∈L.文獻［1］取

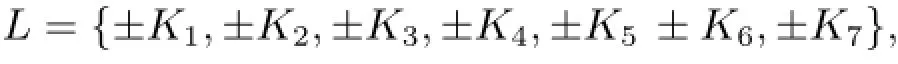
其中

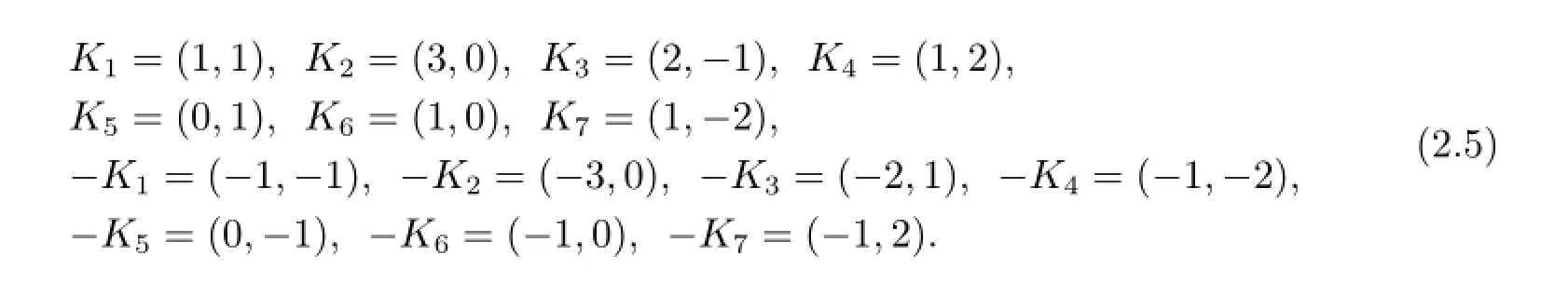
在ν=1時，分別令K為K1，K2，K3，K4，K5，K6，K7，代入到方程組（2.4）經大量計算，利用實條件作代換

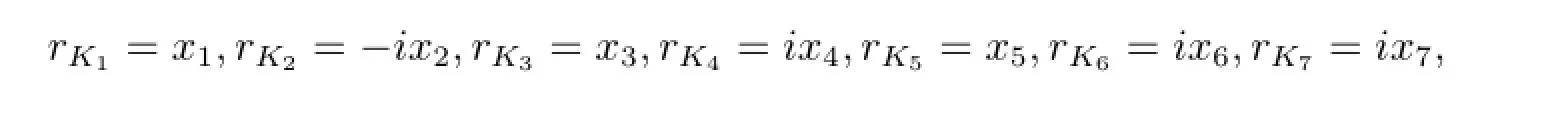
為

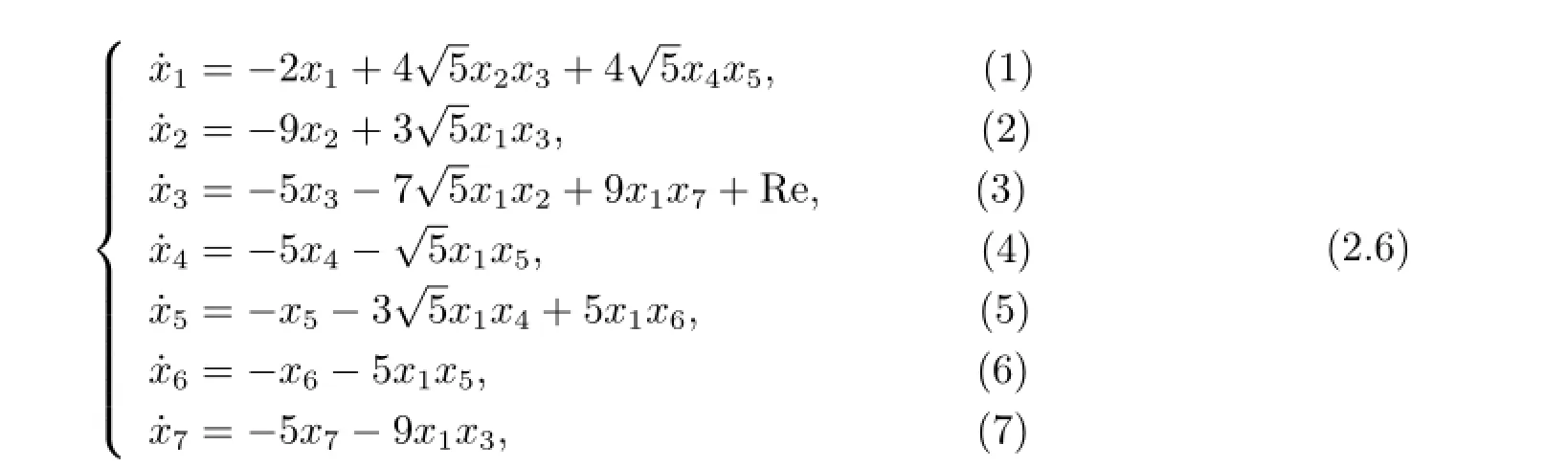
這里xi=xi（t）（i=1，2，···，7）為譜展開系數.截得了七模非線性微分方程組的形式和Lorenz方程組相似，稱其為類Lorenz系統.

3　平衡點及穩定性分析

由于系統（2.6）在平衡點處Jacobi矩陣與時間無關，故李雅普諾夫矩陣的特征指數就是Jacobi矩陣的特征值的實部［5，6］，它是刻畫吸引子性質的重要指標，尤其對混沌吸引子更為重要.下面對類Lorenz方程組（2.6）線性化，然后根據各個平衡點的李雅普諾夫矩陣的特征指數的變化來討論平衡點的穩定性.令

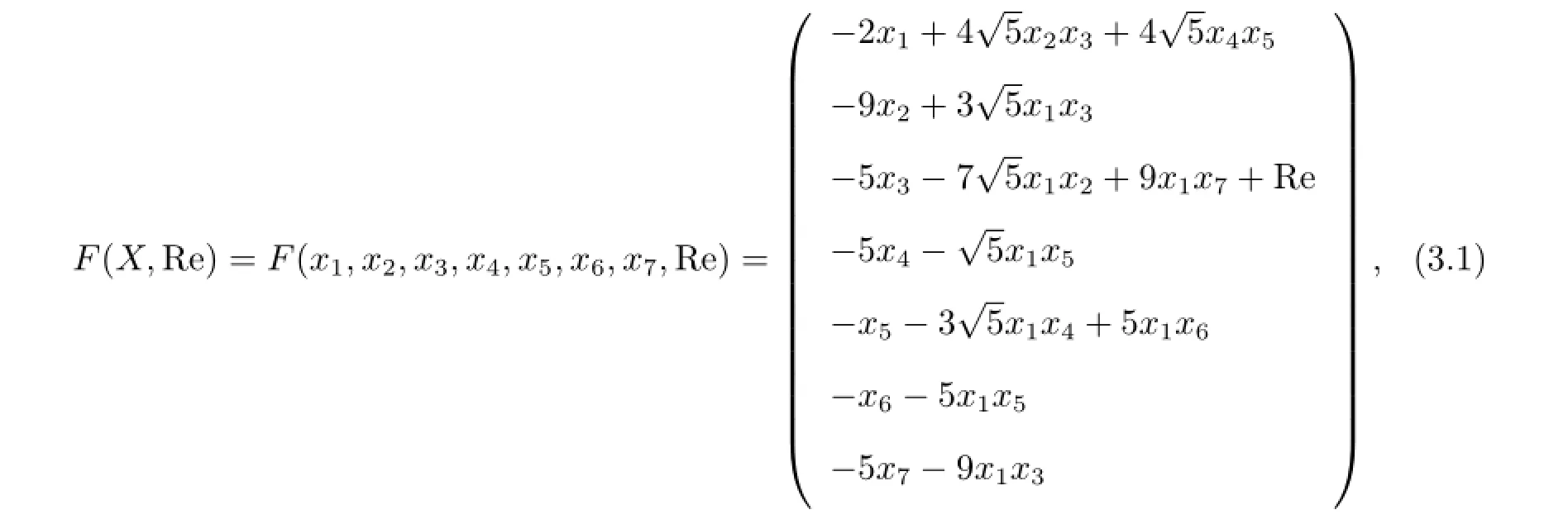
對F（X，Re）關于X求導數得到如下李雅普諾夫矩陣

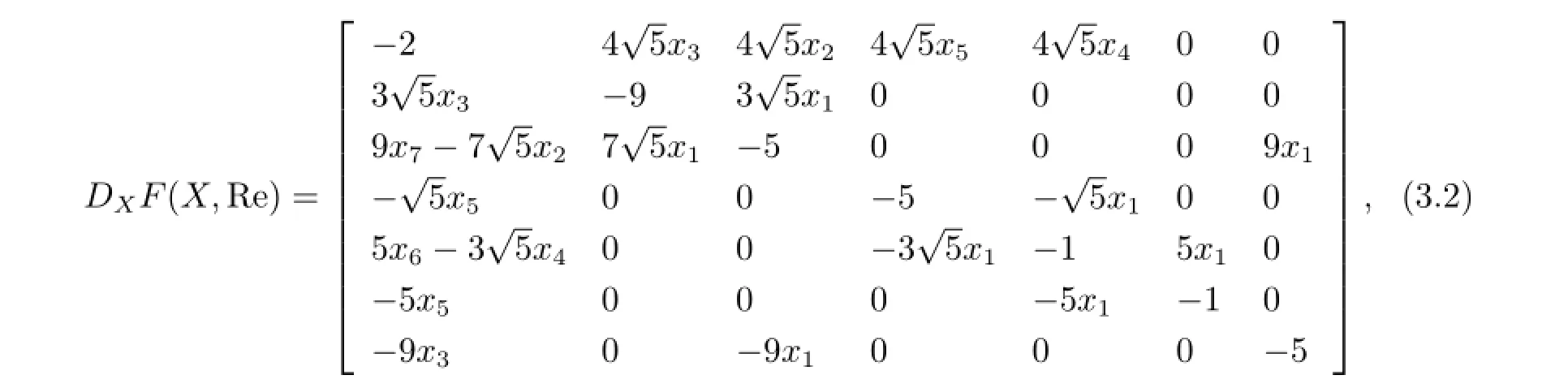
由F（X，Re）=0求出（2.6）式的平衡點，下面根據Liapunov矩陣的特征指數的變化情況討論各平衡點的穩定性（具體參見文獻［1］）.

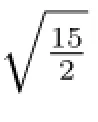
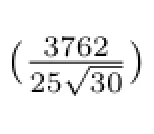
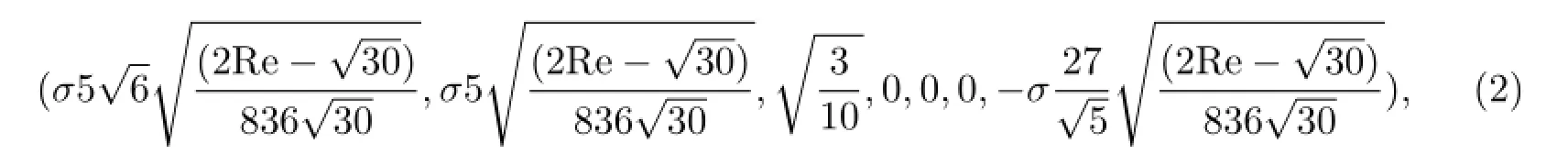
其中σ=±1，此時平衡點（1）變得不穩定，兩個新平衡點（2）是穩定的.

3）當Re＞R2時，所有平衡點（1），（2）都是不穩定的.

4　吸引子的存在性和全局穩定性分析

耗散動力系統的混沌行為是由于存在著一個復雜的吸引子而引起的［8］，而這個吸引子就是系統的所有軌道當時間趨于無窮時收斂到的集合，可能是一個分形或康托集或康托集和一個區間的乘積.很自然地這個“吸引子”就成為數學上用來描述觀察到的不穩定流的對象，它的復雜結構就是導致觀察到的混沌現象的原因.因此，研究吸引子的存在性和數值模擬就成為一個重要的問題.下面就來證明系統（2.6）的吸引子存在性.

取H=R7，u（t）=（x1，...，x7），對Navier-Stokes方程的七模類Lorenz方程組（2.6）作如下運算

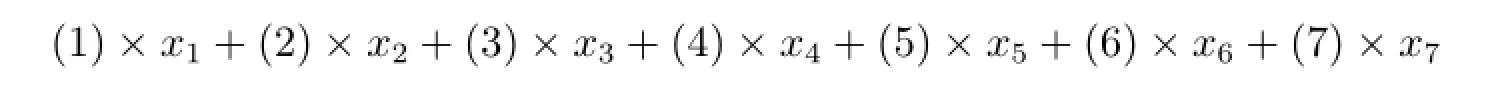
得

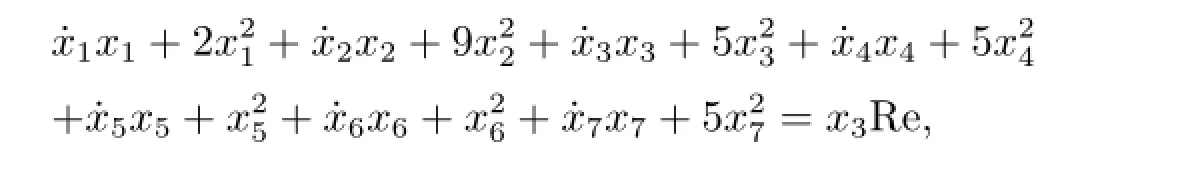
因此有

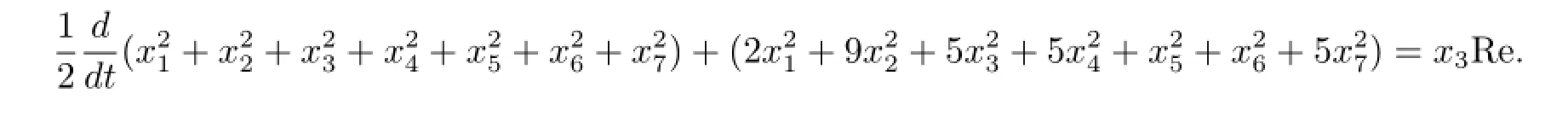
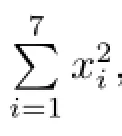
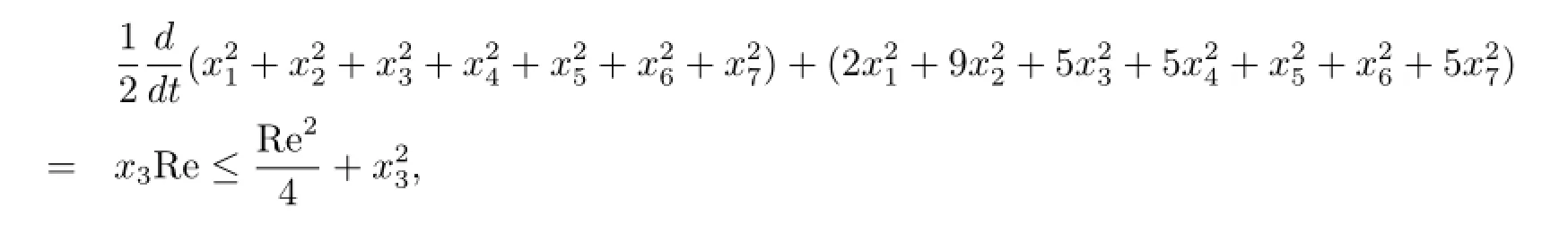
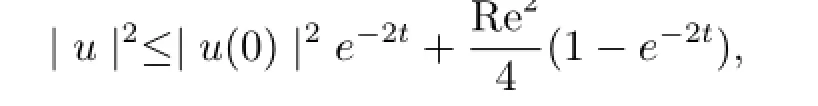
因此有

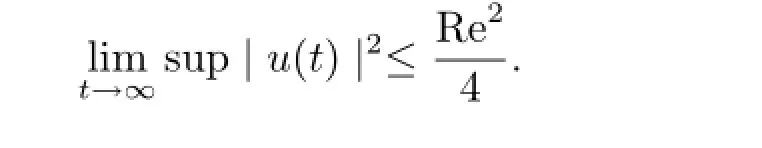
故有

非線性系統具有全局穩定性時，其軌線所收斂的單連通閉區域稱為系統的捕捉區.只要能證明捕捉區的存在，不論其中的定常解是否穩定，系統均具有全局穩定性.而研究系統的全局穩定性主要借助于李雅普諾夫函數方法［5，6］.李雅普諾夫函數方法的基本思想是構造一個函數，然后利用它的性質和這個函數沿方程（2.6）的軌線方向的全導數的性質以確定（2.6）式平衡點的穩定性，以確定系統的捕捉區.

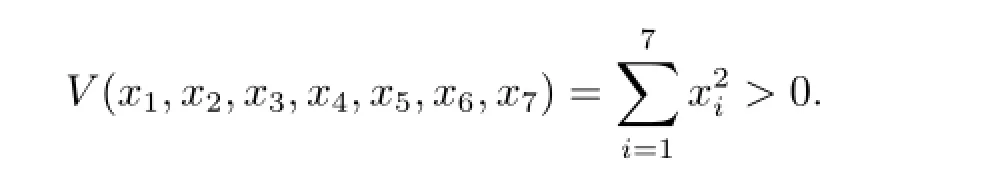
對系統（2.6）構造李雅普諾夫函數為令V（x1，x2，x3，x4，x5，x6，x7）=K，很明顯，當K是一正常數時，上式表示H上的一球面，記為E.求V的導數，并利用（2.6）式

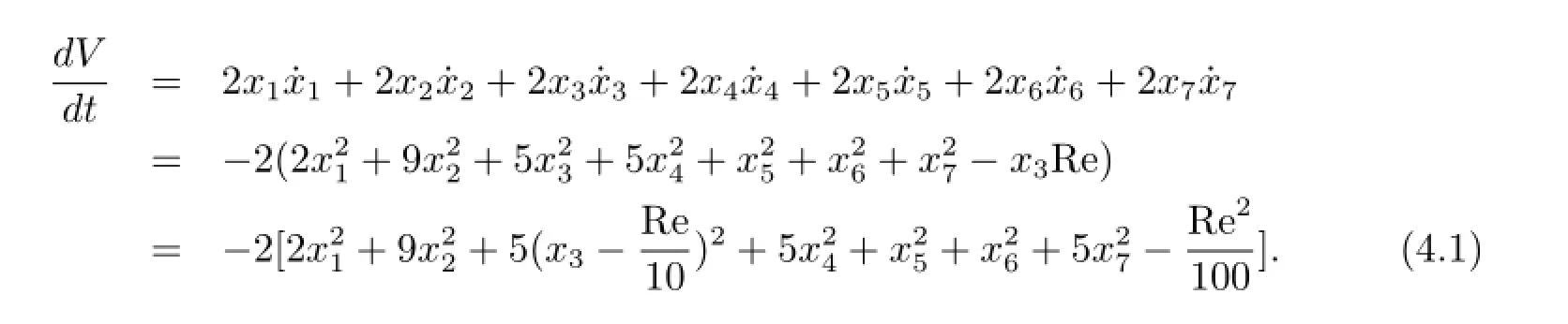
于是若把K取得充分大，E即可包圍C.這樣從式（4.1）式可知在C外面＜0，由李雅普諾夫定理［5］的分析得知E外（2.6）式的解軌線都將進入E內.可見E就是類Lorenz系統（2.6）的捕捉區.雖然這時系統平衡點（1），（2）都不穩定，但系統仍具有全局穩定性：系統最終要收縮到捕捉區內，而區內又無收點，因此系統只能在區內不停的振蕩.于是軌線最終要在捕捉區內形成一個不變集合，這就是所謂的吸引子.人們稱混沌運動這種具有獨特性質和結構的吸引子為奇怪吸引子.它是整體穩定性和局部不穩定性一對矛盾的結合體.其具體形式如何呢？下面就來數值模擬系統（2.6）的奇怪吸引子.

5　數值模擬

隨著雷諾數的增大，Lorenz方程組（2.6）的穩定性發生了變化，出現了Hopf分岔和混沌等非線性現象.下面就來詳細數值模擬系統（2.6）從分岔到混沌的全過程.

1）當Re＜R2=30.2123時，系統（2.6）的新平衡點是穩定的，解軌線為螺旋線（如圖1，2）.

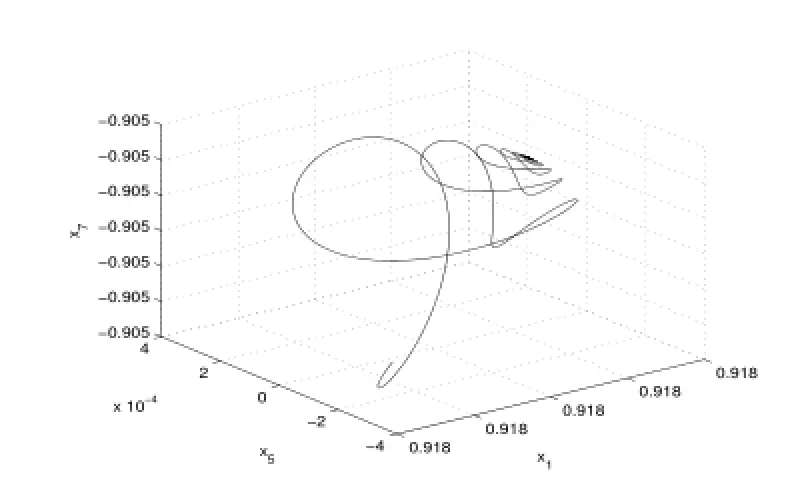
圖1：Re=15.60

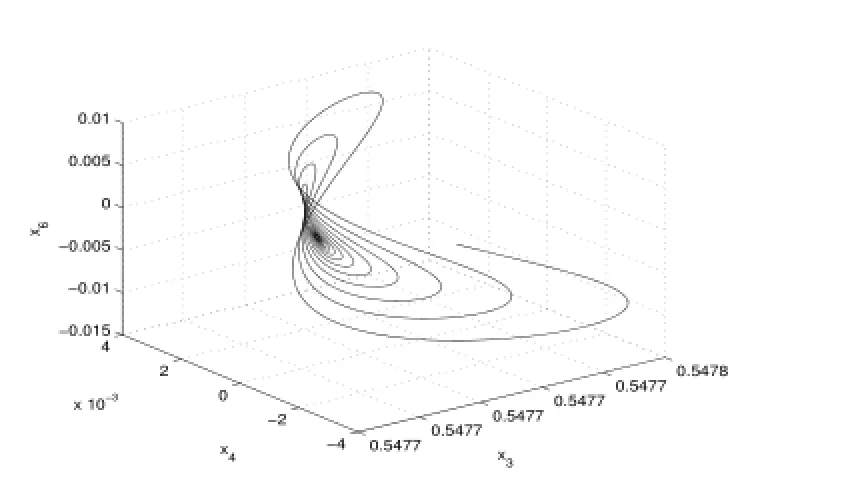
圖2：Re=20.04

2）通過數值計算得方程組（2.6）在Re=R2時平衡點p±處的李雅普諾夫矩陣的一對復共軛特征值穿越虛軸，其實部由負變正，因而系統（2.6）發生了Hopf分岔.從不穩定平衡點p±分叉出閉軌線.如圖3-6.

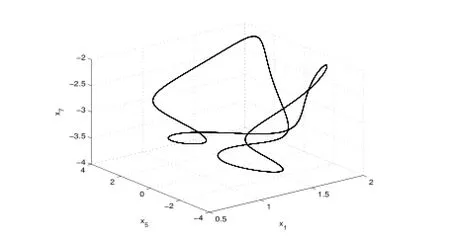
圖3：Re=30.2122

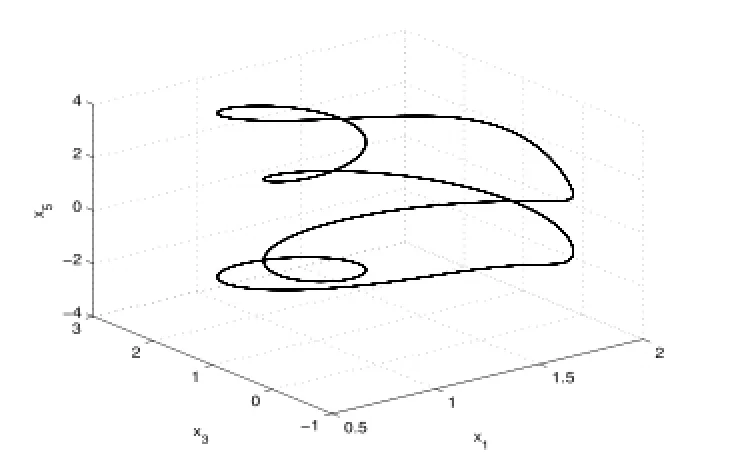
圖4：Re=30.2124

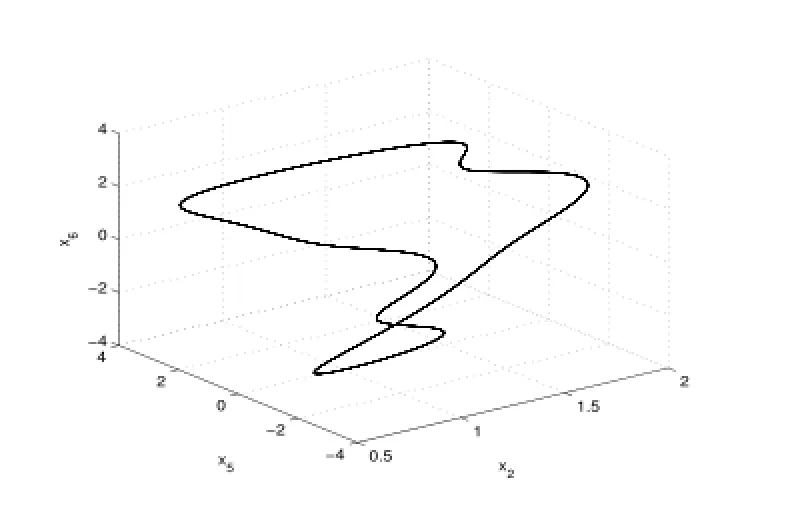
圖5：Re=30.2123

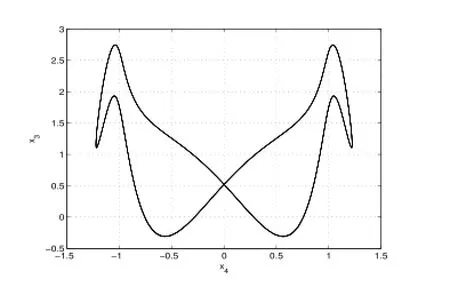
圖6：Re=30.2123

3）當Re=71.31時，平衡點p±處分叉出閉軌線開始不穩定，分叉處環面，如圖7，8.

4）當Re進一步增大時出現了滯后現象（各種吸引子共存），如圖9-13.當Re=248.23時系統發生混沌，出現奇怪吸引子，如下圖14-16分別給出了不同雷諾數時奇怪吸引子的大體狀態.通過數值計算表明系統在高雷諾數下一直是混沌狀態，這與文獻［1］的結論是一致的.

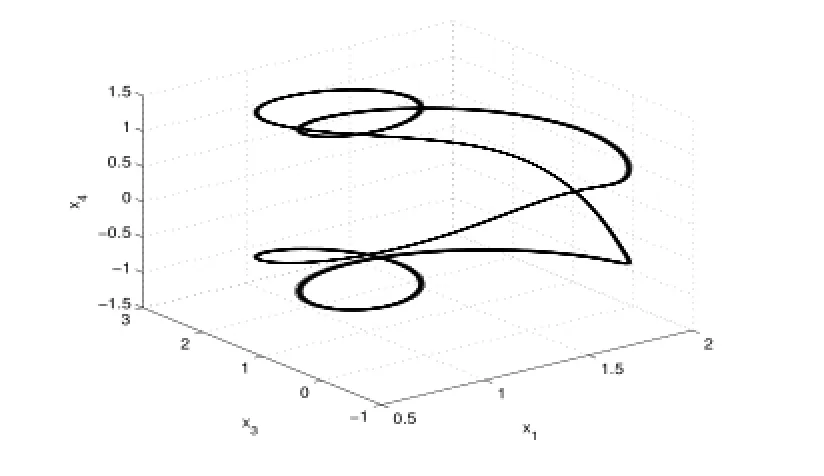
圖7：Re=71.4

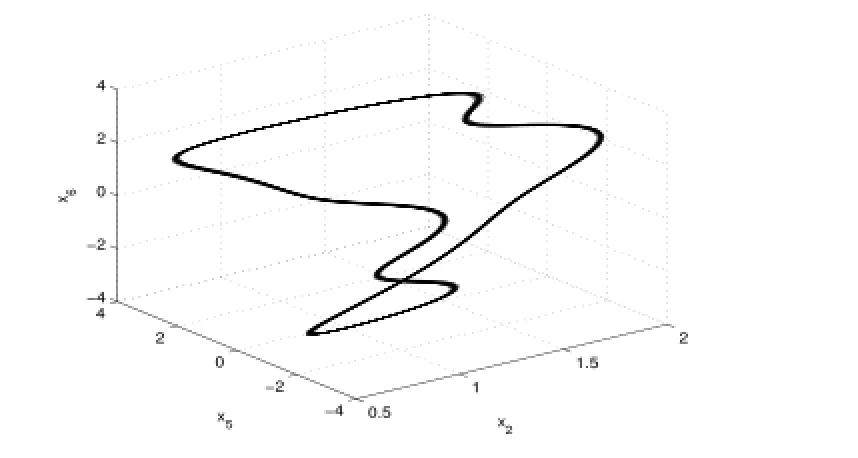
圖8：Re=72.0

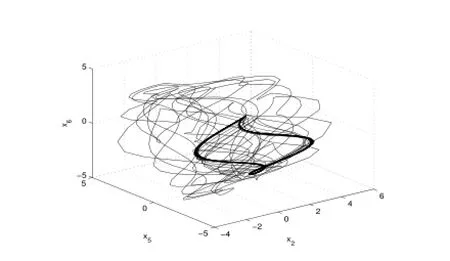
圖9：Re=72.5

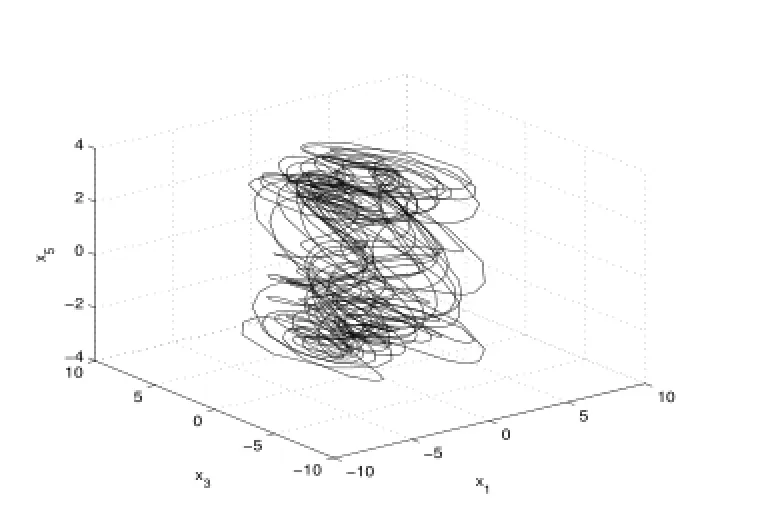
圖10：Re=73.8

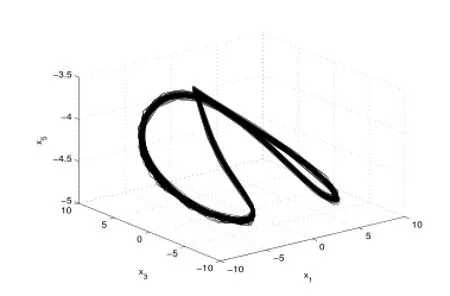
圖11：Re=202.4

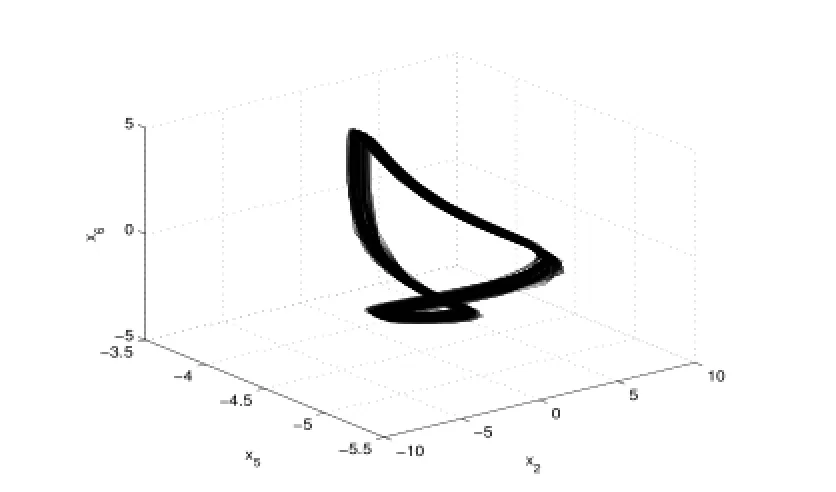
圖12：Re=220.54

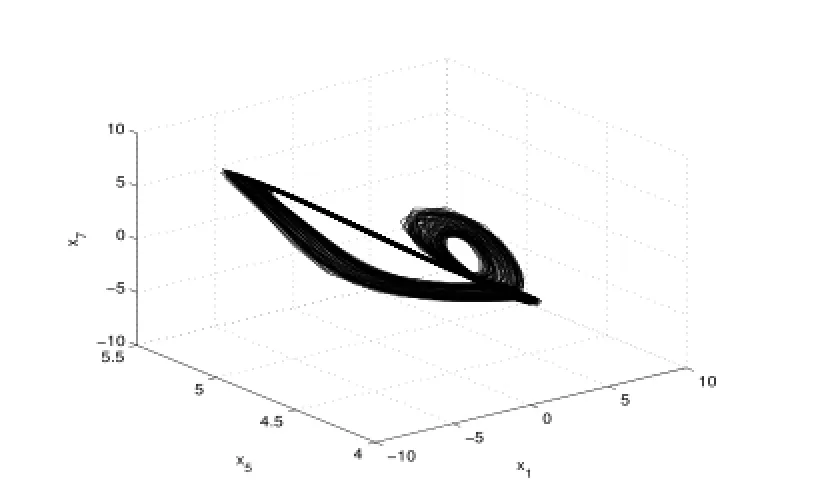
圖13：Re=230.24

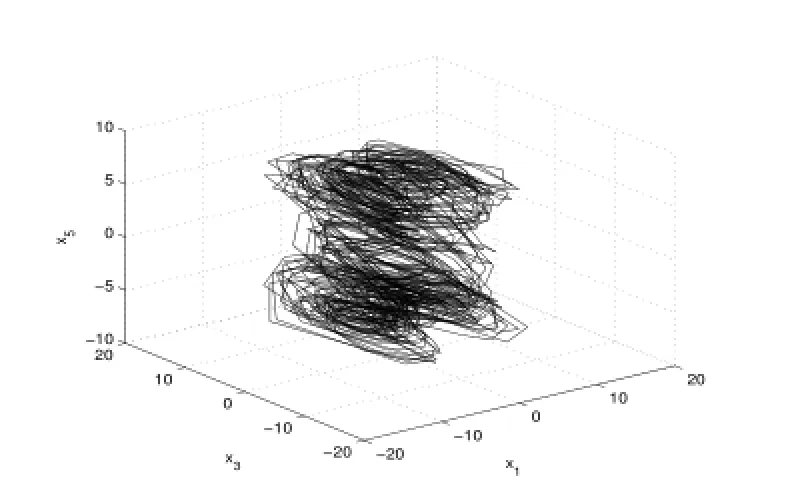
圖14：Re=248.23

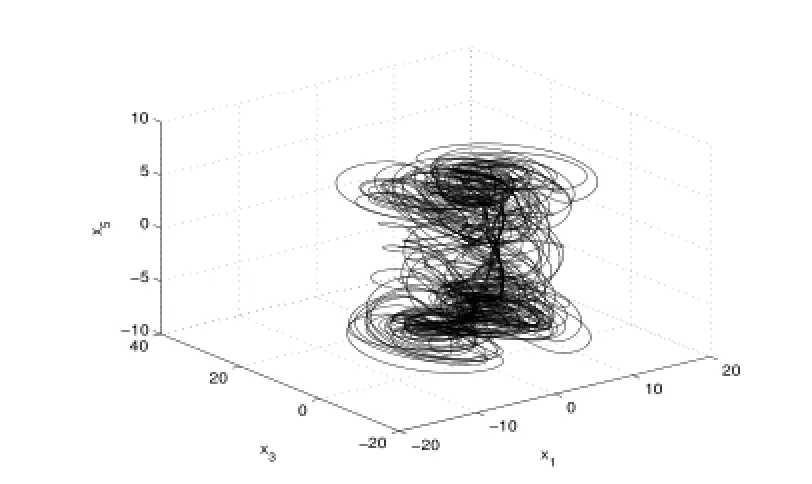
圖15：Re=249.44

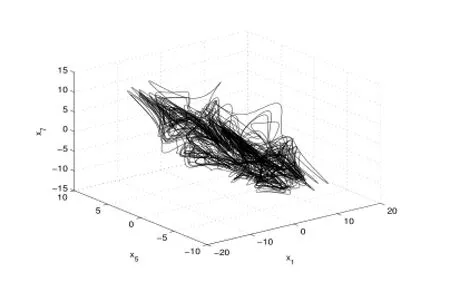
圖16：Re=255.64

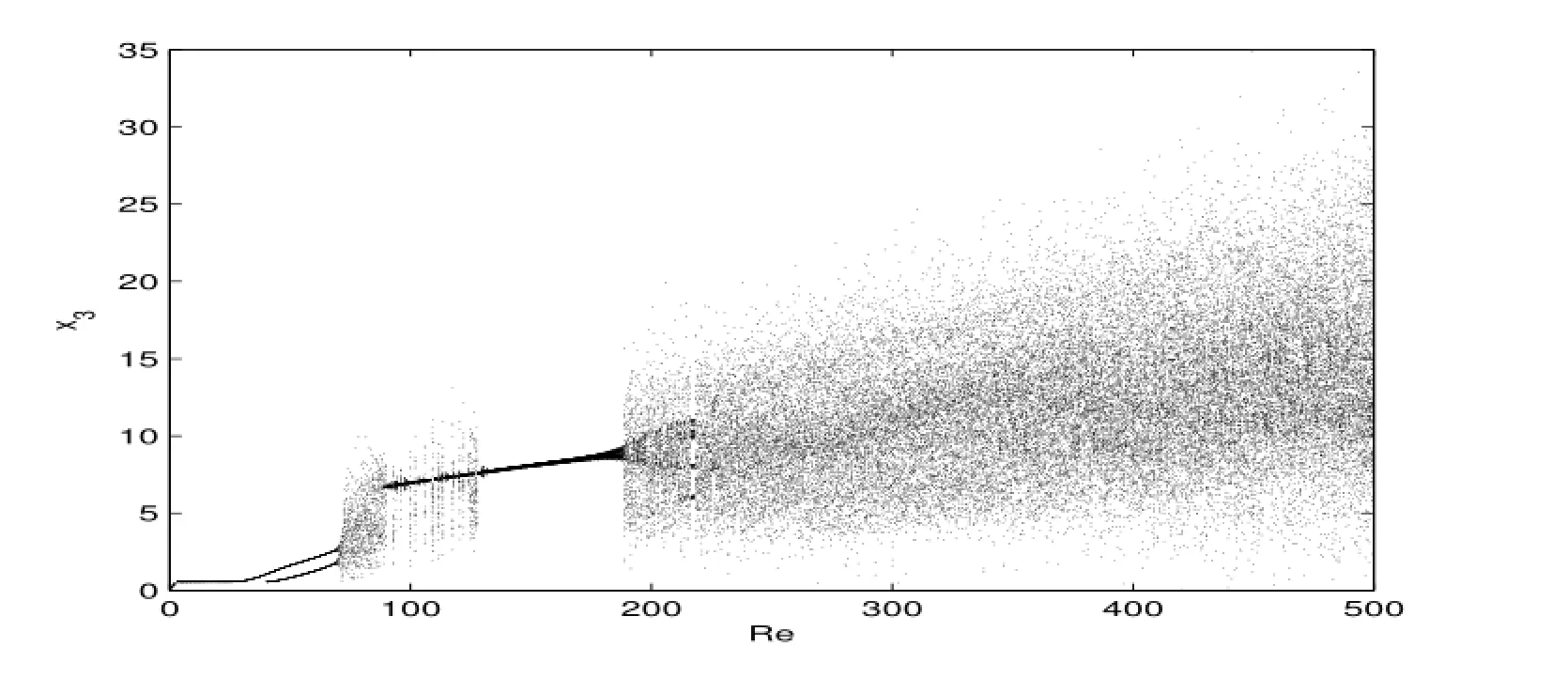
圖17：分叉圖

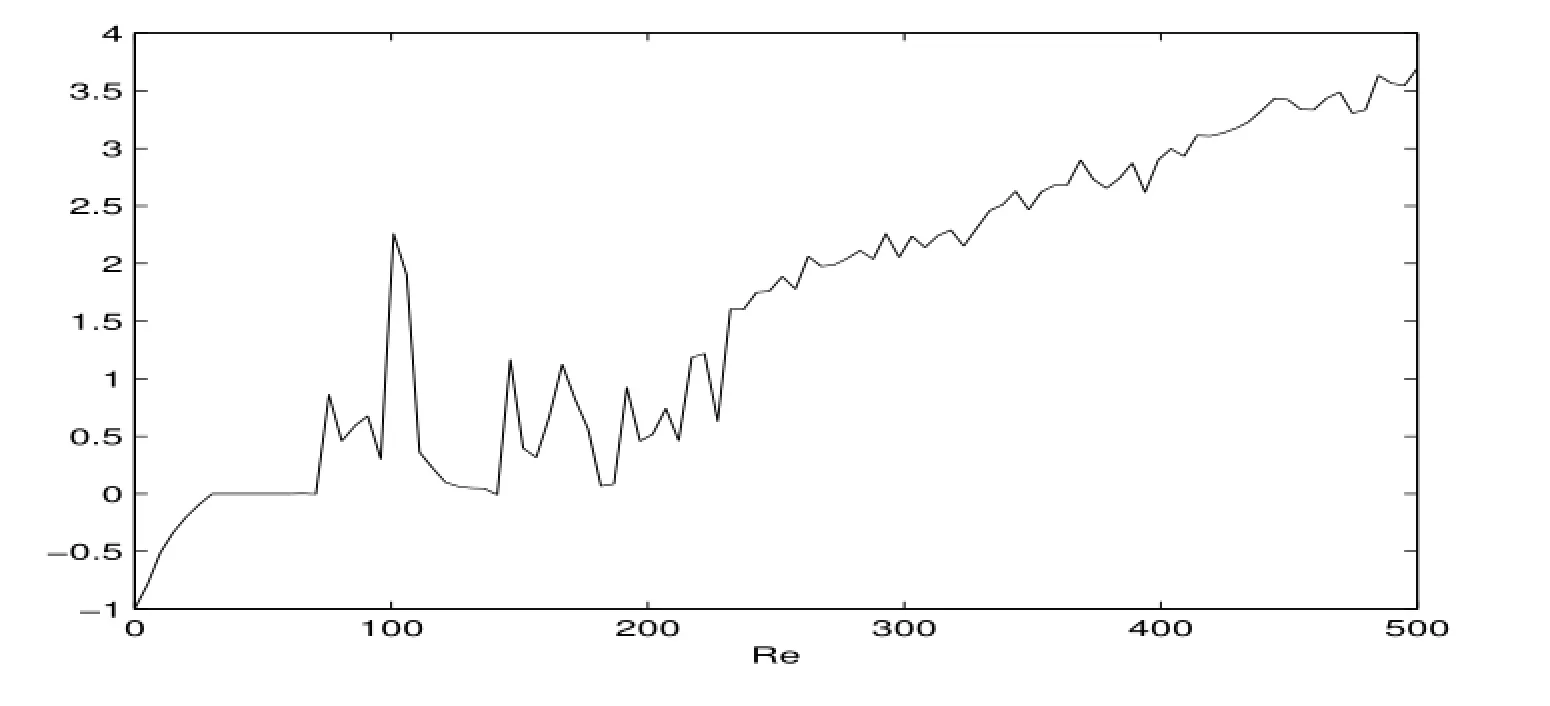
圖18：最大李雅普諾夫指數

5）圖17，18分別給出了系統分岔圖和最大李雅普諾夫指數，從分岔圖17表明：當Re＜71.31時，系統是穩定的，當Re=71.31時，系統開始不穩定，分叉處環面，之后系統出現滯后現象，當Re=248.23時系統發生混沌，出現奇怪吸引子，算到Re=1000系統始終是混沌狀態，在高雷諾數下系統處于湍流狀態，這一點也與lorenz系統有明顯的區別.圖18中給出的最大李雅普諾夫指數與分岔圖17是相符的.

6）圖19給出了系統的龐加萊截面（Re=252.41），圖20給出了系統的功率譜（Re= 255.24），它們均表明了系統的混沌運動特征.

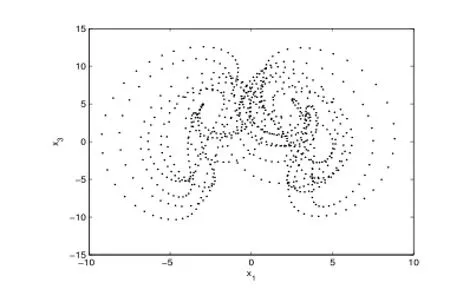
圖19：Re=252.41

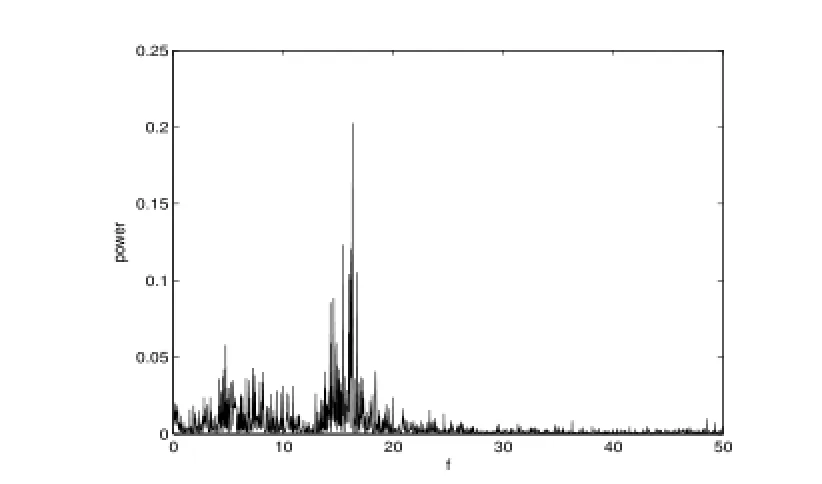
圖20：Re=255.24

6　結論

本文首先給出了七模類Lorenz方程組的推導過程，對此方程組線性化穩定性分析進行了簡單介紹.然后證明了此方程組全局吸引子的存在性，并對其全局穩定性進行了分析和討論，最后數值模擬了雷諾數變化時系統經由不變環面的失穩到達混沌的過程，運用分岔圖、最大李雅普諾夫指數、龐加萊截面和功率譜揭示了系統混沌行為的普適特征.

［1］Valter Franceschini，Claudio Tebaldi.A seven-modes truncation of the plane incompressible Navier-Stokes equations［J］.J.Stat.Phys.，1981，25（3）：397-417.

［2］Carlo Boldrighini，Valter Franceschini.A five-dimensional truncation of the plane incompressible Navier-Stokes equations［J］.Commun.Math.Phys.，1979，64：159-170.

［3］Franceschini V，Zanasi R.Three-dimensional Navier-Stokes equations trancated on a torus［J］.Nonl.，1992，4：189-209.

［4］Valter Franceschini，Claudio Tebaldi.Breaking and disappearance of tori［J］.Commun.Math.Phys.，1984，94：317-329.

［5］劉秉正，彭建華.非線性動力學［M］.北京：高等教育出版社，2004，406-415.

［6］謝應齊.非線性動力學數學方法［M］.北京：氣象出版社，2001，9-17.

［7］Franceschini V，Inglese G，Tebaldi C.A five-mode truncation of the Navier-Stokes equations on a three-dimensional torus［J］.Commun.Mech.Phys，1988，64：35-40.

［8］Chorin A，Marsden J，Smtle S.Mubalence seminar lecture notes in mathematics［M］.Berlin：Springer-Verlag，1988.

［9］Hilborn R C.Chaos and nonlinear dynamics［M］.Oxford：Oxford Univ.Press，1994．

［10］王賀元，姜悅嶺，平面不可壓縮Navier-Stokes方程新五模類Lorenz方程組的混沌行為［J］.數學雜志，2010，30（2）：269-272.

［11］高焱，磁流體動力學截斷方程組的動力學行為研究［J］.數學雜志，2013，33（4）：671-678.

［12］李開泰，馬逸塵.數理方程HILBERT空間方法（下）［M］.西安：西安交通大學出版社，1992.

THE DYNAMICAL BEHAVIOR AND THE NUMERICAL SIMULATION OF THE SEVEN-MODE TRUNCATION SYSTEM OF THE PLANE INCOMPRESSIBLE NAVIER-STOKES EQUATIONS

WANG He-yuan
（School of Sciences，Liaoning University of Technology，Jinzhou 121001，China）

The chaotic behavior of seven-mode Lorenz-like system for the plane incompressible Navier-Stokes equations is studied.By mode truncation，a seven-mode Lorenz equations is obtained.The existence of the attractor of the equations is proved，and the global stability of the equations is discussed.Based on numerical simulation results of bifurcation diagram，Lyapunov exponent spectrum，Poincare section and power spectrum of the system，general features of the system are revealed.The whole process，which shows a chaos behavior with the changing of Reynolds number，is simulated numerically.

Navier-Stokes equations；strange attractor；Liapunov function

MR（2010）主題分類號：65P20；65P40O175.14；O241.81

A

0255-7797（2016）05-1067-10

2014-07-13接收日期：2014-12-18

遼寧省教育廳科研基金（L2013248）；錦州市科學技術基金（13A1D32）資助；國家自然科學基金（11572146）.

王賀元（1963-），男，遼寧黑山，教授，主要研究方向：非線性系統的動力學行為及仿真.

2010 MR Subject Classification：65P20；65P40