與年齡相關的隨機分數階種群系統溫和解的存在性、唯一性

楊洪福，張啟敏

（北方民族大學數學與信息科學學院，寧夏銀川750021）

與年齡相關的隨機分數階種群系統溫和解的存在性、唯一性

楊洪福，張啟敏

（北方民族大學數學與信息科學學院，寧夏銀川750021）

本文研究了一類與年齡相關的隨機分數階種群動態系統.利用不動點定理、隨機分析和算子半群理論，討論了與年齡相關的隨機分數階種群系統溫和解的存在性、唯一性.本文是隨機整數階種群系統的推廣.

存在性；唯一性；隨機分數階種群系統；溫和解

1　引言

近年來，隨機分數階微分方程引起了國內外學者的關注，并被廣泛的應用在物理、生物、工程、金融等領域［1［6，7］.

另一方面，分數階微分方程與分形密切相關，而分形富含于生物系統中.研究表明，在傳統的整數階微分方程不能建模的現象中，分數階微分方程為此提供了可能性.這里，特別強調的是，分數階與整數階模型最大區別在于分數階模型擁有記憶，而死亡率有長程相似性，它的主要特征恰恰包含了記憶.因此，本文首次嘗試建立與年齡相關的隨機分數階動力學模型.另外，已經證實由分數階微分方程建立的某些生物學模型比整數階更有優勢［8，9］.

現在將分數階引入與年齡相關的隨機種群模型［10］.新系統可描述為如下分數階非線性系統：

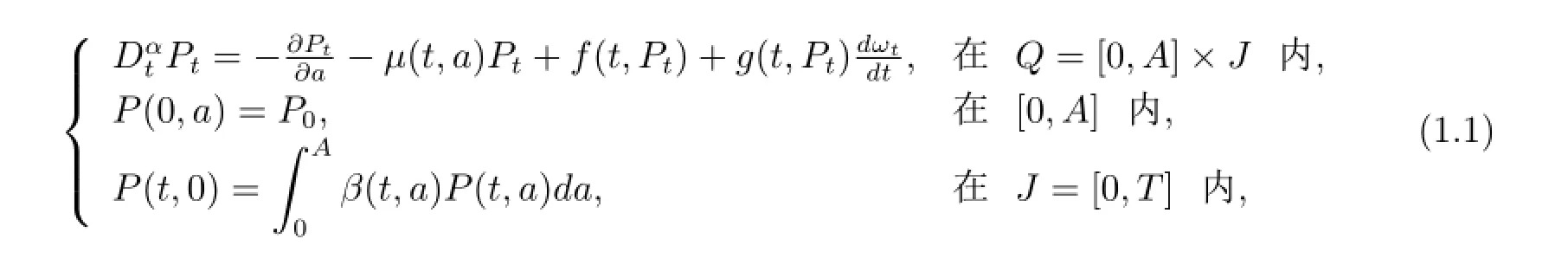
其中0＜α＜1，a∈［0，A］表示年齡，t∈［0，T］表示時間，0＜T＜∞，Pt：=P（t，a）、β（t，a）和μ（t，a）分別表示時刻t年齡為a的種群密度、生育率和死亡率.f（t，P）為外部環境對種群系統的影響，如遷移、地震等突發性災害對種群引起的影響,為隨機外界環境對系統的擾動.

在α=1的情況下，方程（1.1）成為經典的與年齡相關的隨機種群模型，該模型通過隨機分析理論和數值方法已被廣泛研究.例如張啟敏等［10］研究了與年齡相關的隨機種群方程解的存在性，唯一性和指數穩定性.李榮華等［11］考慮了帶Markovian跳的與年齡相關的隨機種群方程數值解的收斂性.馬維軍和張啟敏等［12，13］討論了與年齡相關的隨機種群方程帶分數布朗運動的數值解和Markovian跳的漸近穩定性.楊洪福等在文獻［14］中介紹了與年齡相關的隨機兩種群方程在POD基下的數值解.

本文首次將分數階引入與年齡相關的隨機種群動力學模型，討論在滿足一定的假設條件下證明了溫和解的存在性、唯一性，得到的結論是文獻［10］的推廣.

2　預備知識

令

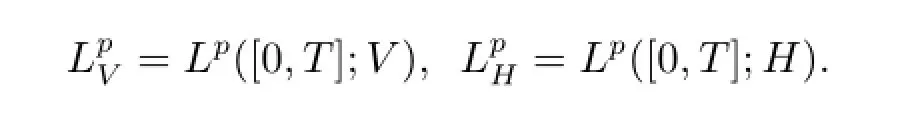
下面，首先給出兩個相關的基本定義.

定義2.1［4］函數f的α分數階積分定義為

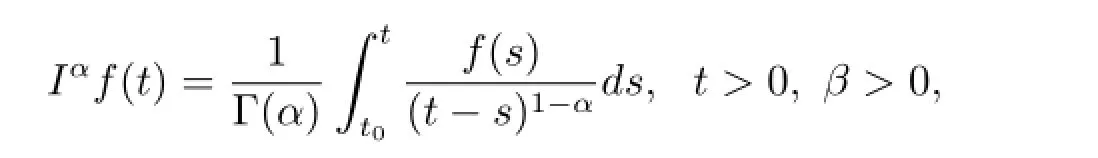
其中t≥t0且α＞0，Γ（·）為Gamma函數.

定義2.2［15，16］函數f的α階Caputo分數階微分定義為

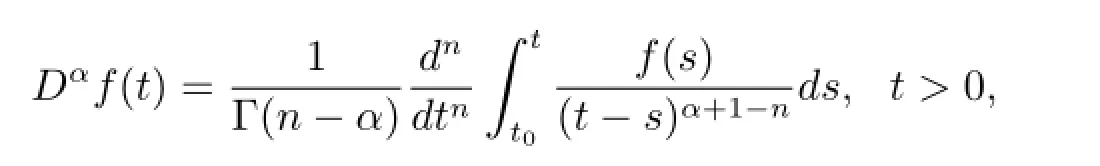
其中t≥t0，n是一個正整數滿足n-1＜α＜n.特殊地，當0＜α＜1時，

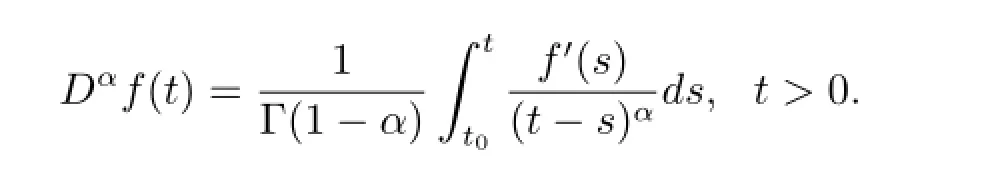
把與年齡相關的隨機分數階種群方程（1.1）寫成如下形式的積分方程［16］

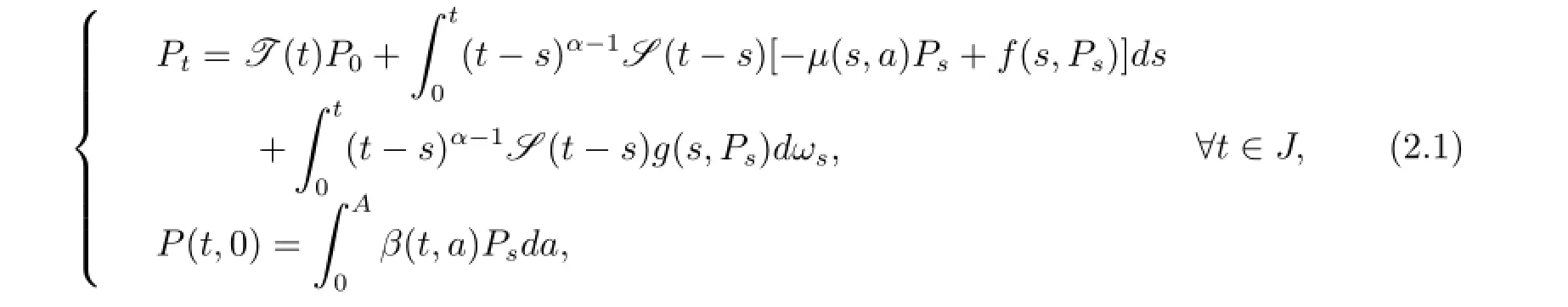
其中

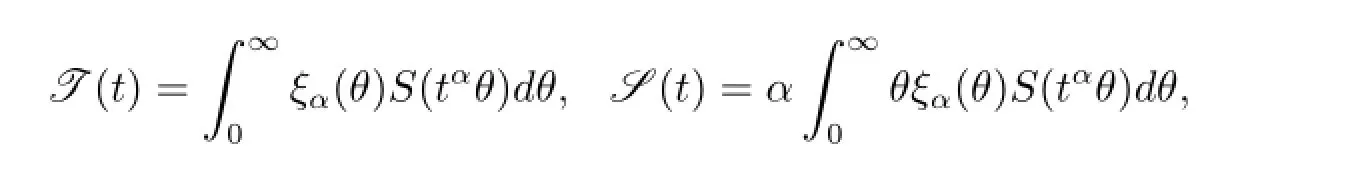
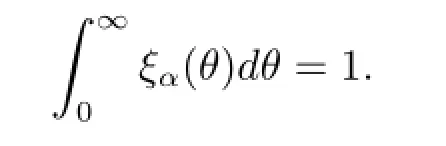
定義2.3［17］如果一個Ft-循序可測的隨機變量｛P（t，a）｝t∈J是方程（1.1）的一個溫和解，則｛P（t，a）｝t∈J滿足相應的積分方程（2.1）.

引理2.4［18］如果算子和是強連續的，則對每個Pt∈H，當t1→t2，有

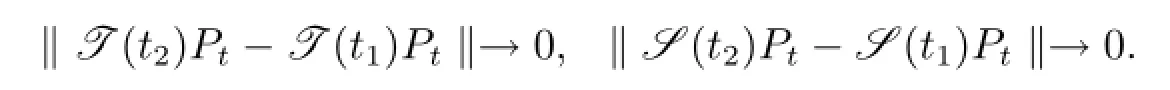
為了證明本文的主要結論，給出以下假設條件：（i）μ（t，a）非負可測，并且

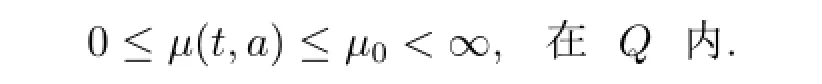
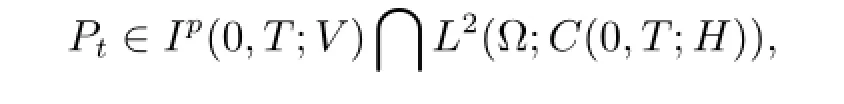
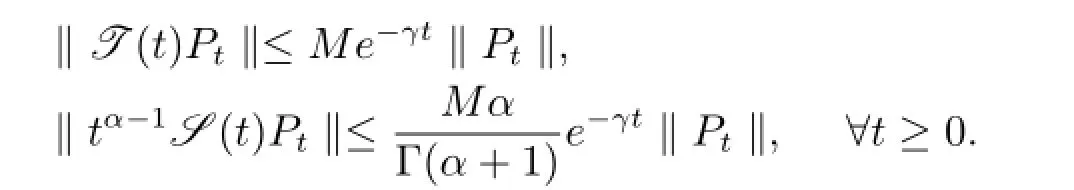
（a.2）?N＞0，使得

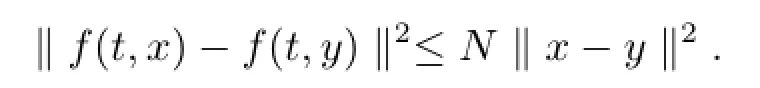
（b.1）g（t，0）=0；

（b.2）?L＞0，使得

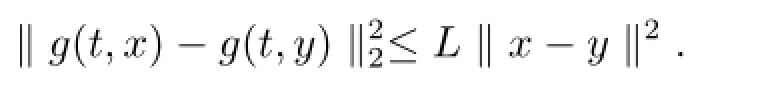
3　溫和解的存在性、唯一性

在本節中，利用第二部分給出的定義和引理，證明與年齡相關的隨機分數階種群方程（1.1）的溫和解的存在性、唯一性.定義算子Ψ：H→H，滿足如下方程為了證明文章的主要結論，先證明如下引理.

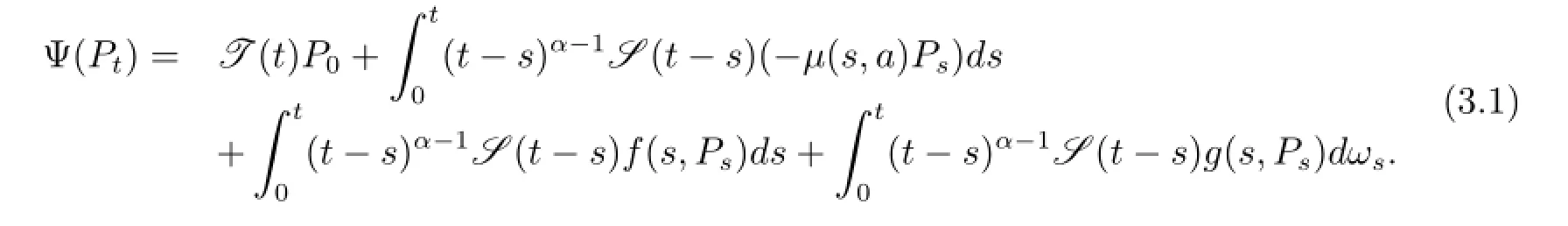
引理3.1對任意的Pt∈H，ΨPt在［0，T］上是L2-連續的.

證令0＜t1＜t2＜T.對于方程（3.1）的任意固定點Pt∈H，有

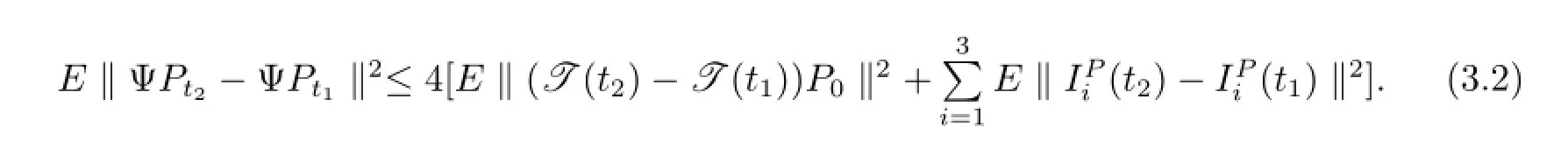
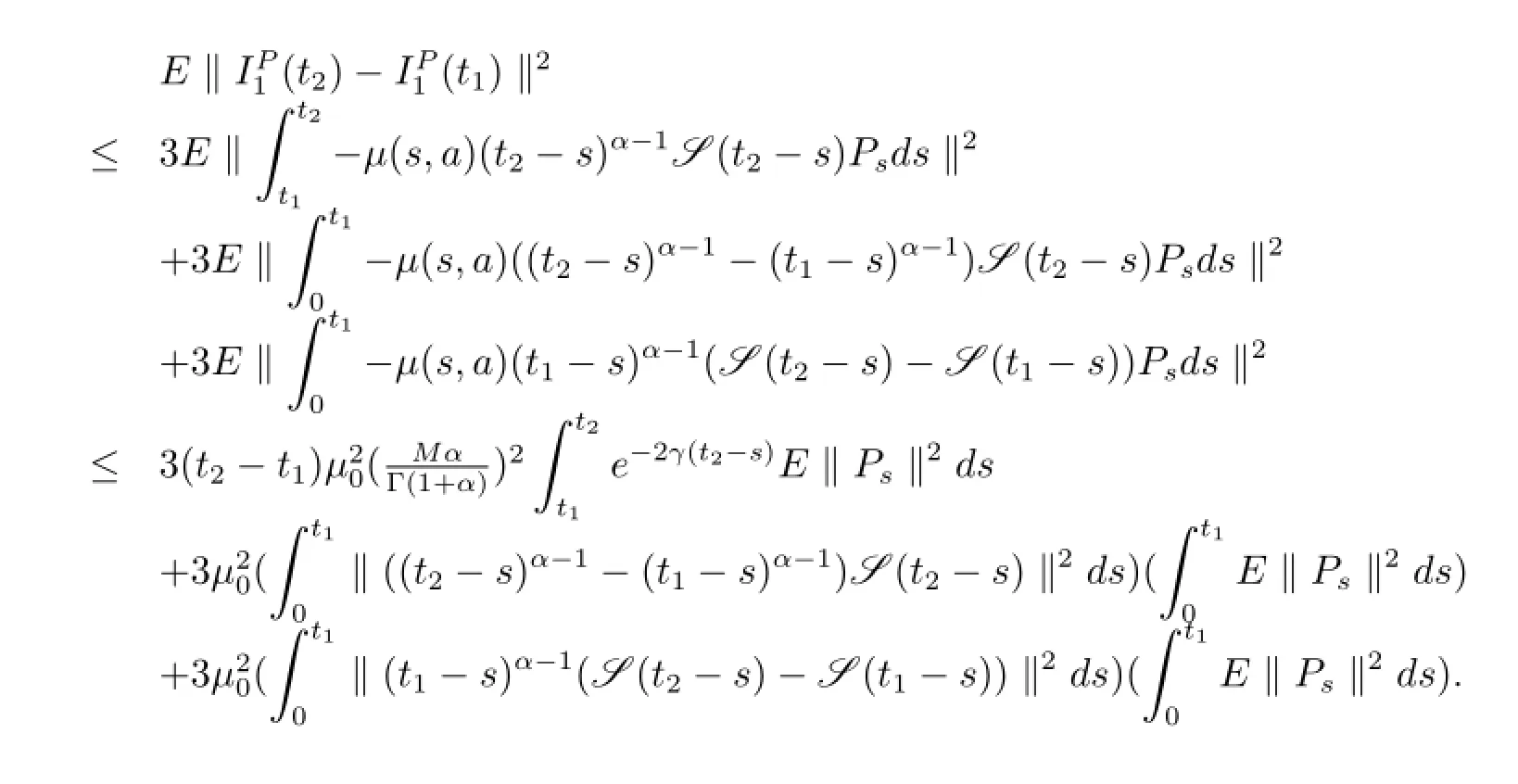
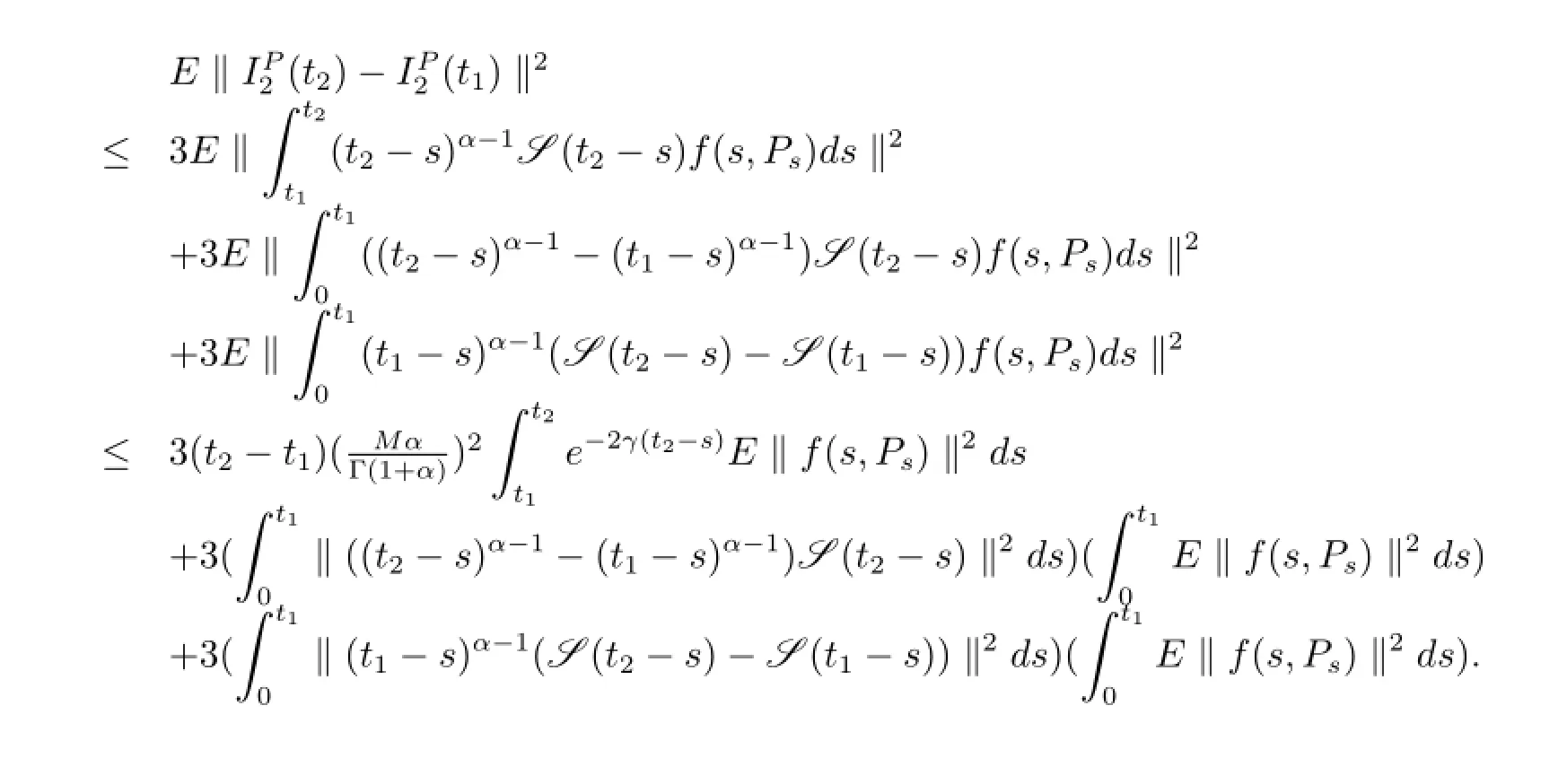
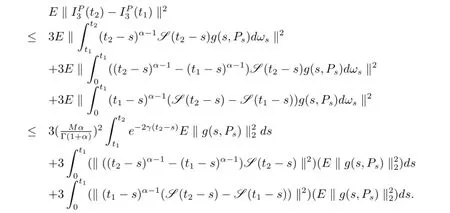
類似的可以證明在［0，T）上ΨPt是左連續.因此引理得證.

定理3.2如果條件（i）-（iii）是成立的，并且滿足下面的不等式，則方程（1.1）存在唯一的溫和解Pt∈H.

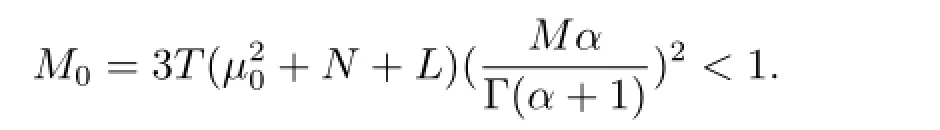
證應用壓縮映射原理證明算子Ψ存在一個不動點.首先，要證Ψ（H）?H.令Pt∈H，由（3.1）式，可得

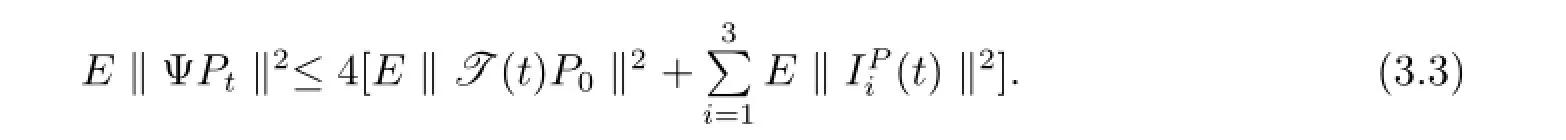
現在估計方程（3.3）右邊的項.第一項，由條件（ii）可得

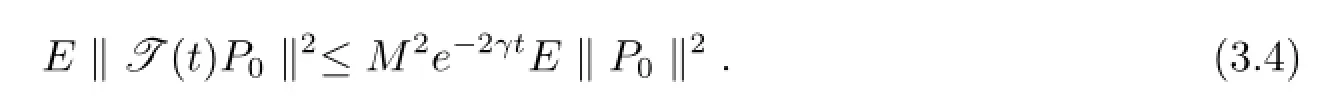
第二項應用Holder不等式和假設條件（i）-（iii）有

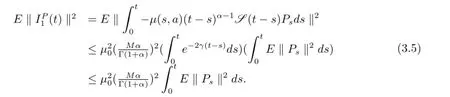
進一步又可以得到

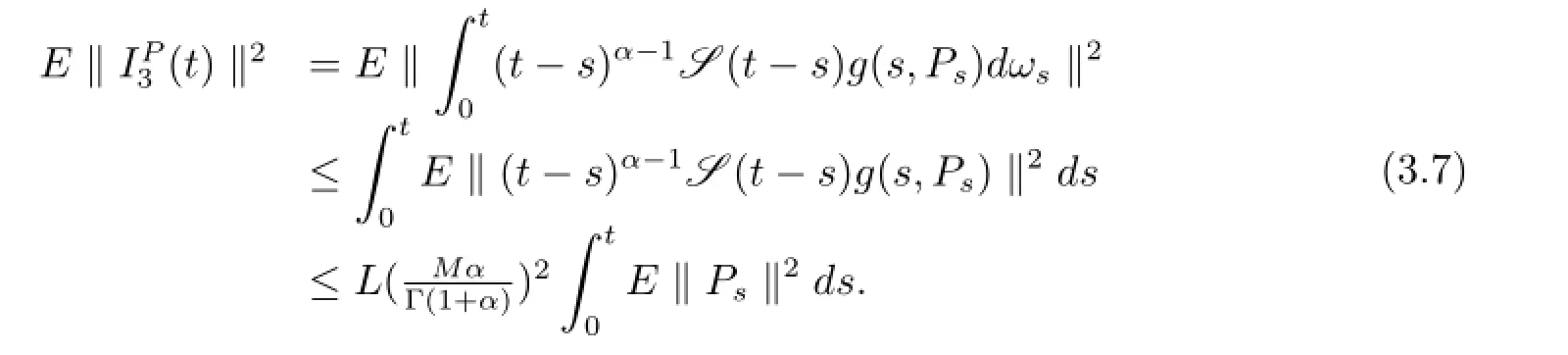
所以從（3.4）式到（3.7）式可以得到E‖ΨPt‖2＜∞.由引理3.1知ΨPt∈H.因此算子Ψ是從H到H的自映射.接下來，將證明Ψ是H上的連續映射.事實上，對任意的P1t，P2t∈H，由方程（3.1）和等距公式，可得

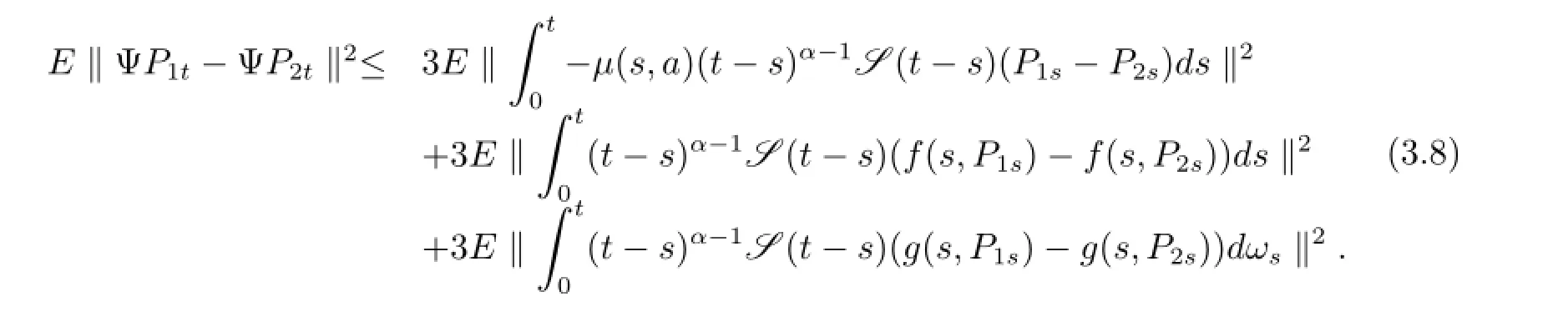
現在估計方程（3.8）右邊的項.第一項由Holder不等式和假設條件（i）-（iii），有

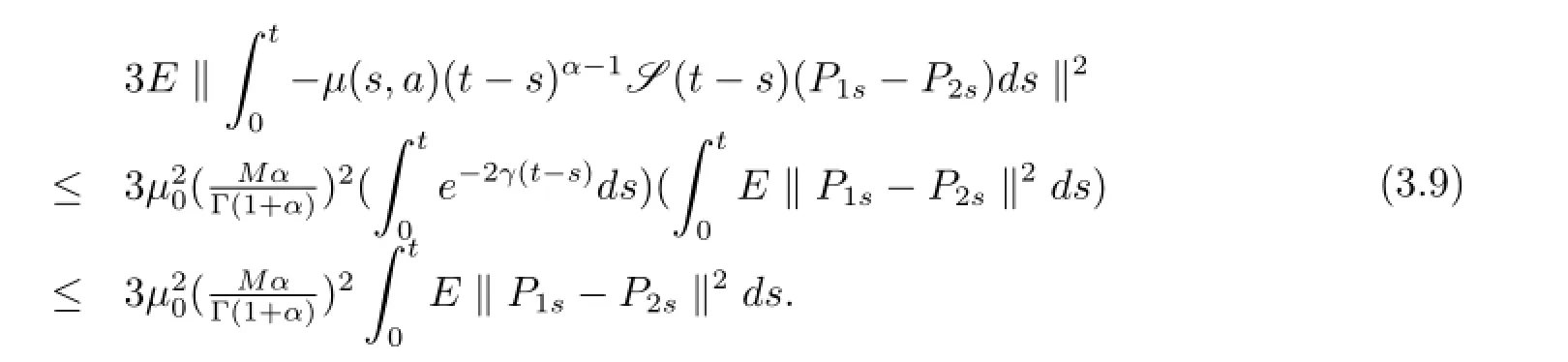
類似的，第二項為

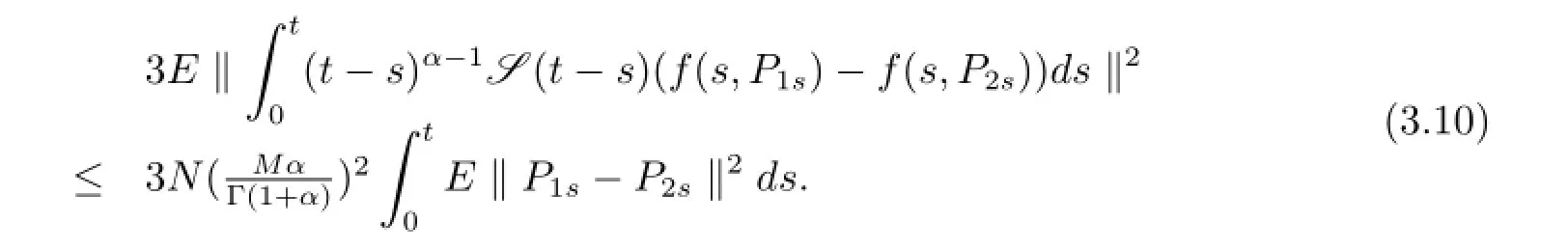
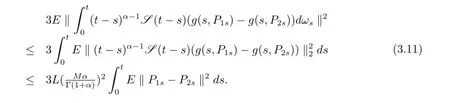
因此?t∈J由方程（3.9）-（3.11）可以得到

即

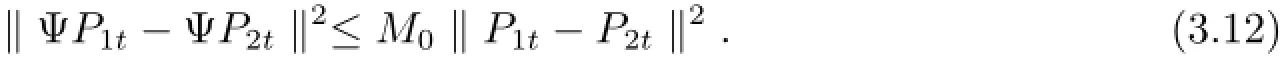
從方程（3.12）可以得出Ψ是連續映射.由Banach壓縮映射原理，在H上存在唯一不動點Pt，使得ΨPt=Pt.因此可以得到

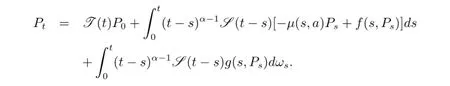
即Pt∈H是方程（1.1）的溫和解.定理得證.

4　結論

本文用分數階導數代替古典的隨機種群系統中關于時間的整數階導數，得到了一類隨機分數階種群模型，該模型較傳統的隨機種群系統能更好地刻畫現實中的種群問題，尤其對具有遺傳性的種群現象.在引入分數階概念的基礎上，利用不動點定理、隨機分析和算子半群理論，討論了隨機分數階種群系統溫和解的存在性、唯一性.所得到的結論為種群未來的研究提供了一定的理論依據.

［1］He J H.Nonlinear oscillation with fractional derivative and its applications［J］.Intern.Confer.Vibrating Engin.，1998，288-291.

［2］Cui Z J，Yang Z D.Application of homotopy perturbation method to nonlinear fractional population dynamics models［J］.Intern.J.Appl.Math.Comput.，2012，4（4）：403-412.

［3］Xu H.Analytical approximations for a population growth model with fractional order［J］.Commun. Nonl.Sci.Numer.Simulat.，2009，14：1978-1983.

［4］Shu X B，Lai Y，Chen Y.The existence of mild solutions for impulsive fractional partial differential equations［J］.Nonl.Anal.TMA，2011，74：2003-2011.

［5］Liu Kewei，Jiang Wei.Finite time stability of fractional order neutral differential equations［J］.J. Math.，2014，1：43-50.

［6］Wang Y W，Guan Z H，Xiao J W.Impulsive control for synchronization of a class of continuous systems［J］.Chaos，2004，14（1）：199-203.

［7］胡建兵，韓焱，趙靈冬.分數階系統的一種穩定性判定定理及在分數階統一混沌系統同步中的應用［J］.物理學報，2009，58（7）：4402-4406.

［8］Cole K S.Electric conductance of biological systems［J］.Proc.Cold Spring Harbor Symp.Quant. Biol.，New York：Cold Spring Harbor，1993：107-116.

［9］Anastasio T J.The fractional-order dynamics of bainstem vestibulo-oculomotor neurons［J］.Biol. Cyber.，1994，72：69-79.

［10］Zhang Q M，Liu W A，Nie Z K.Existence，uniqueness and exponential stability for stochastic age-dependent population［J］.Appl.Math.Comput.，2004，154：183-201.

［11］Li R L，Leung P，Pang W.Convergence of numerical solutions to stochastic age-dependent population equations with Markovian switching［J］.J.Comput.Appl.Math.，2009，233：1046-1055.

［12］Ma W J，Zhang Q M，Wang Z P.Asymptotic stability of stochastic age-dependent population equations with Markovian switching［J］.Appl.Math.Comput.，2014，227：309-319.

［13］Ma W J，Zhang Q M，Han C Z.Numerical analysis for stochastic age-dependent population equations with fractional Brownian motion［J］.Commun.Nonl.Sci.Numer.Simul.，2012，17：1884-1893.

［14］Yang H F，Zhang Q M，Feng J T.Numerical simulations based on POD for stochastic age-dependent system of two species［J］.Differ.Equ.Dyn.Syst.，2015，23（4）：433-451.

［15］Jiang H P，Jiang W.The existence of a positive solution for nonlinear fractional functional differential equations［J］.J.Math.，2011，3（31）：440-446.

［16］Chen L P，Chai Y，Wu R C，Ma T D，Zhai H Z.Dynamic analysis of a class of fractional-order neural networks with delay［J］.Neurocomputing，2013，11：190-194.

［17］Sakthivel R，Revathi P，Anthoni S M.Existence of pseudo almost automorphic mild solutions to stochastic fractional differential equations［J］.Nonl.Anal.，2012，75：3339-3347.

［18］Sakthivel R，Suganya S，Anthoni S M.Approximate controllability of fractional stochastic evolution equations［J］.Comp.Math.Appl.，2012，63：660-668.

EXISTENCE，UNIQUENESS FOR STOCHASTIC
FRACTIONAL-ORDER AGE-DEPENDENT POPULATION

YANG Hong-fu，ZHANG Qi-min
（School of Mathematics and Information Science，Beifang University for Nationalities，Yinchuan 750021，China）

In this paper，we study a class of stochastic fractional-order age-dependent population dynamic system.By using fixed point theorem，stochastic analysis and semigroup of operators theory，the main conclusion of the existence and uniqueness of mild solution to stochastic fractional-order age-dependent population equations are obtained.This paper is a generalization of the stochastic integer order population system.

existence；uniqueness；stochastic fractional-order population system；mild solution

MR（2010）主題分類號：26A36；35R11；34D20；60H15O211.63

A

0255-7797（2016）05-1083-08

2014-10-30接收日期：2015-06-02

國家自然科學基金（11461053；11261043）；寧夏自然科學基金（N215104）.

楊洪福（1986-），男，黑龍江大興安嶺，碩士，主要研究方向：應用概率統計與非線性動力系統.通訊作者：張啟敏.

2010 MR Subject Classification：26A36；35R11；34D20；60H15