改進FAHP在高職院校實訓課程評價中的應用

王保敏，黃　珊

（1.安徽商貿職業技術學院 電子信息工程系，蕪湖241002；2.安徽機電職業技術學院 經貿管理系，蕪湖241002）

改進FAHP在高職院校實訓課程評價中的應用

王保敏1，黃珊2

（1.安徽商貿職業技術學院 電子信息工程系，蕪湖241002；2.安徽機電職業技術學院 經貿管理系，蕪湖241002）

將改進冪法引入模糊層次分析，提出了改進的模糊層次分析法。對每次迭代的中間結果做規范化處理，優化了模糊層次分析法的計算過程，減少了判斷矩陣權重向量的計算步驟，避免了一致性檢驗的繁瑣過程，提高了計算效率。以高職院校一門實訓類課為研究對象，構建了相應的指標評價體系，并通過改進的模糊層次分析法評價了教學效果，得到了比較理想的計算結果。

模糊層次分析法（FAHP）；課程評價；判斷矩陣；改進冪法

層次分析法（AHP）是一種定性分析與定量計算相結合的分析方法，也是解決評價對象屬性多樣化和結構復雜化問題的一種方法。在對備選方案優選過程中，人們通過建立多要素和多層次的評價體系，將各評價因素分為目標層、中間層（準則層）和方案層［1］，并通過4個步驟［2］求解。求解的4個步驟分別是：建立遞階層次結構，構建判斷矩陣并進行一致性檢驗，計算評價因素的相對權重，合成總權重后對備選方案進行排序并確定目標方案。層次分析法簡潔實用，所需數據少，已在計劃制定、方案求解等方面得到了廣泛的應用［3］。在本文中，我們提出了改進的模糊層次分析法，優化了評價因素的計算步驟，并將該方法用于評價高職院校實訓課程的教學效果，得到了比較滿意的評價結果。

1　改進的模糊層次分析法

1.1層次分析法的不足

在求解各要素的相對權重時，常用的層次分析法包括求和法、方根法等，但這些方法需要做判斷矩陣的一致性檢驗，當要素較多（矩陣的階數較大）時，精確求解的工作量往往很大，還需要做多次調整與檢驗。隨著應用領域的擴大，迫切需要克服層次分析法的這些缺點。因此，模糊層次分析法［4］應運而生，并被不斷優化，其中的最優傳遞矩陣法能消除專家評判的不一致性［5］，提高了決策的可靠性和科學性。

1.2計算方法的改進

模糊層次分析法的關鍵步驟是確定各因素的相對權重，計算權重實質上就是計算判斷矩陣的最大特征值λ1對應的特征向量X1。由于誤差的敏感性和高次方程的難解性，用線性代數方法求特征向量存在較大局限性。因此，我們通過乘冪法的不斷迭代的思想求出特征向量的近似最優解。

定理1：設矩陣A有n個線性無關的特征向量，對應的n個特征值滿足，則對任何非零初始向量所構成的迭代序列，有，其中和分別表示和的第j個分量。

X1，X2，…，Xn的線性組合表示，即，其中

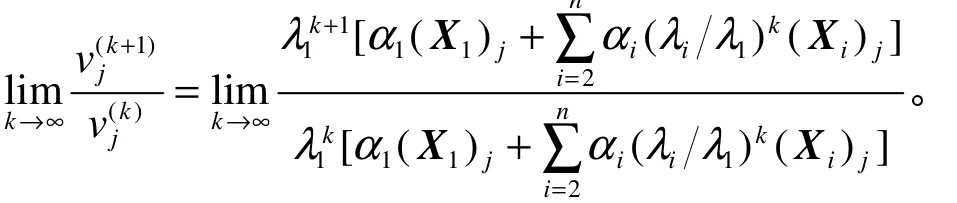
特別地，若λ1是m重根，即且，此時，有

1.3求解步驟

步驟1.建立評價系統的遞階層次結構。

步驟2.構造初始判斷矩陣，并將其轉換為模糊一致矩陣。

步驟3.利用改進冪法求模糊一致矩陣的最大特征值和對應的特征向量，便可得到比較要素相對于上一層因素的相對權重。其中，改進冪法的迭代過程如下：先取初始值，再取，最后計算

步驟4.計算總權重，對備選方案進行排序，得出最優方案。

2　高職院校實訓課程的評價指標體系

高職院校實訓課程的教學注重學生技能的培養，因此，教學效果取決于學生、教師、教法和軟硬件條件等因素。鑒于此，我們制定了高職院校實訓課程的評價指標體系（圖1）。

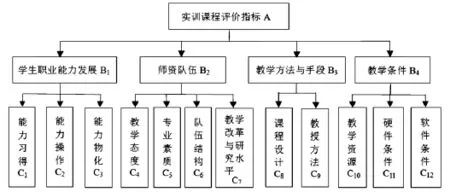
圖1　實訓課程評價指標體系

從圖1可以看出，實訓課程的一級評價指標包括“學生職業能力發展”“師資隊伍”“教學方法與手段”和“教學條件”4個因素。每個因素可根據需要做進一步劃分。例如，“學生職業能力發展”可以劃分為“能力習得”“能力操作”和“能力物化”3個因素。其中，“能力物化”是指學生學習實訓課程后以物質形式表現出的能力水平，包括職業技能認證、技能大賽和成品結果等內容［6］。

3　應用實例

3.1建立判斷矩陣

我們根據文獻［7］的第二類標度（互補性標度）中標度構建模糊互補判斷矩陣，兩個因素之間的重要性程度如表1所示。

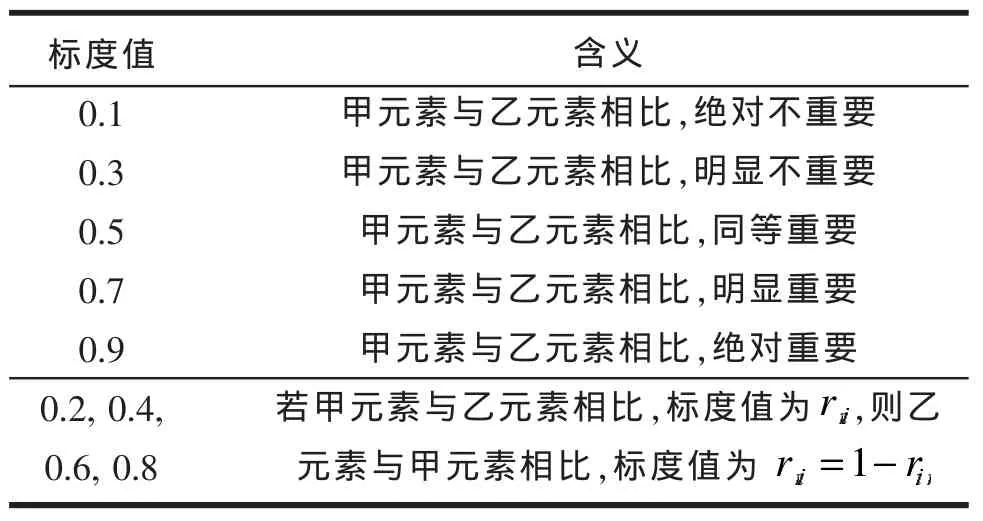
表1　0.1～0.9標度的重要性程度

記矩陣X?Y 表示下層Y 中元素對上層X 中某元素的優先判斷矩陣，其中的數值可以通過專家打分得出。根據這一思想，我們構建了5個初始模糊互補矩陣，分別記為和。其中數據見表2到表6。

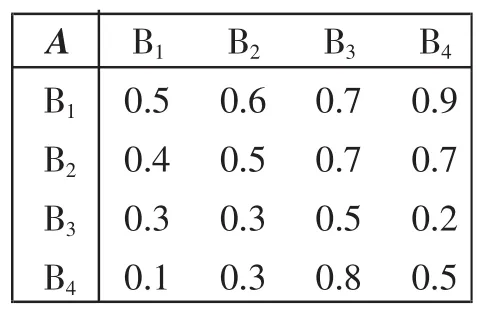
表2　A-B模糊互補矩陣

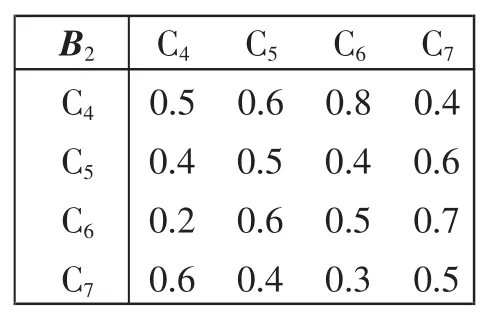
表3　B2-C模糊互補矩陣

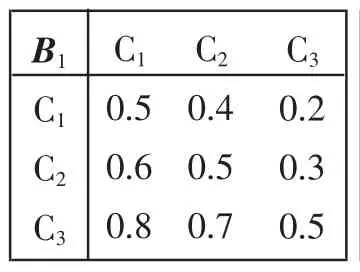
表4　B1-C模糊互補矩陣

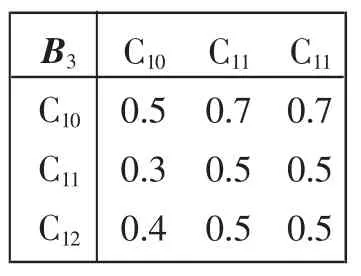
表5　B3-C模糊互補矩陣

表6　B4-C模糊互補矩陣

3.2計算相對權重

以B2-C矩陣為例，利用文獻［7］中的公式將該矩陣（表3）轉換成模糊一致矩陣，記為R1，即

從表7和表8可以看出，經過規范化處理后，每一次迭代結果的分量均控制在-1～1之間，運算過程中沒有發生溢出現象，這保證了最終解的計算精度。這兩種計算結果顯示：從k=5開始，最大特征值的結果趨于穩定，這與矩陣的階數較小有關；當判斷因素較多、矩陣階數較大時，用改進冪法計算能較快求得較高精度的解。

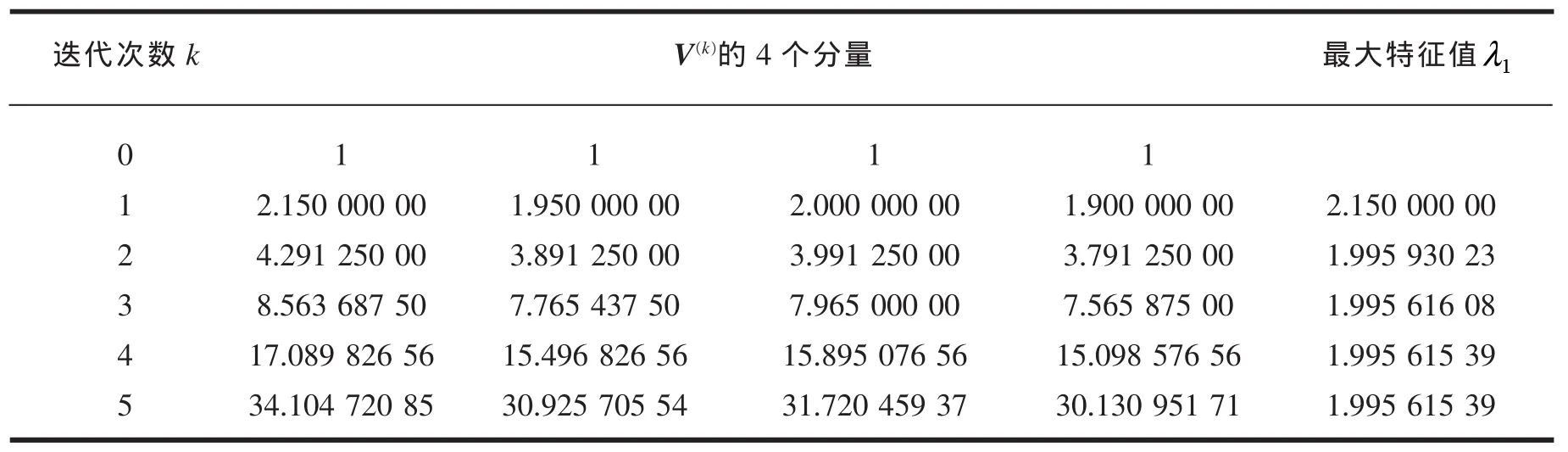
表7　乘冪法的迭代過程及計算結果

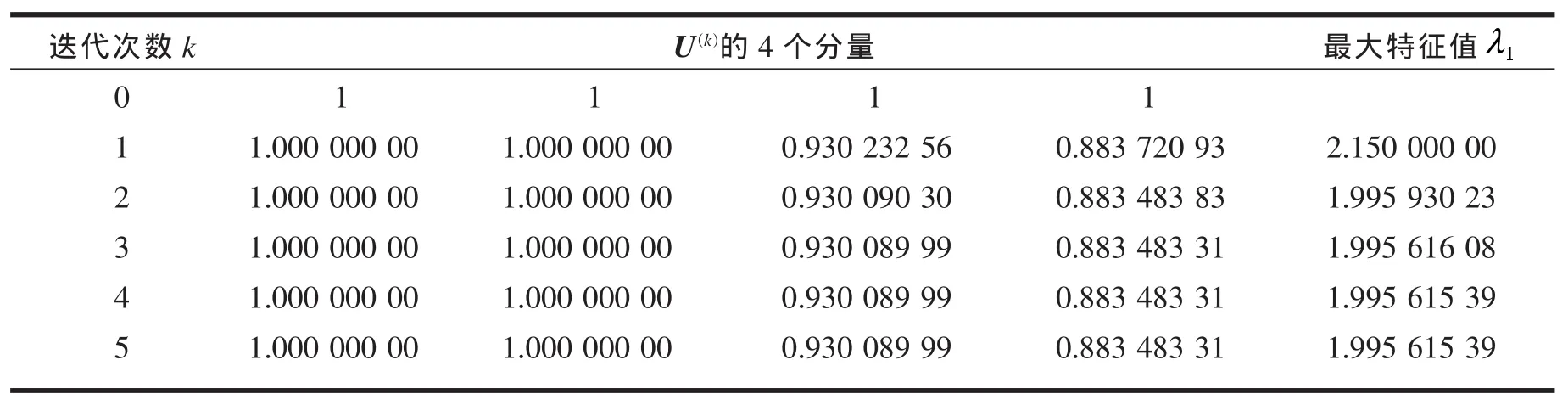
表8　改進冪法的迭代過程及計算結果

從表8可以看出，求得的結果是最大特征值λ1=1.99561539，對應的特征向量為（1.000 000 00 0.906 786 65，0.930 089 99，0.883 483 31）T，對該特征向量做歸一化處理，并保留6位小數，即可得準則層在目標層下的相對權重向量WA=(0.268 791, 0.243736, 0.250 000,0.237 473)T。同理可得其余各準則層的相對權重，匯總后的結果見表9。

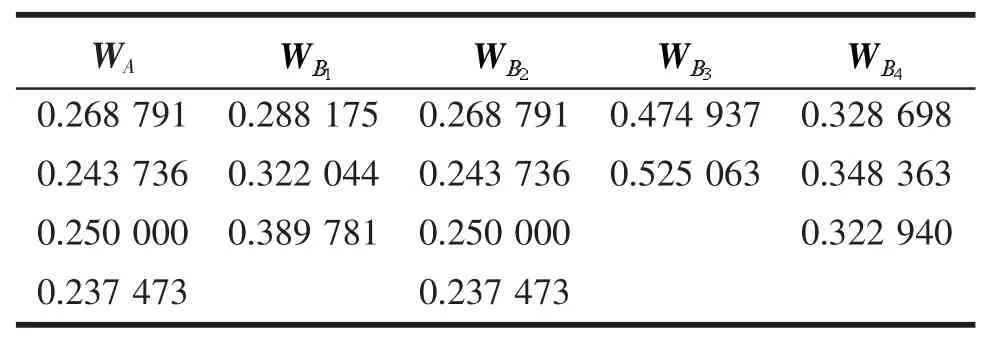
表9　準則層的相對權重

3.3模糊綜合評判的結果

針對12（C1—C12）個評價因素，我們請10個評價者按照優、良、中和差4個等級分別進行評價。比如，針對因素C1，有5名評價者認為其等級為“優”，有3名評價者認為其等級為“良”，有2名評價者認為其等級為“中”。評價完成后，將所有因素的評價結果進行歸一化處理，結果見表10。，

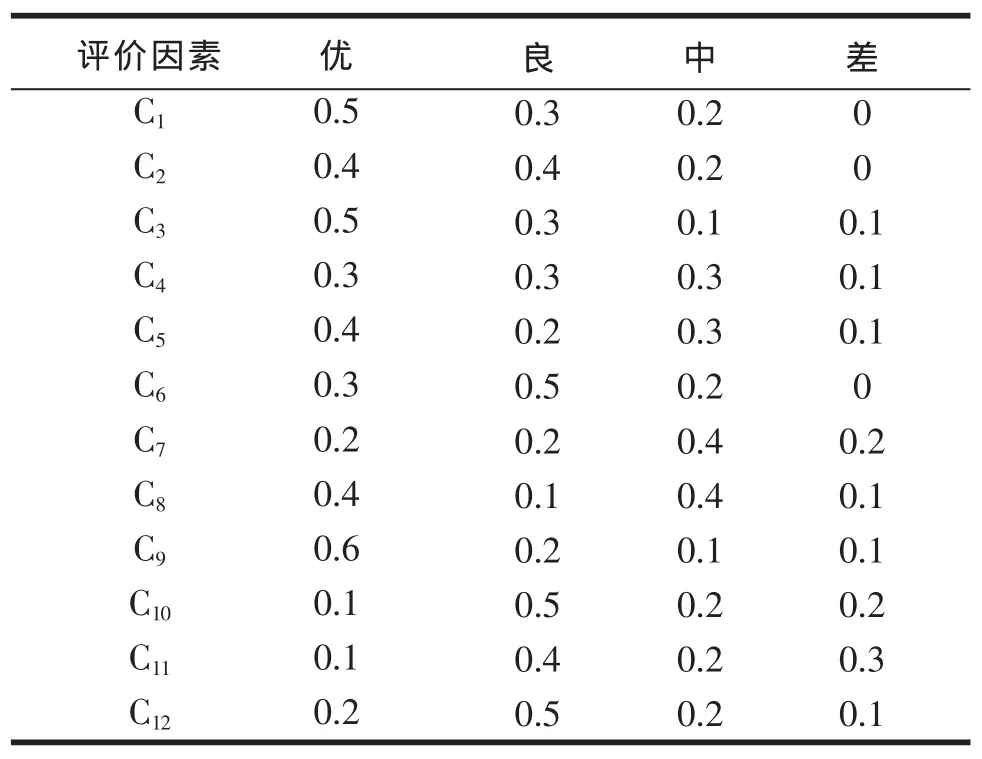
表10　專家打分表

根據表10，可以得出如下評價因素B1的模糊綜合評判結果：

同理可得：

由以上計算結果可以得出實訓課程綜合評判結果

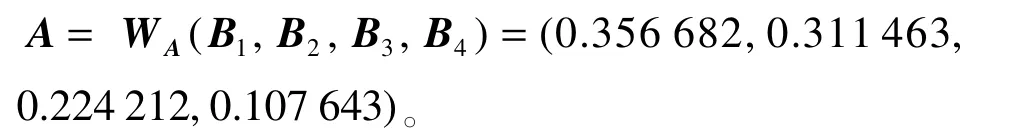
綜合評判結果顯示，課程評價結果為優、良、中、差的隸屬度分別為0.356 682,0.311 463,0.224 212 和0.107 643,其中最大值是0.356 682，根據最大隸屬度原則［8］，可以認定課程總體評價為優。

4　結束語

在本文中，我們以高職院校的一門實訓課為研究對象，建立了評價系統的遞階層次結構，利用改進冪法求得了各評價因素的相對權重，并在此基礎上對目標方案進行了綜合評定。結果顯示：通過改進的模糊層次分析法，我們可以得到更精確的評價結果。在實際操作中，我們選了12個課程評價因素，因此，無法體驗利用該方法求解時收斂速度的高效性。后續的研究將主要集中在以下兩個方面：一是課程指標體系構建的科學性和評價因素選取的全面性，二是如何通過改進計算機程序，進一步提高計算速度。

［1］崔繼賢，李月秋.改進的多層次分析法的研究及應用［J］.數學的實踐與認識，2014（14）：217-222．

［2］韓軍民，劉洪甫，李雪，等.模糊層次分析法在矩陣論教材評價方面的應用［J］.數學的實踐與認識，2012（16）：7-12．

［3］汪應絡.系統工程［M］.4版.北京：機械工業出版社，2008：120-123.

［4］張吉軍.模糊層次分析法（FAHP）［J］.模糊系統與數學，2000（2）：80-88.

［5］馮媛，蔡增玉，趙振宇，等.基于RFID的物流系統安全性研究［J］.制造業自動化，2014（1）：23-25.

［6］楊洋，吳志華.高職院校實訓課程效能評估指標的構建［J］.中國高等教育評估，2011（1）：42-45.

［7］徐澤水.AHP中兩類標度的關系研究［J］.系統工程理論與實踐，1999（7）：97-101.

［8］葉洪選，丁學平，陳華喜.高校畢業生就業質量評價方法研究：以銅陵學院為例［J］.陜西理工學院學報（自然科學版），2015（2）：73-78.

【責任編輯王云鵬】

Application of Improved FAHP in Evaluation of Practical Courses in Vocational College

WANG Baomin1，HUANG Shan2
（1.Department of Electronic Information Engineering，Anhui Business College，Wuhu 241002，China；2.Department of Economics and Management，Anhui Technical College of Mechanical and Electrical Engineering，Wuhu 241002，China）

The improved power method was introduced into FAHP in this paper，and the improved FAHP was proposed.Intermediate results of iteration were standardized，and the computing processes of FAHP were optimized.By eliminating the calculating steps of weight vectors of judgment matrix，the complicated consistency checking process was avoided and thus the computational efficiency was improved.On the background of practical training courses reform in vocational colleges，a scientific index evaluation system was constructed，the teaching effect was evaluated by improved FAHP，and the ideal calculating results were gotten.

fuzzy analytic hierarchy process（FAHP）；course evaluation；judgment matrix；improved power method

G712；N945.16

A

2095-7726（2016）09-0068-05

2015-03-16

安徽省教育廳教學研究項目（2014ZY119）；安徽省教育廳質量工程項目（2015mooc160）；安徽省教育廳質量工程項目（2015sjjd047）；安徽商貿職業技術學院教學研究項目（ZL201511）

王保敏（1984-），男，安徽天長人，碩士，研究方向：信息系統工程、決策支持。