求解索末菲爾德積分的廣義函數束方法
趙燕
(新鄉醫學院 生物醫學工程學院,河南 新鄉453003)
求解索末菲爾德積分的廣義函數束方法
趙燕
(新鄉醫學院 生物醫學工程學院,河南 新鄉453003)
應用廣義函數束方法求解了索末菲爾德積分。通過被積函數分式部分的指數擬合和索末菲爾德恒等式將無窮積分轉化為閉合級數形式,避免了貝塞爾函數值計算和數值積分中繁瑣的運算,提高了數值計算的效率和精度。
廣義函數束方法;索末菲爾德積分;指數擬合
目標識別是圖像處理、模式識別和計算機視覺領域的研究熱點,已廣泛應用于國民經濟、空間技術和國防等領域。在目標識別中,需要從目標的瞬態響應中提取目標的各種特征[1-3]。在實際操作中,要先精確提取含有衰減因子和諧振頻率信息的目標極點,然后通過求解一個線性最小二乘問題可以得到極點所對應的留數[3]。普朗尼法是提取極點分布的一種常用算法[1–3],這一方法衍生出最小二乘普朗尼法、總體最小二乘普朗尼法和奇異值分解普朗尼法。利用這些算法求極點分布的過程分為兩步:第一步是求解一個矩陣方程,第二步是通過尋找一個多項式的根求得極點分布。
近年來,在函數束方法[4]基礎上發展起來的廣義函數束法已成為一種比較流行的算法。與上面提到的幾種方法相比,該方法具有高魯棒性和高抗噪性,其優點是通過求解一個廣義特征值問題就可得到極點分布。
索末菲爾德積分的概念自提出以來,一直受到廣大數學研究人員的關注。研究人員一直致力于導出它的各種近似公式,近年來,他們更關心如何通過計算機求菲爾德積分問題的解。由于被積函數的奇異性和高震蕩性,如果采用傳統的變步長修正辛普生法或龍伯格法,不僅積分的計算費時,而且計算結果也經常出現不收斂或達不到精度等現象。如果計算多點積分,這些方法要求的計算量更大,其后果是計算時間更長,計算效率更低。
在本文中,筆者通過廣義函數束方法對被積函數的分式部分進行指數擬合,并利用索末菲爾德恒等式將無窮積分轉化為閉合級數形式,避免了貝塞爾函數值計算和數值積分中繁瑣的運算,提高了計算效率和計算精度。
1 廣義函數束方法
瞬態電磁信號為

其中,bi是復留數,si是復極點,δk是抽樣間隔。
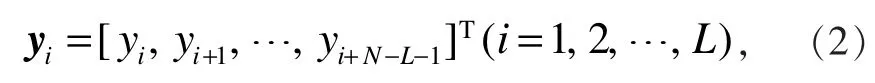
定義矩陣Y1和Y2為
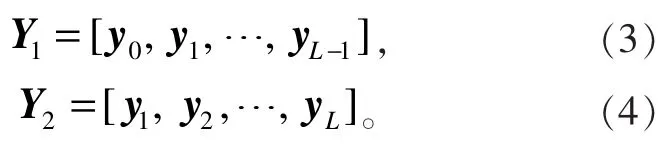
為了分析這兩個矩陣的底層構造,把它們改寫成

其中,

從矩陣Y1和Y2的分解結果可以看出:如果M≤ L≤N?M,矩陣束Y1的廣義特征值[6]就是待求極點,即為矩陣的秩,當L=M時,該方法將與函數束方法等同。對于廣義函數束方法,更需關注的是M 為了給出計算矩陣束廣義特征值的方法,記 其中,上標+和-1分別表示矩陣的偽逆和逆。 一般的索末菲爾德積分式為 取n=0時,由索末菲爾德恒等式 擬合,即 式(13)就有閉式表達式 筆者利用自己設計的計算機程序對廣義函數束方法進行了模擬。圖1是時,I0的計算結果。從圖1可以看出,廣義函數束方法與變步長辛普生法的計算結果相當吻合,計算所需要的時間更短。同樣計算60個點,廣義函數束方法耗時4.012 s,變步長辛普生法耗時620.128 s。 圖1 廣義函數束方法和變步長辛普生法的計算結果 [1]VAN BLARICUM M,MITTRA R.A Technique for Extracting the Poles and Residues of System Directly from Its Transient Response[J].IEEE Transactions on Antennas and Propagation,1975,23(6):777-781. [2]POGGIO A J,BLARICUM M L,MILLER E K,et al. Evaluation of a Processing Technique for Transient Data[J]. IEEE Transactions on Antennas and Propagation,1978,26(1):165-173. [3]VAN BLARICUM M,MITTRA R.Problems and Solutions Assocsiated with Prony's Method for Processing Transient Data[J].IEEE Transactions on Antennas and Propagation,1978,26(1):174-182. [4]HUA Y B.On Techniques for Estimating Parameters of Exponentially Damped/Undamped Sinusoids in Noise[D]. New York:Syracuse University,1988. [5]JAIN V K,SARKAR T K,WEINER D D.Rational Modeling by Pencil-of-function Method[J].IEEE Transactions on ASSP,1983,31(3):564-573. [6] ROY R,KAILATH T.ESPRIT-estimation of Signal Parameters Via Rotational Invariance Techniques[J].IEEE Transactions on Acoust,1989,7:984-995. 【責任編輯王云鵬】 Generalized Pencil-of-function Method for Solving Sommerfeld Integral ZHAO Yan Generalized pencil-of-function method was applied to calculate Smmmerfeld integral in this paper.Infinite integral could be changed into a closed form of accumulation by exponential fit of the integrand fraction and Sommerfeld identical equation so as to avoid tedious computation of Bessel function evaluation and numerical integration.The computational efficiency and accuracy were greatly improved. generalized pencil-of-function method;Sommerfeld integral;exponential fit O177.2 A 2095-7726(2016)09-0008-03 2016-03-25 趙燕(1980-),女,河南濮陽人,講師,碩士,研究方向:計算數學。



2 索末菲爾德積分的數值計算
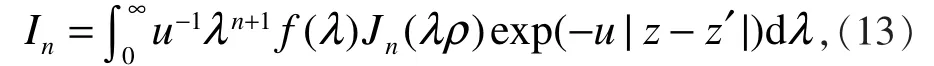



3 模擬結果

(School of Biomedical Engineering,Xinxiang Medical University,Xinxiang 453003,China)

