巴拿赫格上的幾乎弱*Dunford-Pettis算子

馮夏男，陳滋利

（西南交通大學 數學學院，成都610031）

巴拿赫格上的幾乎弱*Dunford-Pettis算子

馮夏男，陳滋利

（西南交通大學 數學學院，成都610031）

研究了巴拿赫格上的幾乎弱*Dunford-Pettis算子及其性質，利用相對弱緊集給出了幾乎弱*Dunford-Pettis算子的等價刻畫。在巴拿赫格有序連續范數及強GP（強DPrcP）性質或者對偶巴拿赫格有弱單位的前提下，證明了幾乎弱*Dunford-Pettis算子為幾乎極限全連續算子（幾乎Dunford-Pettis全連續算子）。

幾乎極限集；相對弱緊集；強GP性質；幾乎弱*Dunford-Pettis算子

在巴拿赫格及其算子理論的研究中，人們更關注算子所在空間的性質和算子本身的性質，而特殊算子類的性質一直是重要的研究內容。

幾乎弱*Dunford-Pettis算子［1］是隨著幾乎弱Dunford-Pettis算子［2］和弱*Dunford-Pettis算子［3］的出現而產生的。DENG Yang等［1］用不交序列刻畫了此類算子，并得出了此類算子與其他特殊算子的關系。CHEN Jinxi等［4］借助相對弱緊集刻畫了此類算子，通過幾乎弱*Dunford-Pettis算子把相對弱緊集映成幾乎極限集，并通過巴拿赫格中算子的性質得出了幾乎弱*Dunford-Pettis算子與幾乎極限全連續算子、幾乎Dunford-Pettis全連續算子之間的關系。在此基礎上，我們研究了巴拿赫格上的幾乎弱*Dunford-Pettis算子及其性質，給出了它們的等價刻畫，并在巴拿赫格有序連續范數及強GP（強DPrcP）性質或者對偶巴拿赫格有弱單位的前提下，證明了幾乎弱*Dunford-Pettis算子為幾乎極限全連續算子（幾乎Dunford-Pettis全連續算子）的結論。

1　幾乎弱*Dunford-Pettis算子的刻畫

定義1［1］：設E和F為巴拿赫格，如果對不交的弱零序列和不交的弱*零序列′,有,則稱T: E→F為幾乎弱*Dunford-Pettis算子。

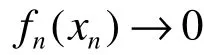
定義 2［1］：設 E為巴拿赫格，若對不交的弱零序列和不交的弱*零序列′,有 ,則稱巴拿赫格E具有幾乎弱*Dunford-Pettis性質，也簡稱E具有aw*DP性質。

定理1：在σ-Dedekind完備的巴拿赫格E上，下列結論是等價的：1）E的每一個相對弱緊集的實體包是幾乎極限集；2）對于每一個不交的弱零序列{xn}，子集是幾乎極限集；3）E具有aw*DP性質。

證明：先證結論1）推出結論2）。設{xn}為E上不交的弱零序列，則集合顯然是E上的相對弱緊集。又由已知條件可知，集合是幾乎極限集。

再證結論2）推出結論3）。對于E′上每一個不交的弱*零序列{fn}，有，則由不等式可得E具有aw*DP性質。

最后證結論3）推出結論1）。令A′為E上的相對弱緊集，A為A′的實體包。由文獻［5］中定理4.34可知，對于A中不交序列{zn}，有。由以上證明過程可知，對于E′中不交弱零序列{gn}和A中不交序列，故由文獻［4］中定理2.5可知A是幾乎極限集。

巴拿赫格上的極限算子顯然是幾乎極限算子，也是弱緊算子，但反過來結論是不成立的。例如，弱緊算子不是幾乎極限算子，也不是弱緊算子，但Idl∞卻是幾乎極限算子。

推論1：在σ-Dedekind完備巴拿赫格E上，下列結論是等價的：1）E具有aw*DP性質；2）是幾乎弱*Dunford-Pettis算子；3）對于不交的弱零序列和不交的弱*零序列，有；4）對于不交的弱零序列和不交的弱*零序列，有；5）對于不交的弱零序列和不交的弱*零序列有

下面我們給出判斷任意算子為幾乎弱*Dunford-Pettis算子的充分必要條件。

定理2：設E和F為巴拿赫格，其中E是σ-Dedekind完備的，則對于算子T: E→F，下列結論是等價的：1）T是幾乎弱*Dunford-Pettis算子；2）T把E中相對弱緊子集映成F中幾乎極限集子集；3）如果S是把巴拿赫格G映射到E的弱緊算子，則T°S是幾乎極限算子；4）若S是l1到E的弱緊算子，則T°S是幾乎極限算子。

再證結論2）推出結論3）。設S:G→E為弱緊算子，S( BZ)是E的相對弱緊子集，則由已知條件可知是F的幾乎極限集，因而T°S是幾乎極限算子。

結論3）推出結論4）是顯然的。

最后用反證法證結論4）推出結論1）。設存在E上的不交弱零序列{xn}，F′上的不交弱*零序列{fn}和正數ε，使得

考慮算子S:l1→X，且定義S為，其中為l1中的任一序列。由文獻［5］中定理5.26可知S是弱緊的，因此T°S是幾乎極限算子，故對任意n∈N，有不等式，其中是l1的一組基。這與已知條件矛盾，因此結論成立。

定義3［5］：如果巴拿赫格E上每一個正的弱零序列依范數收斂于零（每一個不交的弱零序列依范數收斂于零），則稱巴拿赫格E具有正Schur性質（Schur性質）。

定義4［6］：如果每一個弱*零序列依范數收斂于零，則稱巴拿赫格E具有對偶Schur性質。

定理3：設巴拿赫格E具有序連續范數，則E具有aw*DP性質的充分必要條件是E具有正Schur性質。

證明：先證必要性。假設E具有正Schur性質，則E+中弱零序列依范數收斂于零，故E具有aw*DP性質。

定理4：設巴拿赫格E和E′具有序連續范數，則E具有aw*DP性質的充分必要條件是E具有正對偶Schur性質。

證明：先證必要性。假設E具有正對偶Schur性質，則E中弱零序列是范數有界序列，故E具有aw*DP性質。

顯然，每一個具有DP*性質的巴拿赫格也具有aw*DP性質，但該結論反過來不一定成立。例如，是具有aw*DP性質的σ-Dedekind完備的巴拿赫格，但具有正Schur性質卻不具有DP*性質，具有DP*性質的可分巴拿赫空間一定具有Schur性質。

由文獻［1］中定理2.6可以得出下列推論，該推論給出了aw*DP性質與DP*性質等價的充分必要條件。

推論2：巴拿赫格E具有aw*DP性質與E具有DP*性質等價，只需下列條件之一成立：1）E有弱序列連續格運算，2）F′有弱*序列連續格運算，3）F有弱序列連續格運算。

2　幾乎弱*Dunford-Pettis算子與幾乎極限全連續算子之間的聯系

定義5［8］：設T是從巴拿赫格E到巴拿赫空間Y的有界線性算子，如果E中弱零序列和幾乎極限序列依范數收斂于零，則稱T為幾乎極限全連續算子。

定義6［9］：設T是從巴拿赫格E到巴拿赫空間Y的有界線性算子，如果E中弱零序列和幾乎Dunford-Pettis序列依范數收斂于零，則稱T為幾乎Dunford-Pettis全連續算子。

定理5［8］：設巴拿赫格E和E′有弱單位或E有序連續范數，則下列結論是等價的：1）E有強GP性質；2）對于巴拿赫格F，有aLcc(E, F)=L( E, F)；3），其中aLcc為幾乎極限全連續算子的簡稱。

我們知道，幾乎弱*Dunford-Pettis算子是存在的，但它不是幾乎極限全連續算子。例如，恒等算子是幾乎弱 *Dunford-Pettis算子（因為具有幾乎弱*Dunford-Pettis性質），但不是幾乎極限全連續算子（因為不具有強GP性質）。

以下結論將說明巴拿赫格上的幾乎弱*Dunford-Pettis算子是幾乎極限全連續算子。

定理6：若巴拿赫格E、E′有弱單位或E有序連續范數，巴拿赫格F具有aw*DP性質，則下列結論是等價的：1）每一個幾乎弱*Dunford-Pettis算子T: E→F是幾乎極限全連續算子；2）E有強GP性質。

證明：先用反證法證結論1）推出結論2）。假設E不具有強GP性質，只需證明幾乎弱*Dunford-Pettis算子T：E→F不是幾乎極限全連續算子即可得出結論。由于E不具有強GP性質，則E中存在一個滿足的弱零幾乎極限序列，其中

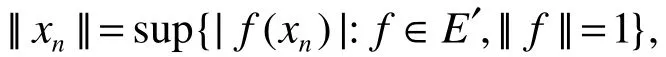
再證結論2）推出結論1）。設E是使E′具有序單位的巴拿赫格或E具有序連續范數，則由文獻［8］中推論2.15可知，E具有強GP性質的充分必要條件是E中每一個弱零序列和幾乎極限序列都依范數收斂于零，因而該條件下的每一個算子都是幾乎極限全連續算子。

定理7：設巴拿赫格E、E′有弱單位或E有序連續范數，且σ-Dedekind完備的巴拿赫格F具有aw*DP性質，則下列結論是等價的：1）每一個幾乎弱*Dunford-Pettis算子T：E→F是幾乎極限全連續算子；2）F是離散的具有序連續范數的巴拿赫格。

證明：先證結論1）推出結論2）。由定理6可知F具有強GP性質，且F是σ-Dedekind完備的，則由文獻［5］中定理2.3可知F是離散的具有序連續范數的巴拿赫格。

再證結論2）推出結論1）。由文獻［8］中推論3.5可知，離散的具有序連續范數的巴拿赫格上每一個有界線性算子都是幾乎極限全連續算子。

如果E′沒有弱單位，且E不具有序連續范數，定理6、定理7就可能不成立。事實上，C( K)中每一個弱零的幾乎極限序列依范數收斂于零（K是緊Hausdorff空間），因此C( K)上每一個算子都是幾乎極限全連續算子，但是C( K)不具有強GP性質。

推論3：設巴拿赫格E、E′有弱單位或E有序連續范數，則下列結論是等價的：1）每一個幾乎弱*Dunford-Pettis算子T：E→l∞都是幾乎極限全連續算子；2）E有強GP性質。

推論4：設σ-Dedekind完備的巴拿赫格F、F′有弱單位或E有序連續范數，則下列結論是等價的：1）每一個幾乎弱*Dunford-Pettis算子T: l∞→F 都是幾乎極限全連續算子；2）F是離散的具有序連續范數的巴拿赫格。

定義7［5］：如果E+中遞增的范數有界序列是依范數收斂的，則稱巴拿赫格E為KB空間。

若E為巴拿赫格，則E為離散的KB空間的充分必要條件是E具有強DPrcP性質［9］。可以確定一個算子，使得幾乎弱*Dunford-Pettis算子為幾乎Dunford-Pettis全連續算子，該結論的證明過程同定理6和定理7。

推論5：設巴拿赫格E、E′有弱單位或E有序連續范數，則下列結論是等價的：1）每一個幾乎弱*Dunford-Pettis 算子T: E→l∞都是幾乎Dunford-Pettis全連續算子；2）E有強DPrcP性質。

推論6：設巴拿赫格F、F′有弱單位或有序連續范數，則下列結論是等價的：1）每一個幾乎弱*Dunford-Pet tis算子T: l∞→F都是幾乎Dunford-Pettis全連續算子；2）F是離散的KB空間。

［1］DENG Y，CHEN Z，GAO N.On Positive Almost Weak *Dunford-Pettis Operators［J］.Positivity，2015，20（2）：283-294.

［2］KHALID B，MOHAMMED M.On the Class of Positive Almost Weak Dunford-Pettis Operators［J］.Positivity，2013，17（3）：589-600.

［3］H'MICHANE J，ELKADDOURIl A，BOURAS K，et al. On the Class of Limited Operators［J］.Acta Mathematica Uinversitatis Comeniance，2016，85（2）：191-196.

［4］CHEN J X，CHEN Z L，JI G X.Almost Limited Sets in Banach Lattices［J］.Journal of Mathematical Analysis and Applications，2014，412（1）：547-553.

［5］ALIPRANTIS C D，BURKINSHAW O.Positive Operators ［M］.Netherlands：Springer，2006：207-252.

［6］AQZZOUZ B，ELBOUR A，WICKSTEAD A W.Positive Almost Dunford-Pettis Operators and Their Duality［J］. Positivity，2011，15（2）：185-197.

［7］MEYER-NIEBERG P.Banach Lattices［M］.Berlin：Springer，1991：87-99.

［8］HALIMEH A，MOHAMMAD M，SADEGH M.The Strong Gelfand-Phillips Property in Banach Lattices［J］.Journal of Mathematical Analysis and Applications，2016，10（1）：15-26.

［9］ARDAKANI H，SADEGH MODARRES MOSADEGH S M.Strong Relatively Compact Dunford-Pettis Property in Banach Lattices［J］.Annals of Functional Analysis，2016，7（2）：270-280.

【責任編輯王云鵬】

Almost Weak*Dunford-Pettis Operators on Banach Lattices

FENG Xianan，CHEN Zili
（School of Mathematics，Southwest Jiaotong University，Chengdu 610031，China）

The almost weak*Dunford-Pettis operators on Banach lattice was studied in this paper.The characteristics of almost weak*Dunford-Pettis operators and its equivalent properties based on relatively weakly compact sets were given.It was proved that almost weak*Dunford-Pettis operators were almost limited completely continuous operators（almost Dunford-Pettis completely continuous operators）under the preconditions that Banach lattice had order continuous norm or its dual Banach lattice had weak unit，if the Banach lattice had strong GP property（strong DPrcP property）.

almost limited sets；relatively weakly compact sets；the strong Gelfand-Phillips property；almost weak*Dunford-Pettis operator

O177

A

2095-7726（2016）09-0004-04

2016-05-14

馮夏男（1990-），女，河南新鄉人，碩士，研究方向：泛函分析與線性算子理論。