一種求解分段常數Robin系數的數值方法

馬衍波

（韓山師范學院數學與統計學院，廣東潮州　521041）

一種求解分段常數Robin系數的數值方法

馬衍波

（韓山師范學院數學與統計學院，廣東潮州521041）

考慮分段常數的Robin反問題的數值求解，由于TV正則化泛函在0點不可導，其數值算法的設計是很大的挑戰.文章給出一種自適應的TV泛函，該泛函綜合了Tikhonov正則化方法和TV正則化方法的優點.數值實驗表明，該方法對分段常數的Robin反問題的恢復有較好的效果.

Robin系數；Tikhonov正則化；反問題

考慮Laplace方程的Robin邊界問題

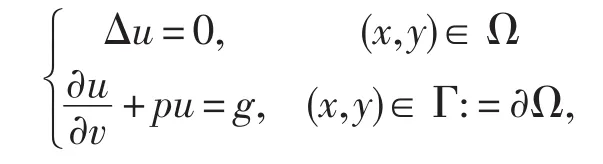
帶有Robin邊界條件的Laplace方程可用來刻畫眾多實際應用，如對穩態熱傳導建模或在半導體研究中模擬金屬硅之間的導電性.關于其理論及數值研究已吸引眾多學者關注［1，2］.相對于正問題，若已知u在部分邊界上的值u0=u|Γ，其中Γ0?Γ，且Γ0?Γ1=Φ.重構恢復Robin系數p的過程就構成

0了一個反問題，稱為Robin反問題.該反問題來源于半導體裝置［3，4］、各種無傷檢測［5-7］.

Robin反問題是一個不適定問題，即使觀測數據的微小變化，也會造成恢復數據的巨大變化，即解不連續依賴于給定數據.由于其不適定性，該問題的研究充滿了挑戰性，幾十年來對其理論研究和數值算法已取得了眾多成果［8-14］.而針對非光滑的Robin系數，基于全變差的非線性反問題的數值方法得到了很多學者的重視［15-18］.

由于TV正則化泛函在0點不可導，所以其數值算法的設計是很大的挑戰.考慮到Tikhonov正則化方法和TV正則化方法的優缺點，給出一種自適應的TV方法，將Tikhonov正則化方法和TV正則化方法的優點結合起來.數值實驗表明，該方法對分段常數的Robin反問題的恢復有較好的效果.

1　邊界積分方程及其離散化

首先，引入令?=?（x,y）為二維Laplace方程的基本解，由格林公式，得到如下積分方程

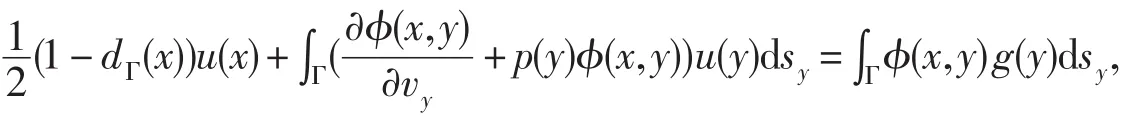
該積分方程含有dΓ（x）是定義在邊角上的指標函數，滿足

定義

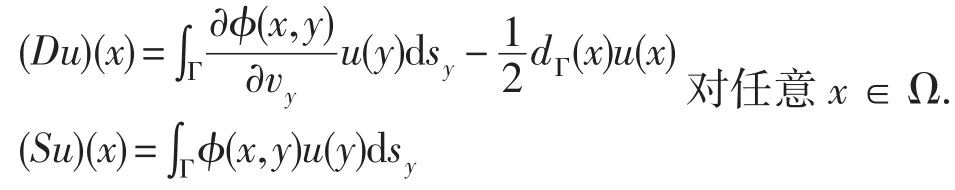
假定平面域的邊界Γ為光滑的，即設Γ=｛z（t）：t∈［0,1］｝,其中，z：R→R2為2π周期光滑函數，且z為定義［0，1］上的單射函數，滿足z'（t）≠0,?t∈［0,1］.令

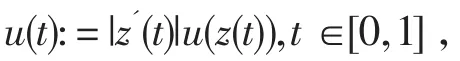
可得到參數化的積分算子

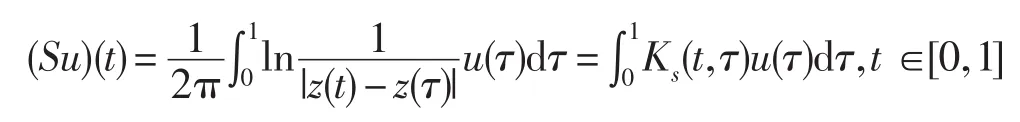
及

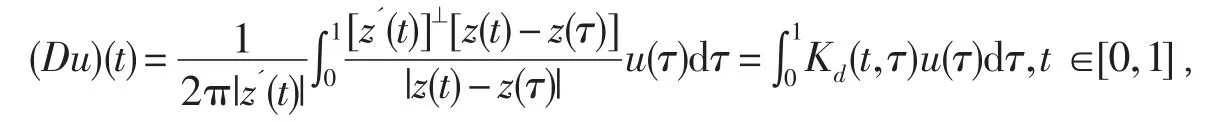
其中，對向量a=（a1,a2），有a⊥=（a2,-a1）.

用中點積分公式對積分進行離散并用中心差分商對導數進行近似.讓積分區間［0，1］被分為N等份［（i-1）h,ih］,i=1,2,…N，離散步長為h=1/N，則離散點為ti=（i-1/2）h,？i=1,2,…,N.假設

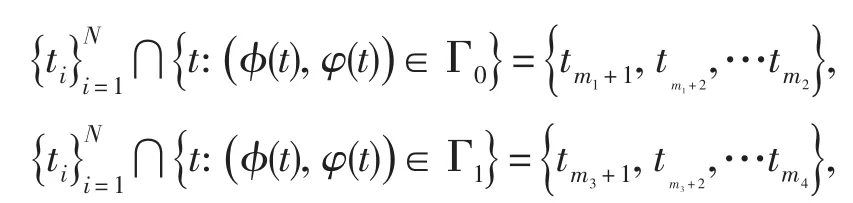
記u和p分別是Γ上的函數u（t），Γ1上的函數p（t）的離散形式，它們分別為

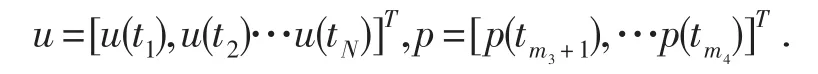
記離散數據為

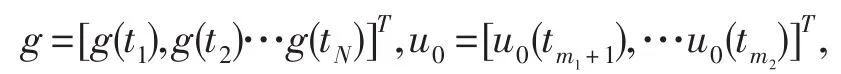
用中點積分公式進行離散，分別記積分核函數Kd和Ks的離散矩陣為D和S.故而算子方程式的離散形式為

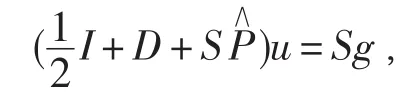
2　自適應泛函

其中

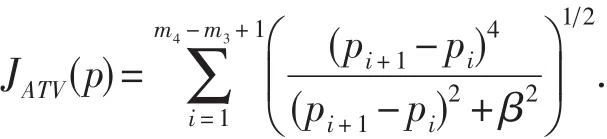
注意：這里的pi是p（ti）的近似值，且p0=0，pm4-m3+1=0.

令

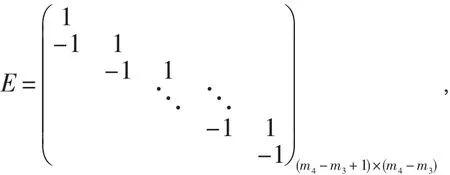
則有

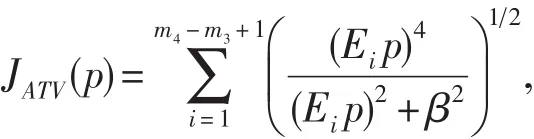
這里Ei表示矩陣E的第i行.

引進向量e（p）=R0A（p）-1f-u0，上述泛函（1）可以簡寫為殘差項和正則項之和

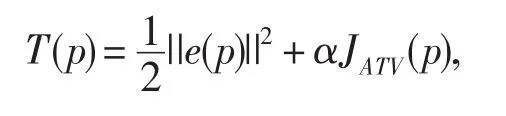
該正則泛函充分考慮了ROF模型和l2模型的優勢：當|pi+1-pi|?β，說明函數在該點處梯度變化較大，可能存在斷點，相應的正則分量接近|pi+1-pi|，可以充分利用TV正則的優勢處理斷點的恢復；而|pi+1-pi|?β說明函數在該點處梯度變化不大，此時相應的正則分量接近||pi+1-pi||2/β，故此時可以充分利用l2范數模型的優勢，使得近似解具有一定的光滑性.

3　數值實驗

利用高斯牛頓法討論橢圓域上的Robin反問題的數值恢復.在本實驗中，設其具有標準參數表示

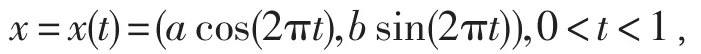
實驗中固定a=1，b=0.2.分別給定Γ0及Γ1為

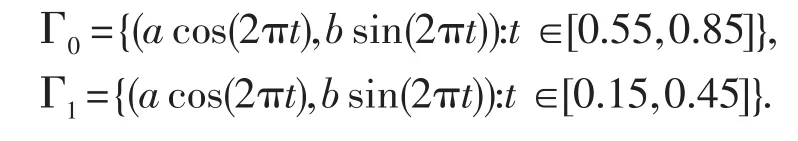
函數g（t）為

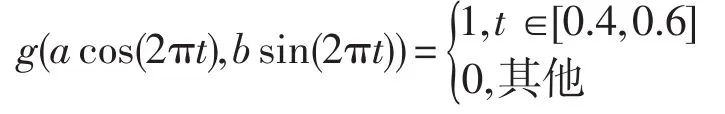
在本實驗中，選擇有兩個斷點和三個斷點的分段常數的Robin參數分別為p1（t）和p2（t）.具體如下

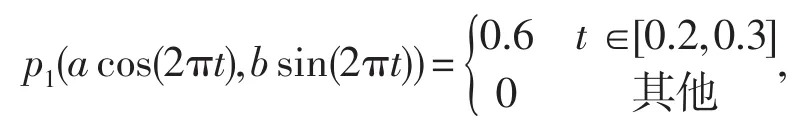
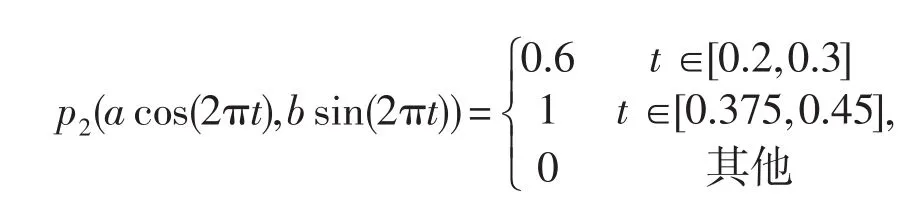
考慮不同噪聲級數下的恢復情況，各實驗中正則參數α的選取由偏差原理給出.給出了不同噪聲水平下的系數恢復情況.

當所給噪聲級別δ=5%時不同情形下的恢復效果見圖1，其中對左圖的恢復經過55次迭代，相對誤差為1.3%，而對右圖經過70次迭代，相對誤差為1.6%.

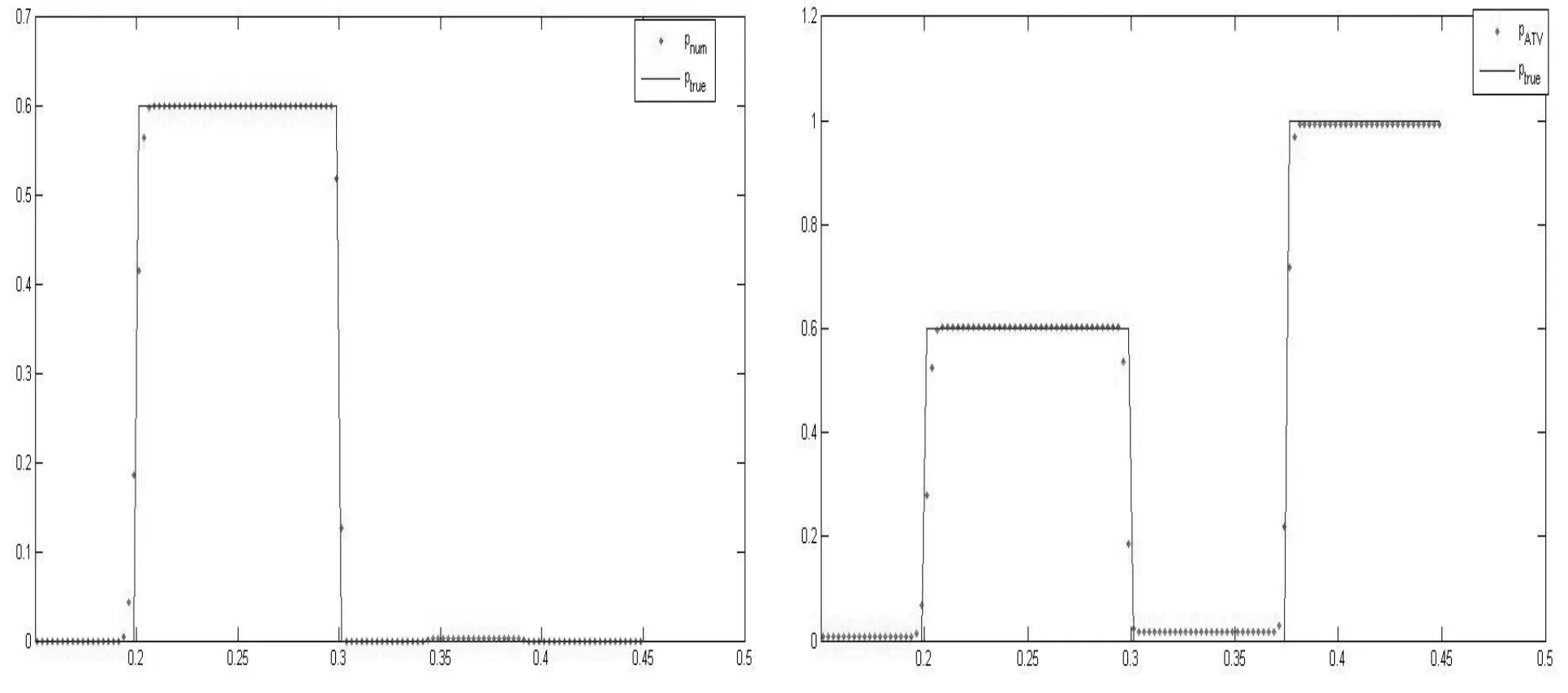
圖1　噪聲級別δ=5%時的恢復效果

當所給噪聲級別δ=10%時不同情形下的恢復效果見圖2，其中對左圖的恢復經過86次迭代，相對誤差為2.1%，而對右圖經過90次迭代，相對誤差為3%.

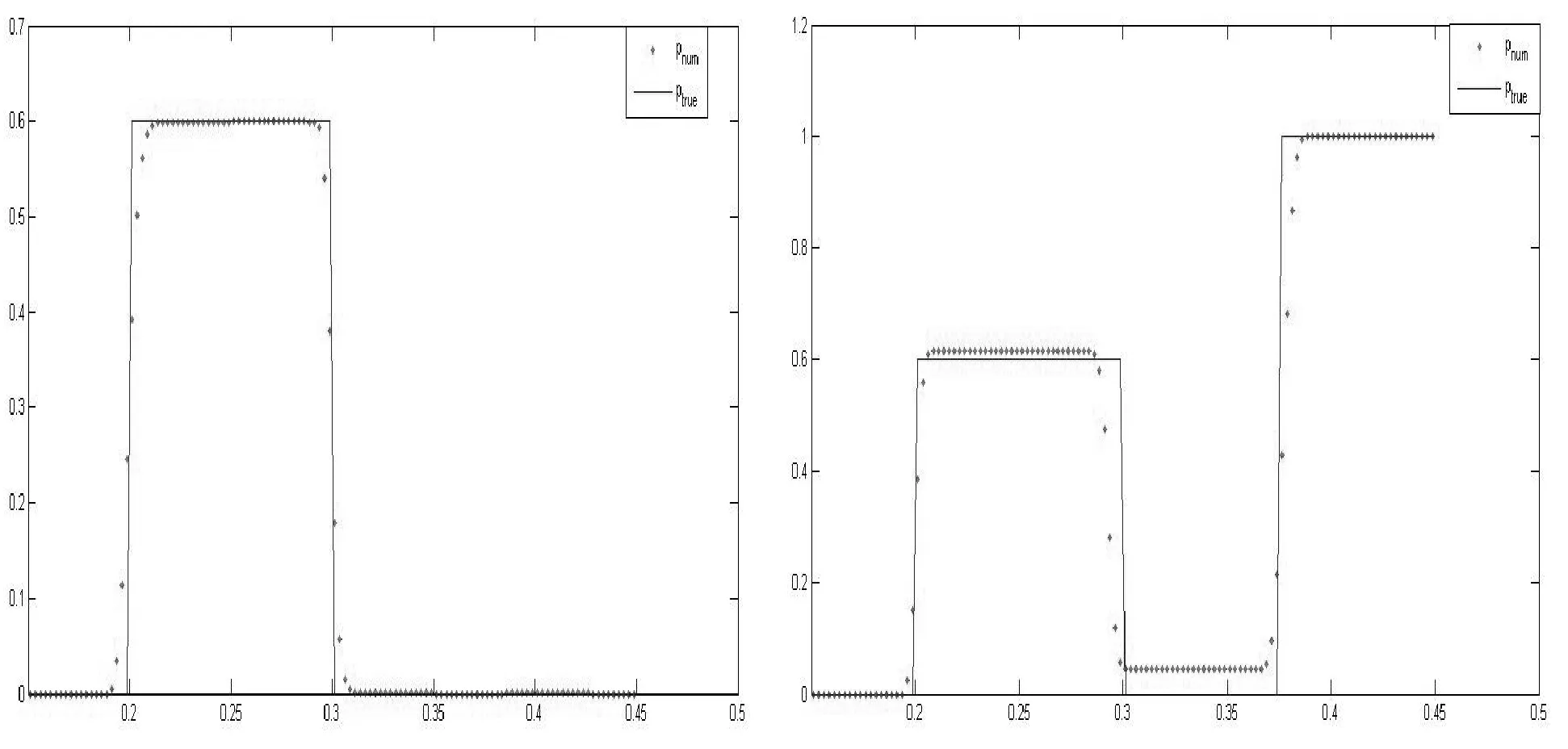
圖2　噪聲級別δ=10%時的恢復效果

當所給噪聲級別δ=15%時不同情形下的恢復效果見圖3，其中對左圖的恢復經過100次迭代，相對誤差為4.3%，而對右圖經過113次迭代，相對誤差為5.2%.

圖3　噪聲級別δ=15%時的恢復效果

4　結論

自適應的TV泛函充分考慮了TV模型和l2模型的優勢，在可能存在斷點的地方，充分利用TV正則的優勢處理斷點的恢復；而在不是斷點的地方，可以充分利用l2范數模型的優勢，使得近似解具有一定的光滑性.數值實驗也說明了這一點.

［1］BUSENBERG S,FANG W.Identification of semiconductor contact resistivity［J］.Q Appl Math，1991，49（4）：639-649.

［2］LOH W，SWIRHUN S，SCHREYER T.Modeling and measurement of contact resistances［J］.Electron Devices，IEEE，1987，114（3）：512-524.

［3］FANG W，ZENG X.A direct solution of the Robin inverse problem［J］.J Inte Equa App，2009，4（21）：545-557.

［4］JIN B，ZOU J.Inversion of Robin coefficient by a spectral stochastic finite element approach［J］.J Comp Physl，2008，227 （6）：3282-3306.

［5］KABANIKHIN S，KARCHEVSKY A.Optimizational method for solving the Cauchy problems for an elliptic equation［J］.J Inv Ill-Posed Problems，1995，3（3）：21-46.

［6］KAUP PG，SANTOSA F.Nondestructive evaluation of corrosion damage using electrostatic measurements［J］.J Nondestruct Eval，1995，14（14）：127-136.

［7］FANG W，ZENG X.Recover of an interface from boundary measurement in an elliptic differential equation［J］.Adv Com Math，2012，36（2）：201-220.

［8］FANG W，ZENG X.Numerical recovery of Robin boundary from boundary measurements for the Laplace equation［J］.J Comp App Math，2009，24（24）：573-580.

［9］ITO K，JIN B.A new approach to nonlinear constrained Tikhonov regularization［J］.Inverse Problems，2011，27（10）：977-994.

［10］JIN B.Conjugate gradient method for the Robin inverse problem associated with the Laplace equation［J］.Int J Numer Math Engng，2007，71（4）：433-453.

［11］JIN B，LU X.Numerical identification of a Robin coefficient in parabolic problems［J］.Math Comp，2012，81（279）：1369-1398.

［12］VOGELIUS M，XU J.A nonlinear elliptic boundary value problem related to corrosion modeling［J］.Q Appl Math，1998，56：479-505.

［13］YANG F，YAN L，WEI T.The identification of a Robin coefficient by a conjugate gradient method［J］.Int J Numer Math Engng，2005，78（7）：800-816.

［14］LIN F，FANG W.A linear integral equation approach to the Robin inverse problem［J］.Inverse Problems，2005，21（5）：1757-1772.

［15］JIN B，ZOU J.Numerical estimation of piecewise constant Robin coefficient［J］.SIAM J Control Optim，2009，48（3）：1997-2002.

［16］JIN B，MAASS P J.Sparsity regularization for parameter identification problems［J］.Inverse Problems，2014，28（12）：1-70.

［17］RAINER K，WILLIAM R.Nonlinear integral equation and iterative solution for an inverse boundary value problem［J］.Inverse Problems，2009，27（2）：1207-1223.

［18］SANTOSA F，VOGELIUS M，XU J.An effective nonlinear boundary condition for corroding surface identification of damage based on steady state electricdata［J］.Z Angew Math Phys，2009，49（4）：656-679.

Numerical Method of Piece-wise Constant Robin Coefficient

MA Yan-bo
（School of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong，521041）

In this paper，we consider a numerical method for reconstructing piecewise constant Robin coefficients.A novel adaptive Total Varition functional is proposed based on the Tikhonov functional and Total Varition functional.The numerical expriments are presented to illustrate its distinct features.

Robin coefficient；Tikhonov regularition；inverse problems

O 241.82

A

1007-6883（2016）03-0023-06

責任編輯朱本華

2016-01-14

國家自然科學基金（項目編號：11271238）.

馬衍波（1978-），男，山東巨野人，韓山師范學院數學與統計學院講師，博士.