Navier-Stokes方程耦合Smoluchowski方程在三維空間中的整體強解

黃丙遠

（韓山師范學院數學與統計學院，廣東潮州　521041）

Navier-Stokes方程耦合Smoluchowski方程在三維空間中的整體強解

黃丙遠

（韓山師范學院數學與統計學院，廣東潮州521041）

考慮一類Navier-Stokes-Smoluchowski方程組在有界光滑區域Ω?R3中的初邊值問題.利用Ballew在其博士論文中得到的局部強解，對強解建立一系列與時間無關的先驗估計，最后得到此模型的整體強解.

Navier-Stokes方程；Smoluchowski方程；強解；整體性

流體與粒子相互作用模型在工業過程中有許多應用，例如在生物技術、醫藥、廢水回收、礦物加工中出現粒子在流體中分散懸浮的沉淀現象，空氣問題中涉及到的污染現象，還有活性液體形成的燃燒現象等［1-4］，并且已經引起一些數學學者的注意［5-7］.

在有界光滑區域Ω?R3中，本文考慮的一類流體與粒子相互作用模型是Navier-Stokes系統耦合粒子在液體中進化所產生的Smoluchowski方程

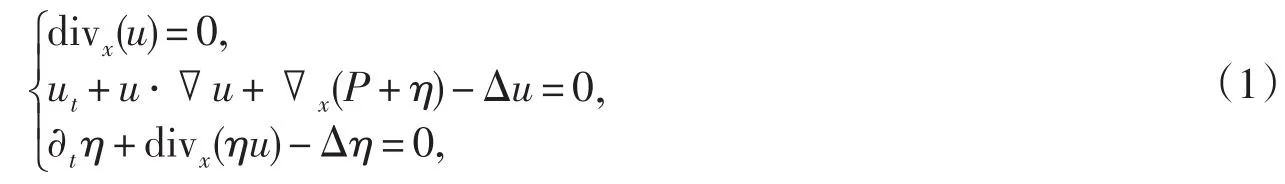
其中流體速度 u=u（x,t）=（u1,u2,u3）.Ω×［0,∞）→R3,粒子密度 η=η（x,t）：Ω×［0,∞）→R1，壓力函數P=P（x,t）：Ω×［0,∞）→R1.

關于問題（1），它是可壓縮Navier-Stoke-Smoluchowski方程組［5-7］滿足ρ=M與外力項?Φ=0的情形.但在三維空間的整體解方面，可壓縮Navier-Stoke-Smoluchowski方程組還沒有相關的結果.

因此，文中將研究問題（1）在有界光滑區域Ω?R3中的整體強解，假設初值條件

與邊值條件

u|?Ω=0，?xη?n|?Ω=0，n表示在邊界?Ω上的單位外法向量，

1　先驗估計

對于問題（1）～（3）的局部強解，實際上Ballew在文獻［6］中已經得到了證明，具體如下：

定理1.1［6］若初值條件滿足H2,η0（x）∈H2，那么存在一個有限的時間T＜∞，使得問題（1）～（3）在Ω×［0, T］上有唯一的強解（u,η），且滿足

下面對（u,η）做先驗估計，建立一些與時間T無關的一致估計.另外，記常數M，僅依賴于初值（u0（x）,η0（x），而不依賴于u,η及時間T.

引理1.1（基本能量等式）對于任意時間T≥0，則

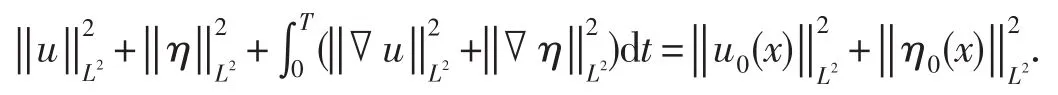
證明用u與方程（1）2做向量積，并在Ω上關于x積分，利用分部積分法，不可壓條件（1）1及邊界條件（3），得，在［0, T］上關于時間t積分，即

類似地，用η與方程（1）3做向量積，并在Ω上關于x積分，得

在［0,T］上關于時間t積分，即

聯立式（4）與（5），引理1.1證畢.

引理1.2對于任意時間T≥0，則

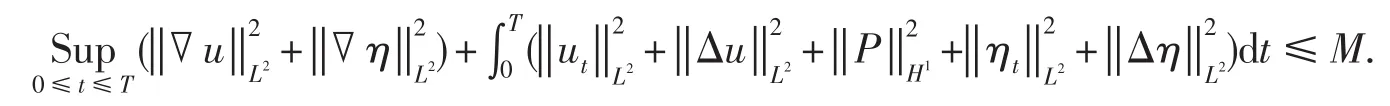
證明用ut與方程（1）2做向量積，并在Ω上關于x積分，利用不可壓條件（1）1與邊界條件（3），得 ,在［0, T］上關于時間t積分，得

對方程（1）2應用定常Stoke方程的LP理論［8］，利用式（6），得

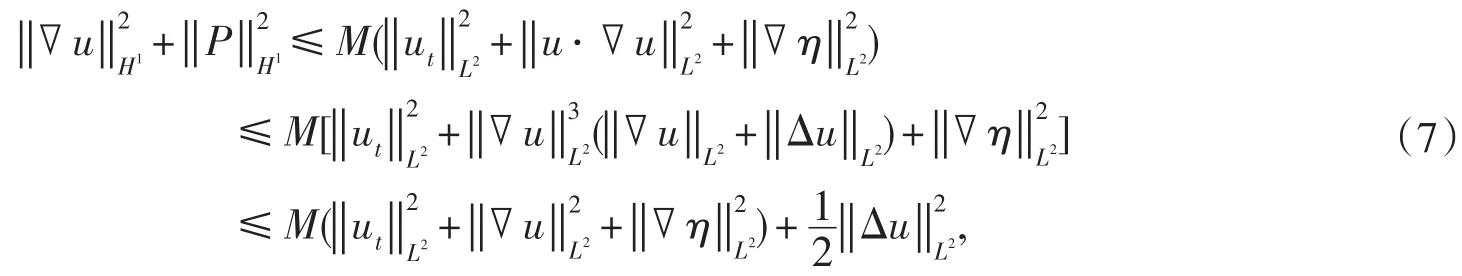
即

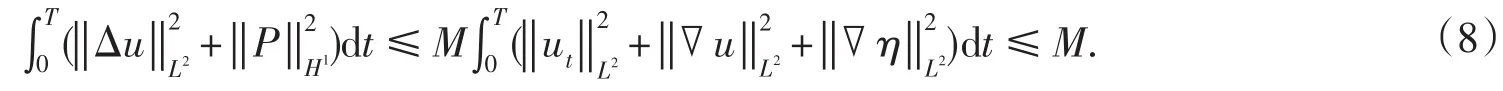
用Δη與方程（1）3做向量積，并在Ω上關于x積分，利用H?lder不等式與G-N不等式，Cauchy不等式，得

利用式（6），（7）及橢圓估計，上式變為

由引理1.1與式（8），對式（9）作用Gronwall不等式，得

對方程（1）3應用L2理論及H?lder不等式，得

即

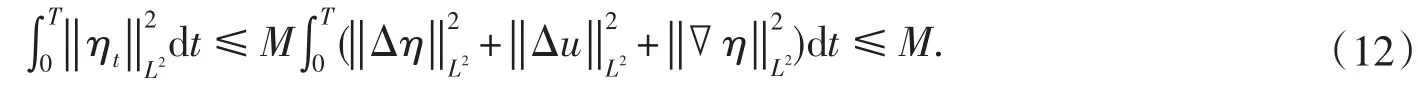
聯立式（6），（8），（10）及（12），引理1.2證畢.

引理1.3對于任意時間T≥0，則

證明對方程（1）2關于t求導，得utt+ut??u+u??ut+?x（Pt+ηt）-Δut=0.

用ut與方程（13）做向量積，在Ω上關于x積分，用不可壓條件（1）1與邊界條件（3），得

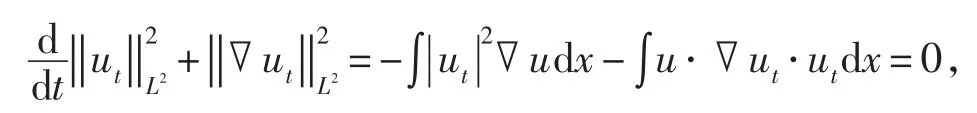
在［0,T］上關于時間t積分，對方程（1）2作用L2估計，得

由式（7），（14）及引理1.2，得

對方程（1）3關于t求導，得

用ηt與方程（16）做向量積，并在Ω上關于x積分，利用不可壓條件（1）1，H?lder不等式，G-N不等式，Cauchy不等式及式（10），得

即 ,并在［0, T］上關于時間t積分，利用式（11）與引理1.1～ 1.2，得

由方程（1）3及橢圓方程估計，得

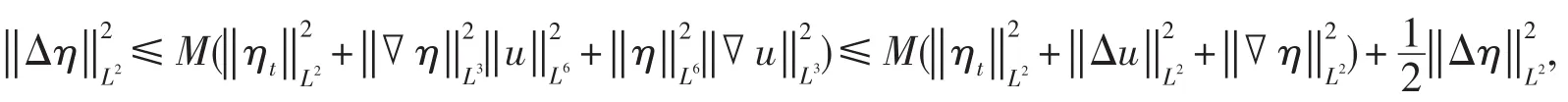
結合式（10）、（13）及（17），則上式可得到

因此，聯立式（14）、（15）、（17）及（18），引理1.3證畢.

2　整體強解

定理2.1若初值條件滿足u0（x）∈H01?H2,η0（x）∈H2，則問題（1）～（3）在Ω×［0,∞］上有唯一的整體強解（u,η），且滿足

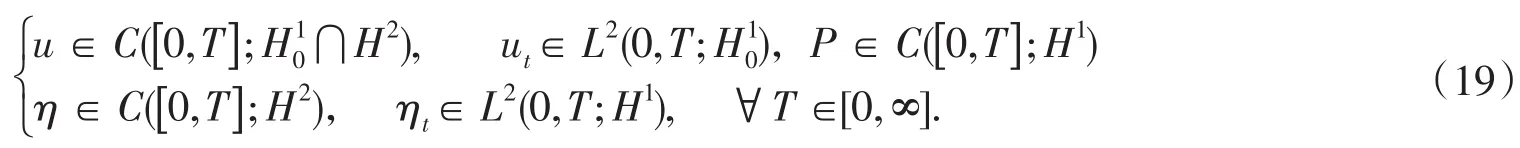
證明從第1部分中發現：存在某個有限時間T,（u,η）是問題（1）～（3）在Ω×［0,T］上的唯一強解，并且證明了（u,η）的先驗估計與時間T一致無關，所以，根據解的延拓理論，對于任意的時間T∈［0,∞］，（u,η）也是問題（1）～（3）在Ω×［0,∞］上的唯一強解.因此，（u,η）是問題（1）～（3）的唯一整體強解，且滿足強解的空間（19）.證畢.

［1］BARANGER C，BOUDIN L，JABIN P E，et al.A modeling of biospray for the upper airways：CEMRACS 2004-mathematics and applications to biology and medicine［J］.ESAIM Proc，2005，14：41-47.

［2］BOUDIN L，DESVILLETTES L，MOTTE R.A modeling of compressible droplets in afluid［J］.Commun.Math.Sci，2003，1：657-669.

［3］WILLIAMS F A.Spray combustion and atomization［J］.Physics of Fluids，1958，1：541-555.

［4］AMSDEN A A，OROURKE P J，BUTLER T D.Kiva-2，a computer program forchemical reactive flows with sprays［R］.Tech. Rep，Los Alamos National Laboratory，1989.

［5］CARRILLO J A，GOUDON T.Stability and asymptotic analysis of a fluid-particle interaction model［J］.Commun.Partial Differ.Equ，2006，31：1349-1379.

［6］BALLEW J.Mathematical Topics in Fluid-Particle Interaction［D］.Maryland：University of Maryland，2014.

［7］FANG D Y，ZI R Z，ZHANG T.Global classical large solutions to a 1D fluid particle interaction model：The bubbling regime ［J］.J.Math.Phys，2012，53：033706.

［8］GALDI G P.An introduction to the mathematical theory of the Navier-Stokes equations.［M］.New York：Springer-Verlag，1994.

Global Strong Solutions for the 3D Navier-Stokes Equation Coupled with Smoluchowskie Equation

HUANG Bing-yuan
（School of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong，521041）

In this paper，I consider the initial boundary problem for Navier-Stokes equation coupled with Smoluchowskie equation in a bounded smooth domain Ω?R3.In view of the local strong solutions obtained by Ballew in，I establish some a priori estimates globally in time，and then prove the global solutions.

Navier-Stokes equation；Smoluchowski equation；strong solution；global existence

0 175.4

A

1007-6883（2016）03-0015-04

責任編輯朱本華

2016-01-16

廣東省教育廳青年創新人才類項目（項目編號：2015KQNCX095）；韓山師范學院重點課題（項目編號：LZ201403）.

黃丙遠（1983-），男，廣東湛江人，韓山師范學院數學與統計學院講師.