一類具有奇性p-Laplacian-Rayleigh方程的周期正解

陳仕洲

（韓山師范學院數學與統計學院，廣東潮州　521041）

一類具有奇性p-Laplacian-Rayleigh方程的周期正解

陳仕洲

（韓山師范學院數學與統計學院，廣東潮州521041）

利用重合度理論，研究一類具有奇性的p-Laplacian-Rayleigh方程，獲得其周期正解存在性新的充分條件，推廣和改進了已有文獻中的相關結論.

p-Laplacian-Rayleigh方程；周期正解；奇性；重合度理論

1　引言及引理

在動力系統研究中，具有奇性的微分方程周期正解的存在問題已受到人們極大的關注［1-10］，例如起源于電子學理論中的電子束Brillouin聚焦問題可轉化為研究微分方程

周期正解的存在性［1-2］.文［3］和［4］分別研究了微分方程

文［3］在下列條件（H1）-（H5）下證明了方程（2）存在一個正周期解：

（H1）存在常數0＜d1＜d2,s.t.如果x是方程（2）正的連續T周期解，且滿足

周期正解的存在問題，完善、改進和推廣了文［3］、［4］等的結果.文［6-7］分別研究了具有奇性的Rayleigh方程

周期正解的存在問題.本文將研究一類較廣泛的既含有奇點又含有時滯的p-Laplacian-Rayleigh方程

對于周期邊值問題

其中f*：［0, T］×R×R→R是Caratheodory函數.

引理1［8］（Manasevich-Mawhin）設是有界開集.若下列條件成立

（1）?λ∈（0,1）,邊值問題

在?Ω無解；

（2）方程

在?Ω?R無解.

（3）deg｛F,Ω?R,0｝≠0.

引理2［9］設

引理3［10］設x∈C1（R,R）,x（t+T）≡x（t）,且?ξ∈［0, T］,|x（ξ）|≤d，則

2　主要結論

定理1設條件

（A1）存在常數0＜d1＜d2使得：.則是 Lp-Caratheodory函數，即g1對第一變元是可測的，對第二變元是連續的，且

被滿足，則方程（7）存在一個正的T-周期解.

證明考慮（7）的同倫方程

我們斷定

由（10）-（12）得

由（A1），x（t1-σ）≤d2,x（t2-σ）≥d1.從而易知

由引理2得

由方程（10）兩邊同乘以x（t），并在區間［0, T］上積分即得

當p=2時，由（A5）知

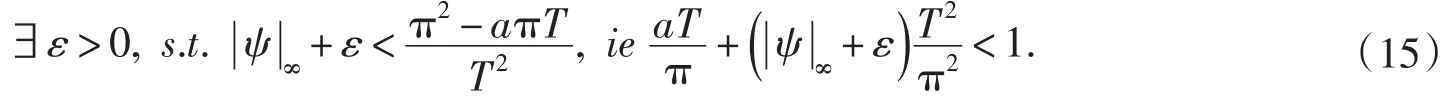
對此ε,?gε∈Lp（0,T）,s.t.（8）成立.注意到x（t）＞0,t∈［0, T］,有

由（14）和（16）得

由（A5）、（15）、（17）和（18）知，不論p=2還是

再由引理2得

由于x（0）=x（T），知?t0∈［0, T］,s.t.x'（t0）=0.于是

其中

將（10）積分可得

即

另一方面，由（10）得

上式兩邊同乘以x'（t）并注意到（A3）即得

設ξ∈［0,T］如同（13）中定義的.?t∈［ξ, T］，對（26）兩邊在［ξ,t］取積分得

由（27）-（32）得

由（A4）知，?M0＞0.s.t.x（t）≥M0.對于t∈［0, ξ］的情形，類似可證.

則Ω?X是有界開集.

顯然?λ∈（0, 1）,方程（10）在?Ω無解.

其次，?x∈?Ω?R,x（t）=q1（orq2），由（A1）有

（7）有一個正T-周期解x（t）.

注記1本文的結果是全新的.在方程（7）中，令p=2,σ=0,h=0,e=0，則為文［3］所研究的方程；令 p=2,h=0,e=0就是文［4］所研究的方程，易知定理1包含和推廣了文［4］的結果；令h=0,，則就是文［5］所研究的方程，可見本文定理1完善和發展了文［3-5］的結果；令p=2,f=0,e=0就是文［6］、［7］所研究的方程，易知本文定理1完善了文［6］的結果，包含和推廣了文［7］的結果.

［1］丁同仁.關于周期性Brillouin電子束聚焦系統的一個邊值問題［J］.北京大學學報，1965，1：31-38.

［2］葉彥謙，王現在.電子注聚焦理論中所出現的非線性微分方程［J］.應用數學學報，1978，1：13-41.

［3］ZHANG M.Periodic solutions of Liénard equations with singular forces of repulsive type［J］.J.Math.Anal.Appl.，1996，203：254-269.

［4］WANG Z.Periodic solutions of Liénard equation with a singularity and a deviating argument［J］.Nonlinear Analysis：Real World Applications，2014，16：227-234.

［5］陳仕洲.具有奇點和時滯的p-Laplacian方程的正周期解［J］.韓山師范學院學報，2015，36（3）：10-15.

［6］WANG Z，MA T.Periodic solutions of Rayleigh equations with singularities［J］.Boundary Value Problems，2015（1）：1-14.

［7］鐘濤，魯世平.具有奇性的時滯Rayleigh方程周期正解存在性［J］.鄭州大學學報：理學版，2015（2）：7-12.

［8］MAN′ASEVICH R,MAWHIN J.Periodic solutions for nonlinear systems with-Laplacian-like operators［J］.J.Differential Equations，1998，145（2）：367-393.

［9］LI J W，WANG G Q.Sharp inequalities for periodic functions［J］.Applied Mathematics E-Notes，2005（5）：75-83.

［10］張志戎，魯世平.一類具偏差變元高階p-Laplace微分方程的周期解［J］.吉林大學學報：理學版，2011，49（1）：71-75.

Positive Periodic Solutions for a Kind ofp-Laplacian-Rayleigh Equation with Singularity

CHEN Shi-zhou
（School of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong，521041）

By using the continuation theorem of coincidence degree，a kind of p-Laplacian-Rayleigh equation is studied with a singularity and a deviating argument.Some new sufficient conditions for the existence of positive periodic solutions are obtained.The results have extended and improved the related reports in the literatures.

p-Laplacian-Rayleigh equation；positive periodic solution；singularity；coincidence degree；

O 175.12

A

1007-6883（2016）03-0008-07

責任編輯朱本華

2016-04-06

廣東省高等教育教學改革項目（項目編號：GDJG20142396）；韓山師范學院理科團隊項目（項目編號：LT201202）.

陳仕洲（1959-），男，廣東汕頭人，韓山師范學院數學與統計學院副教授.