偶階中立型多時滯泛函微分不等式最終正解的不存在性
林文賢
(韓山師范學院數學與統計學院,廣東潮州 521041)
偶階中立型多時滯泛函微分不等式最終正解的不存在性
林文賢
(韓山師范學院數學與統計學院,廣東潮州521041)
利用廣義黎卡提變換和積分平均技巧,研究了一類非線性的偶數階中立型多時滯泛函微分不等式,得到了該類不等式幾個新的最終正解不存在準則,所得結果推廣了最近文獻的相關結果,具有重要意義.
中立型;多時滯;泛函微分不等式;最終正解
1 引言
振動是系統的主要動力學性質之一,在日常生產、生活中,振動現象屢見不鮮,如機械振動、聲帶振動、電磁振蕩等.由于振動的復雜性,人們往往通過簡化假設,建立相應的數學模型,把復雜的振動問題用相對簡單的數學方法加以描述,這便是動力方程的振動理論.動力方程的振動理論是微分方程定性理論的一個重要分支,在控制工程、機械振動、生物制藥、力學等領域具有重要的應用價值.
1836年,Sturm在研究熱傳導問題時首次研究了二階動力方程的振動性.此后,一個多世紀內,微分方程的振動理論發展比較緩慢,直到20世紀七八十年代,微分方程的振動理論逐漸成為了國內外學者研究的熱點;隨著研究的深入,研究的對象由線性微分方程拓展到次線性方程、半線性方程、超線性方程等情形,方程的階數由二階拓展到三階,再拓展到偶數階,由連續動力拓展到離散動力方程、時間尺度上的動力方程,而且研究的方程也由一般情形拓展到時滯方程、中立型方程、阻尼方程等情形.
近年來,中立型泛函微分不等式和微分方程出現了許多研究成果,參見文獻[1-26].本文將考慮如下一般形式的非線性偶數階中立型多時滯不等式
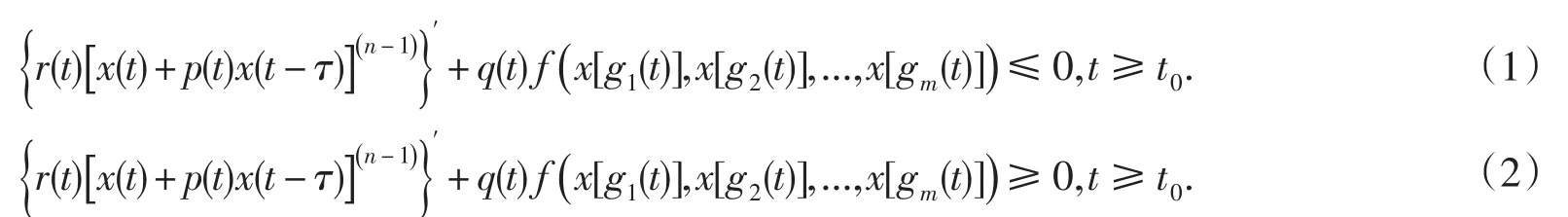
其中n是偶數,τ>0為常數.給出不等式(1)和(2)幾個新的最終正解不存在準則.
關于不等式(1),本文始終假設下列條件成立:
i∈Im={1,2,...,m};
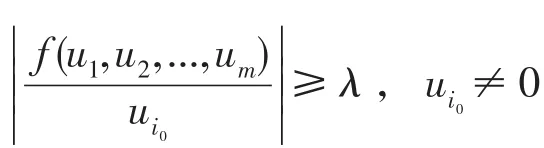
為得到本文的結果,首先給出如下引理.
引理1[27]設不恒為零,則和整數為奇數,使對t≥tu有u(k)(t)>0,0≤k≤l且(-1)k+1u(k)(t)>0,l≤k≤n.
引理2[28]設引理1的條件成立,且u(n-1)(t)?u(n)(t)≤0,t≥t0,則?θ∈(0, 1)和M>0,使得對充分大的t有
2 主要結果
定理1 假設條件(Η1)~(Η4)成立,對任意整數m>2,若θ∈(0, 1)和M>0,使得
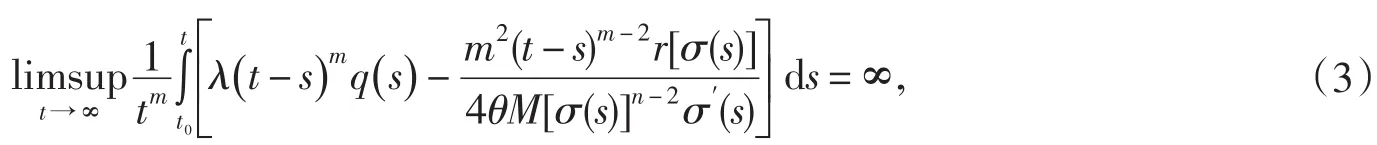
則不等式(1)無最終正解.
證明假設相反,x(t)是(1)的最終正解則?t1≥t0,使得x(t)>0,x(t-τ)>0,x[gi(t)]>0,t≥t1,再由(Η2)得令

則有y(t)≥x(t)>0,[r(t)y(n-1)(t)]′≤0,t≥t1.
于是由(Η1)可得,y(n)(t)≤0,y(n-1)(t)>0,t≥t2.又由引理1,?t2≥t1,使得y′(t)>0,t≥t2.令

則z(t)≥0.由于x(t)≤y(t),因此x[gi(t)]≤y[gi(t)](i∈Im).注意到y′(t)>0及條件(Η3)(Η4),有
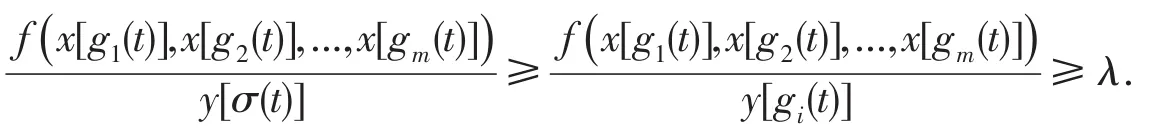
這樣
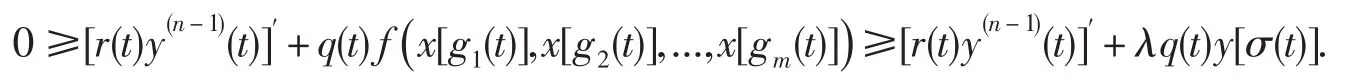
于是對于常數θ∈(0, 1),有
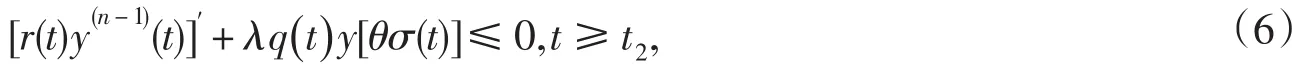
注意到y(n-1)[σ(t)]>0,y(n)[σ(t)]≤0,t≥t2,于是有引理2,有
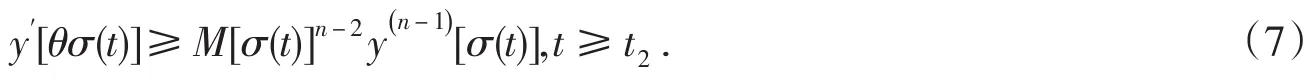
這樣,由(5)、(6)及(7)得
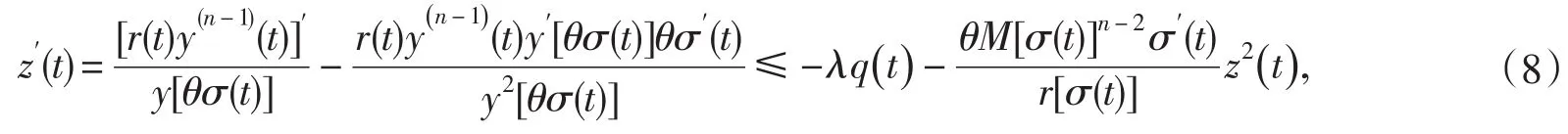
由此可得,對于任意的t≥t2,有
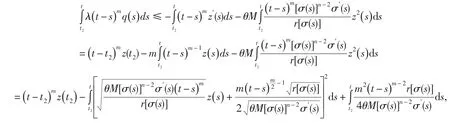
進一步,有
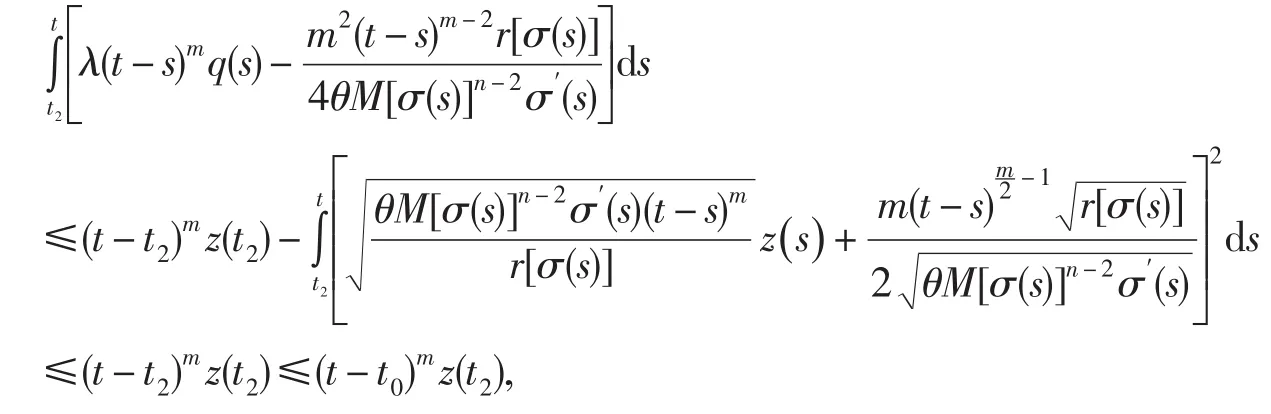
于是,有
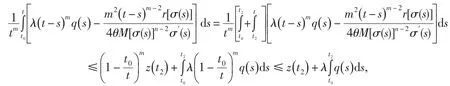
對上式令t→∞,并取上極限得
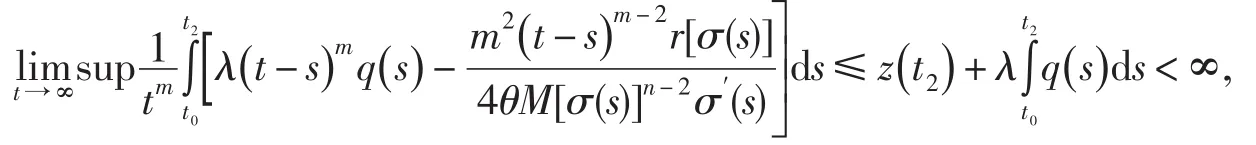
此與公式(3)矛盾.定理1證畢.
推論1若定理1中的(3)式被替代為
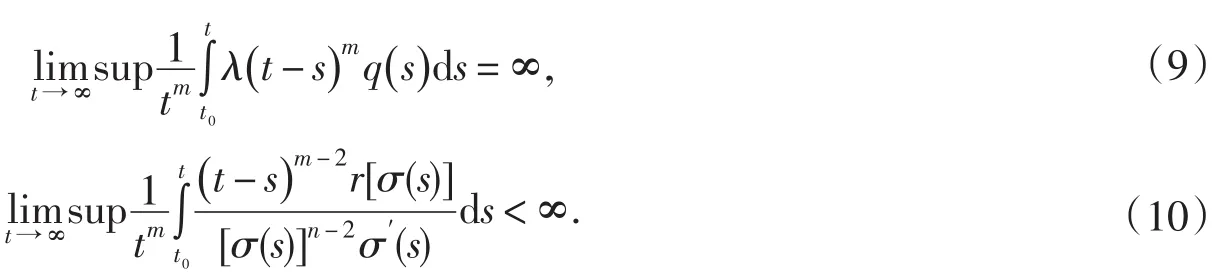
則不等式(1)無最終正解.
定理2 假設條件(Η1)~(Η4)成立,如果存在常數m≥2和函數,使得
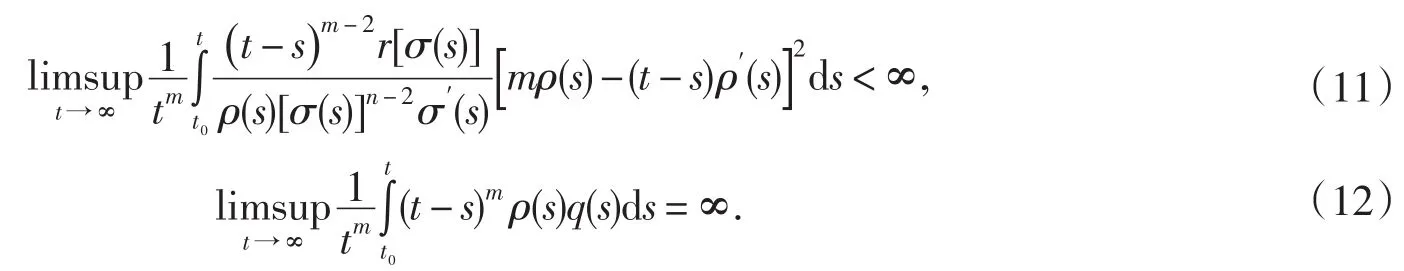
則不等式(1)無最終正解.
證明假設相反,x(t)是(1)的最終正解,則由定理1的證明知,?t2≥t1≥t0,θ∈(0, 1)和M>0
使得(8)式成立,這樣
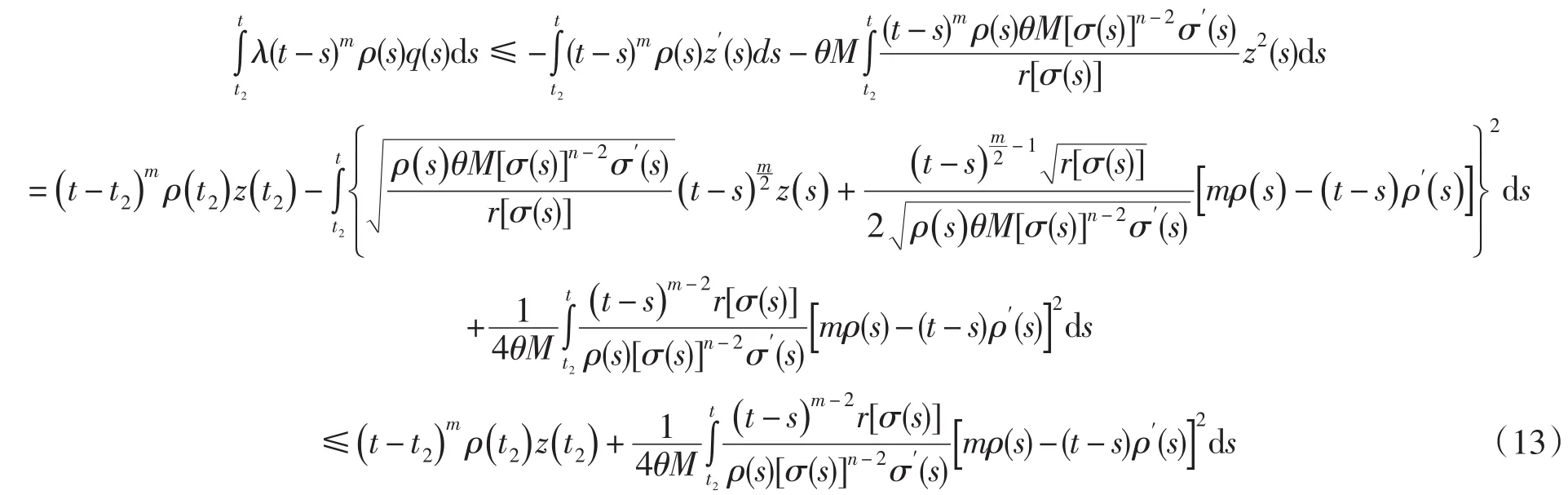
進一步,有
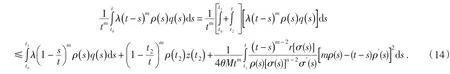
令t→∞,并取上極限得
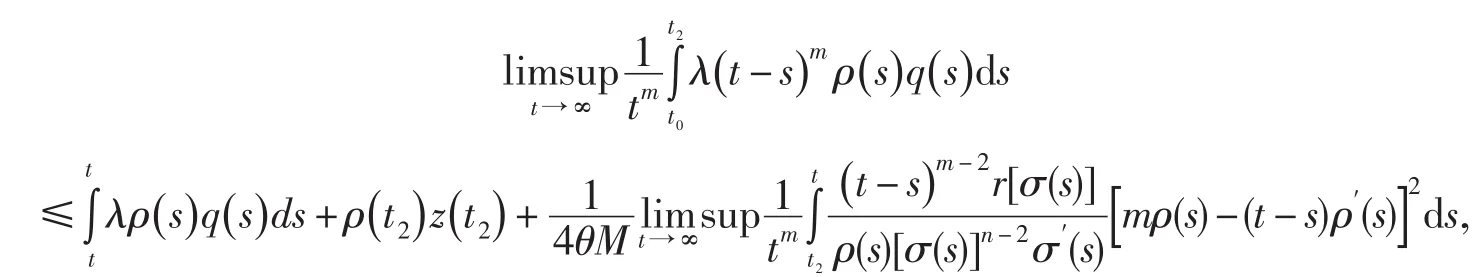
由公式(11),有
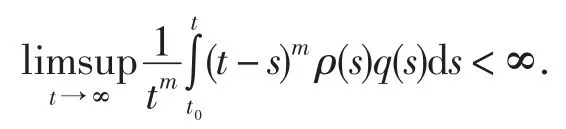
此與公式(12)矛盾.定理2證畢.
定理3 假設條件(Η1)~(Η4)成立,如果存在常數m≥2和函數,使得
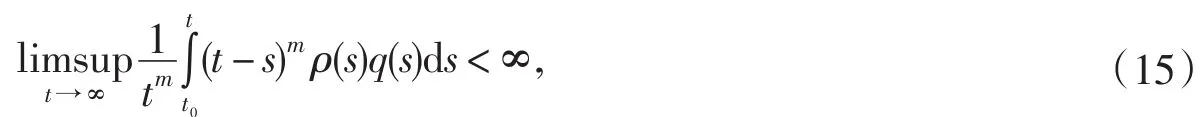

則不等式(1)無最終正解.
證明假設相反,x(t)是(1)的最終正解,則由定理2的證明知?t2≥t1≥t0,存在常數θ∈(0, 1)和M>0,使得當t>u≥t2時有(13)成立.進一步,有
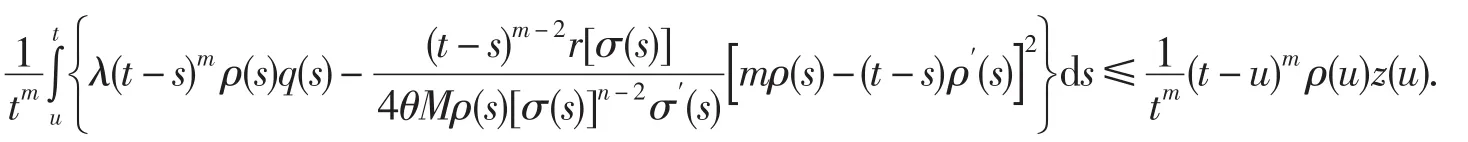
令t→∞,并取上極限,并注意到(16)可得φ(u)≤ρ(u)z(u),u≥t2.因此

定義函數
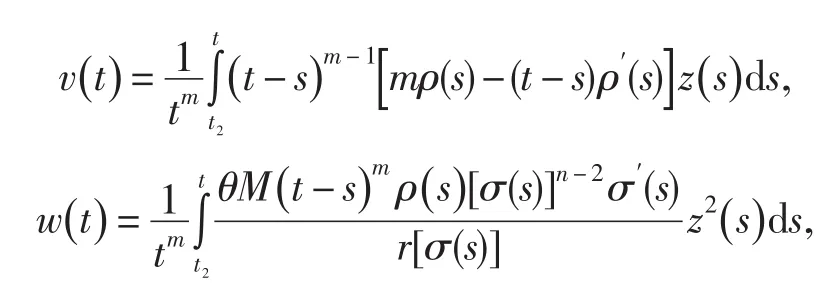
則由(13)可知
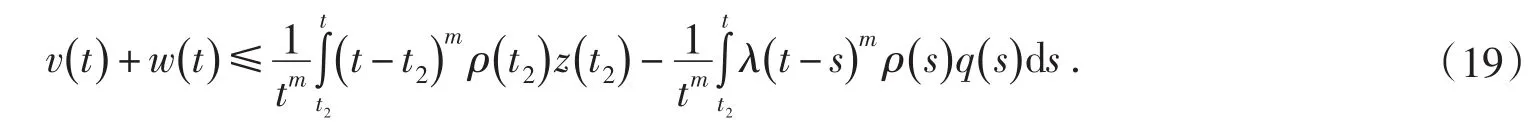
注意到(16)式,有
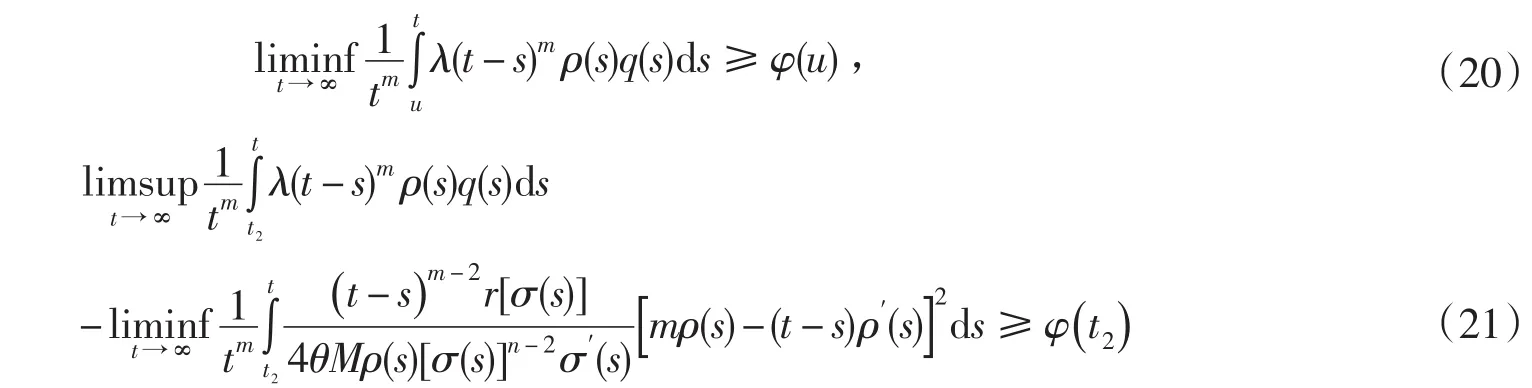
由(15)和(21)得
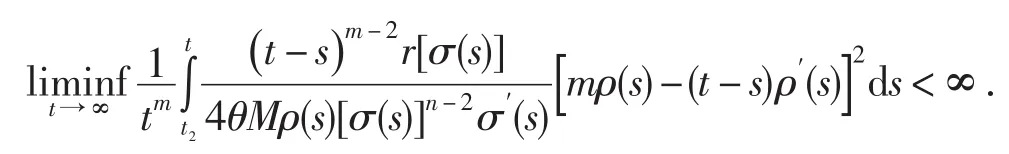
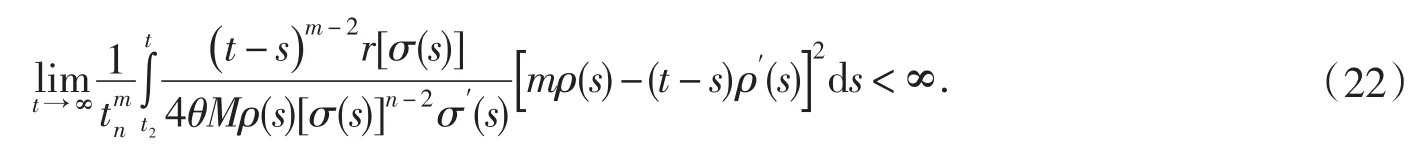
在(19)中令t→∞,取上極限,并使用(20)式可得
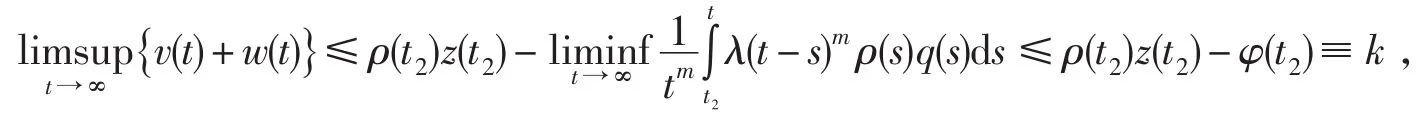
因此對充分大的n,有

其中k1>k為常數,從w(t)的定義有
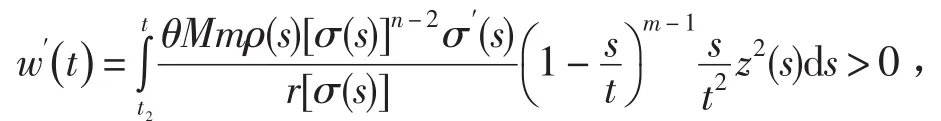

因此,對任意的0<∈<1,當n充分大時

另一方面,由Schwarz不等式得
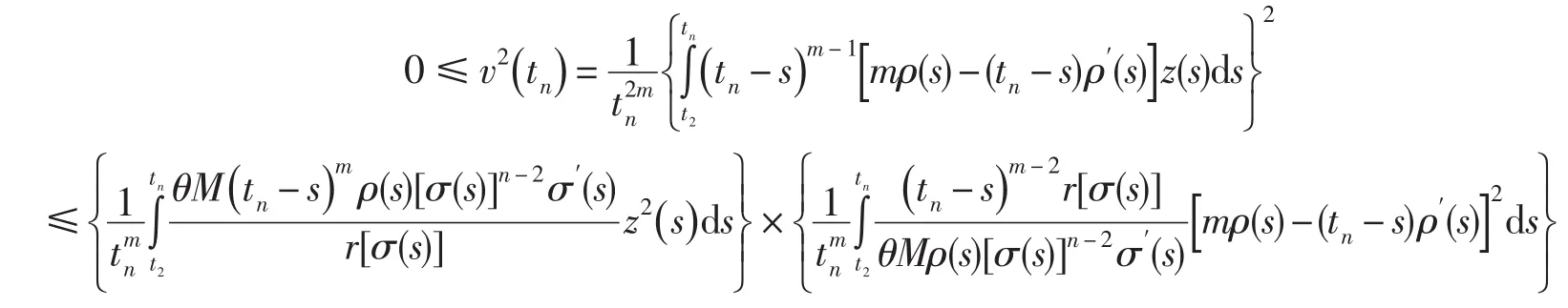
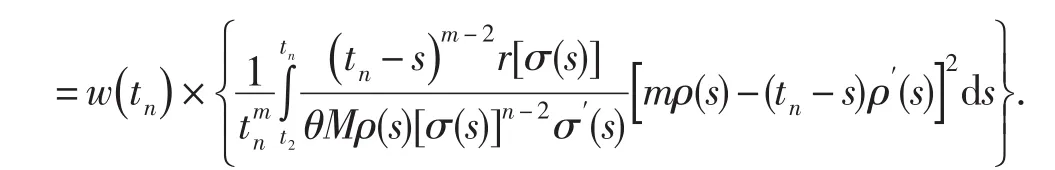
因此
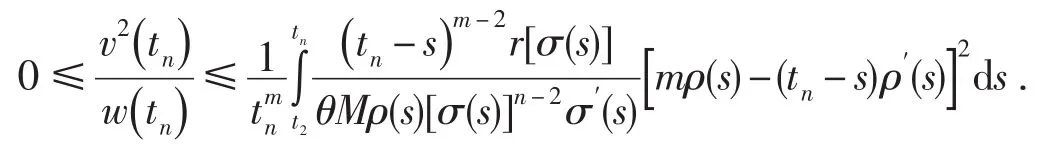
令t→∞,并注意到(22)式,得

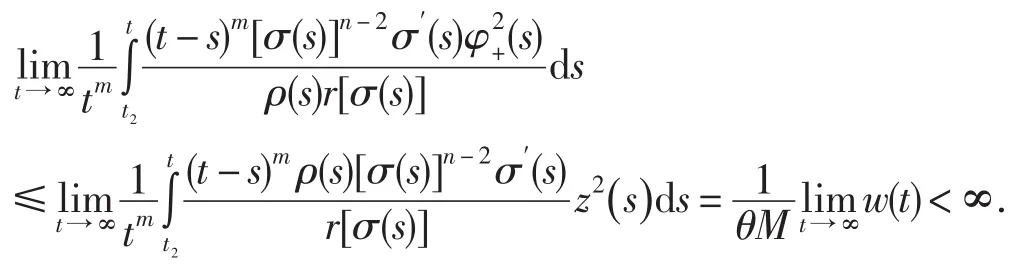
進一步有
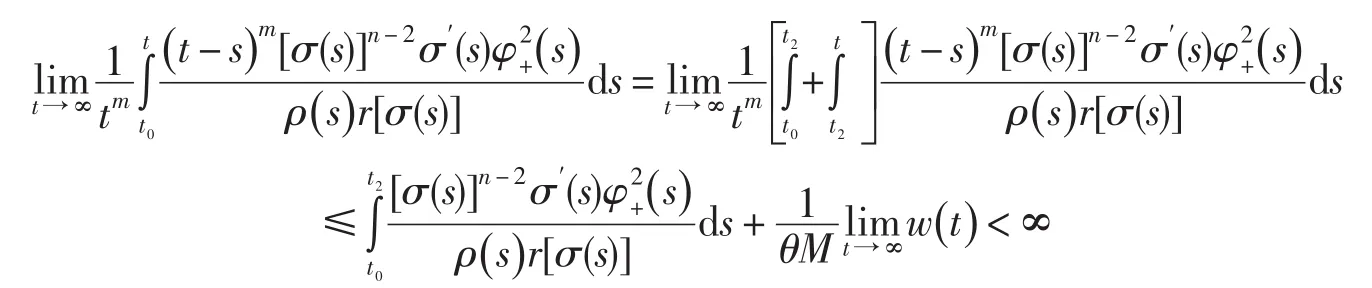
此與公式(17)矛盾.定理3證畢.
類似于不等式(1),也得到不等式(2)的一些結果.
定理4假設定理1條件成立,則不等式(2)無最終負解.
定理5假設定理2條件成立,則不等式(2)無最終負解.
定理6假設定理3條件成立,則不等式(2)無最終負解.
注:當r(t)≡1時,不等式(1)就是文獻[4]所研究的不等式,因而本文的結論推廣和包含了文獻[4]的結果.
[1]RUAN J.A class of differential inequalities with continuous distributed deviating arguments[J].Acta Math Sinaca,1987,30:661-670.
[2]WANG P G,GE W G.Certain of second differential inequalities of neutral typed[J].Appl.Math.Letters,2000,13(1):45-51.
[3]LIN Wenxian.A note on oscillation for systems of high order quasilinear partial differential eqations of neutral type[J].Applied Mathematics and Computation,2004,156(3):563-576.
[4]林丹玲,俞元洪.偶階中立型泛函微分不等式最終正解的不存在性[J].數學的實踐與認識,2009,39(15):235-241.
[5]林文賢.具連續分布滯量的二階中立型方程的振動性定理[J].應用泛函分析學報,2003,5(2):174-177.
[6]林文賢.一類非線性偶數階中立型方程的振動準則[J].工程數學學報,2005,22(1):159-162.
[7]林文賢.一類中立型泛函微分方程的振動準則[J].數學的實踐與認識,2005,35(6),211-215.
[8]林文賢.一類具連續分布滯量的偶數階微分方程的新振動性定理[J].遼寧師范大學學報:自然科學版,2006,29 (4),394-396.
[9]林文賢.一類具連續偏差變元的二階非線性中立型方程的振動性[J].西南師范大學學報:自然科學版,2009,34 (4):1-3.
[10]LIN Wenxian.Interval oscillation theorems for certain second order neutral differential equations with continuous deviating arguments[J].Southeast Asian Bulletin of Mathematics,2010,34(6):1055-1061.
[11]林文賢.具有阻尼項的中立型Emden-Fowler方程的區間振動準則[J].韓山師范學院學報,2011,32(6):8-11.
[12]LIN Wenxian.A note on oscillation of certain second order partial functional differential equation with damping[J].Pioneer Journal of Mathematics and Mathematics Sciences,2012,4(1):125-128.
[13]林文賢.具連續分布時滯的二階半線性中立型阻尼泛函微分方程的Philos型振動定理[J].韓山師范學院學報,2012,33(3):7-12.
[14]林文賢.一類二階中立型微分不等式最終正解的不存在性[J].河南師范大學學報:自然科學版,2012,40(2):31-33.
[15]林文賢.二階中立型阻尼微分不等式最終正解不存在性[J].蘭州理工大學學報,2012,38(5):138-140.
[16]林文賢.具連續偏差變元的二階阻尼微分方程的振動性[J].中國科學院研究生院學報,2012,29(5):594-598.
[17]林文賢.一類具阻尼項和連續分布滯量的偶數階中立型方程的振動性[J].西南師范大學學報:自然科學版,2012,37(9):1-3.
[18]LIN Wenxian.Oscillation theorems for certain higher order neutral equations with continuous distributed deviating arguments[J].Southeast Asian Bulletin of Mathematics,2012,34(4):849-854.
[19]林文賢.一類中立型阻尼泛函微分方程的振動性[J].四川師范大學學報:自然科學版,2013,36(3):20-22.
[20]林文賢.一類偶階中立型分布時滯不等式最終正解的不存在性[J].韓山師范學院學報,2013,34(3):6-12.
[21]林文賢.一類三階中立型阻尼方程的Philos型振動定理[J].寧夏大學學報:自然科學版,2014,35(2):1-4.
[
22]林文賢.一類帶強迫項的二階阻尼微分方程的區間振動性[J].鄭州大學學報:理科版,2014,46(2):1-5.
[23]林文賢,俞元洪.高階中立型時滯微分方程的振動準則[J].應用數學學報,2014,37(6):1018-1024.
[24]林文賢.振動性和周期解理論的研究[M].北京:國防工業出版社,2014.
[25]林文賢,陳秋杏.具阻尼項的偶階中立型微分不等式最終正解的不存在性[J].瓊州學院學報,2014,21(5):6-11.
[26]林文賢.具分布式偏差變元和阻尼項的中立型雙曲方程的振動性[J].西南師范大學學報:自然科學版,2015,39 (1):1-4.
[27]KIGURADZE I T.On the oscillation of solutions of the equationMat Sb,1964,65: 172-187.
[28]PHILOS Ch G.A new criterion for the oscillatory and asymptotic behavior of delay differential equations[J].Bull Acad Pol Sci Ser Sci Mat,1981,39:61-64.
The Nonexistence for Eventually Positive Solutions of Even Order Neutral Functional Differential Inequality with Multiple Delays
LIN Wen-xian
(School of Mathematics and Statistics,Hanshan Normal University,Chaozhou,Guangdong,521041)
Using a generalized Riccati transformation and integral averaging technique,we develop several new results related to the nonexistence criteria for eventually positive solutions of certain even order neutral functional differential inequalities with multiple delays.The results extend and improve the ones in recent literature,and have important significance.
neutral;multiple delays;functional differential inequalities;eventually positive solutions
O 175.27
A
1007-6883(2016)03-0001-07
責任編輯朱本華
2016-03-08
廣東省高等教育教學改革項目(項目編號:GDJG20142396);廣東省高等學校特色創新項目(項目編號:2014GXJK125).
林文賢(1966-),男,廣東潮州人,韓山師范學院數學與統計學院教授.

