一種采用LC耦合的電氣化鐵道功率調節(jié)系統(tǒng)

胡斯佳 張志文 李 勇 羅隆福 羅 培

（湖南大學電氣與信息工程學院 長沙 410082）

一種采用LC耦合的電氣化鐵道功率調節(jié)系統(tǒng)

胡斯佳 張志文 李 勇 羅隆福 羅 培

（湖南大學電氣與信息工程學院 長沙 410082）

針對電氣化鐵道異相供電系統(tǒng)中牽引網過分相及電能質量問題，采用鐵路功率調節(jié)器（RPC）的單相供電方式是一種可行方案。然而，RPC較大的補償容量使得該套系統(tǒng)有源部分成本高。為提高該方案的性價比和可靠性，提出一種適用于單相牽引供電系統(tǒng)的 LC耦合型鐵路功率調節(jié)器（LC-RPC）。在對LC-RPC端口特性進行分析的基礎上，提出一種適用于電氣化鐵道隨機波動負荷條件下LC耦合支路電抗的最小運行電壓設計。與傳統(tǒng)RPC系統(tǒng)進行了詳細容量對比分析，結果表明LC-RPC具有顯著節(jié)容優(yōu)勢。結合某牽引變電所的實測數(shù)據(jù)給出了系統(tǒng)的參數(shù)設計實例。最后，仿真和實驗結果驗證了LC-RPC補償效果和節(jié)容能力的有效性。

LC耦合 鐵路功率調節(jié)器 參數(shù)設計 容量分析 電能質量

0 引言

隨著我國鐵路運輸中高速、重載列車所占比例不斷增加，經牽引變電所滲透至三相公共電網的負序、諧波和無功也日益增多，對既有供電系統(tǒng)的安全和穩(wěn)定運行構成了嚴峻挑戰(zhàn)，引起了相關工業(yè)部門和學者的廣泛關注[1,2]。

考慮到經濟性，我國牽引變電所高壓進線普遍采用相序輪換技術。但對于山區(qū)、高原等電網相對薄弱地區(qū)的牽引變電所，該方法難以達到國家標準對電壓不平衡度的要求[3]。采用平衡牽引變壓器能獲得比非平衡牽引變壓器更強的負序抑制能力，但該能力受機車負荷的波動影響較大，負荷越不平衡，平衡變抑制負序的能力越差[4,5]。在牽引變電所采用SVC，能對兩相牽引供電系統(tǒng)的負序和無功進行綜合補償，但在技術和經濟上很難同時達到理想狀態(tài)[6]。

針對上述方法的不足，學者及工程師們提出了多種基于IGBT或IGCT等全控型功率器件的有源拓撲結構[7-15]及SVC多站協(xié)同補償方法[16]。在眾多方案中，鐵路功率調節(jié)器（Railway static Power Conditioner，RPC）以其較好的通用性受到了廣泛關注[11-15]。RPC通過重新分配牽引變壓器出口處有功潮流，并獨立補償各相的無功和諧波，能有效解決兩相[14]或單相[15]牽引供電系統(tǒng)的主要電能質量問題。但較高的容量和投資成本限制了RPC的大規(guī)模推廣應用，現(xiàn)僅在日本的少數(shù)牽引變電所投入了實際應用[13-15]。

此外，具有較高性價比的混合電力調節(jié)系統(tǒng)的研究主要集中在以動態(tài)諧波補償為主要目標的有源電力濾波器上[17-20]；對于電氣化鐵路隨機波動負荷條件下，以負序、無功和諧波綜合補償為目的的混合型RPC的研究仍然很少[12]。為提高常規(guī)RPC的性價比、補償效果和可靠性，本文提出一種采用 LC耦合的鐵路功率調節(jié)器（LC-coupled RPC，LC-RPC）。LC-RPC基于兩臺單相變壓器，因其變流器與主變壓器的耦合部分采用基波下呈容性的LC串聯(lián)電路而得名（RPC采用電感支路）。LC-RPC 較RPC在容量、補償能力及可靠性上更具優(yōu)勢，故其性價比更高。本文將對LC-RPC的運行特性進行理論分析，提出隨機波動負荷條件下關鍵器件的設計原理，并討論系統(tǒng)的容量特性，最后，通過仿真與實驗驗證了該系統(tǒng)的優(yōu)越補償效果與節(jié)容能力。

1 LC-RPC的拓撲結構

圖1為LC-RPC的拓撲結構。主牽引變壓器由Tα、Tβ按V/v變壓器聯(lián)結。其中，Tα將來自電網的高壓電降至 27.5kV供機車使用。Uβ一般不等于27.5kV，其數(shù)值應根據(jù)LC耦合電抗Xα、Xβ及負載統(tǒng)計結果綜合考慮。該系統(tǒng)的有源部分由兩單相電壓源型變流器背靠背連接組成，其中 conα 經 Xα與Tα的低壓繞組及牽引網相連，conβ 經 Xβ與 Tβ的低壓繞組相連。在工程中，conα、conβ 宜采用多電平拓撲結構，可省去兩個大容量工頻降壓變壓器，經濟性較好[7,8]。

LC-RPC的兩相等效電路如圖 2所示。其中，Uck、Ick分別為變流器 k的端口基波電壓和電流，k=α,β；Xk、UXk分別為 k相耦合支路的電抗和基波壓降；Uk、Ik分別為Tk低壓側的端口電壓、電流；IL為負載電流。

圖1　LC-RPC的拓撲結構Fig.1 Topology of LC-RPC

圖2　LC-RPC的兩相等效電路Fig.2 Two-phase equivalent circuit of LC-RPC

2 LC-RPC的端口特性

2.1變流器基本特性要求

暫不考慮 Tα、Tβ電壓比不同的影響，LC-RPC的相量圖如圖3所示。

圖3　補償原理相量圖Fig.3 Phasor diagram of compensation principle

本系統(tǒng)的核心在于將負載電流IL有功分量的一半從 β相（DO）轉移至α相（GF）（此時 conβ為整流器、conα 為逆變器，負載的功率由 Tα、Tβ共同分擔），并對α相補償適當容性無功（長度為BC），對β相補償適當感性無功（長度為DE）。最終將Tα、Tβ的輸出電流分別從IL和0校正為Iα*和Iβ*。故主變一次電流將轉變?yōu)镮A*、IB*和IC*，顯然它們三相對稱且功率因數(shù)為1。因此，conα和conβ需要補償?shù)幕娏鞣謩e為Icα和Icβ。

根據(jù)圖3，角度δα（Uα與Icα的夾角）與負載功率因數(shù)λ（λ=cosθα）應滿足

式中，Icαp、Icαq分別為Icα的有功分量和無功分量，對應圖3中的AB和BC。δα與λ的關系如圖4所示，δα隨λ的增加單調減小。

圖4　δα-λ 曲線Fig.4 Curve of δα-λ

conα 補償電流Icα與負載電流IL滿足

式中

2.2變流器端口電壓

由圖2a，α相變流器端口電壓Ucα可表示為

式中，Uα為α側負載端口電壓有效值；Xα為α側 LC耦合支路基波等值電抗，Xα=ωLα1/?(ωCα)， ω 為基波角頻率；Icα為α側變流器補償電流有效值；δα為α 側Uα與Icα的夾角；f (*)代表多元函數(shù)。

本節(jié)將分兩種簡單情形分別討論 Ucα與 Icα和δα的關系，而關于它們之間更復雜的關系及Xα的設計將在第3節(jié)中討論。

假設條件：①Uα不變；②α相LC支路對基波呈容性。

2.2.1情形 1：Icα的相位一定（即δα一定），大小變化

此時，Ucα的末端在Icα的垂線L1上變動，相量關系如圖5所示。圖5說明，當Icα由小變大時（Icα1→Icα→Icα2），Ucα經歷了由大變小，再由小變大的過程（Ucα1→Ucαm→Ucα2）。

圖5　δα一定時，Ucα的變化情況Fig.5 The change of Ucαwhen δαis constant

Ucα的最小值 Ucαm出現(xiàn)在 Ucα與 Icα重合的位置（圖中D點）。對每一個δα角度，均存在Ucα的最小值Ucαm，且滿足

式中，|Xαm|對應 Ucα=Ucαm時，α相 LC耦合支路基波等值容抗的絕對值。

2.2.2情形2：Icα的大小一定（Icα=Icαm=I′cα），但相位變化

此時，Ucα與δα和Xα均有關。又假定Xα一定（容性），相量關系如圖6所示。圖6中各變量具有下列關系

圖6　Icα的大小一定時，Ucα的變化情況Fig.6 The change of Ucαwhen Icαis constant

圖 6說明，當 Xα一定，Icα大小不變，但 Icα與Uα的夾角變化時，對應的變流器輸出電壓不相同，即conα 的補償電流與Uα的夾角越小（見圖中δα），變流器輸出電壓越大（見圖中 Ucα）。由于δα隨λ 的增加單調下降，圖6的結論也可表述為：在Xα及Icα的大小一定時，負載的功率因數(shù)越高，conα 的輸出電壓越大，逆變器的視在功率也越大（圖中 UcαIcα＞UcαmIcαm＞U′cαI′cα）。

3 參數(shù)設計及控制

3.1α 相LC耦合支路設計

3.1.1Xα與變流器的協(xié)同設計原則

如上所述，Xα的大小與變流器的性能以及輸出電壓和電流直接相關，是一個非常重要的設計變量。

考慮到電氣化鐵路的負荷具有隨機波動和沖擊的特點，其在不同的時間段具有不同的負荷。同時，負荷的功率因數(shù)也在一定范圍內隨機波動。設計參數(shù)時如何既考慮系統(tǒng)安全、可靠性又兼顧經濟性，這是本文關注的重點。

為此，提出Xα與conα的協(xié)同設計原則如下：

（1）選取的Xα應使得變流器在重載最大補償電流時的輸出電壓最低。這樣，可以降低逆變器輸出的視在功率，減少成本和運行損耗[21]。更重要的是，重載時牽引網對公共電力系統(tǒng)的影響最大，而且是變流器故障頻發(fā)的薄弱環(huán)節(jié)[22]，該原則有利于提高系統(tǒng)的補償能力和可靠性。

（2）在滿足設計原則（1）的前提下，選取的Xα應使得變流器能夠輸出的視在功率盡可能高。這樣，變流器的容量利用率較大。

（3）選取的Xα應使得負荷在典型動態(tài)變化范圍內，設計出的變流器較傳統(tǒng)RPC具有明顯經濟優(yōu)勢。

3.1.2Xα的設計思想

1）設計原則（1）的驗證

首先在圖 7中給出α相變流器的端口電壓和電流相量。由圖可知四個補償電流 Icα、I′cα、IcαM和

I′cαM滿足 Icα=I′cα＜IcαM=I′cαM；且滯后 Uα的角度分別為δα、δαm、δαm和δ′αm。此處定義δαm為補償電流相角的最小值，IcαM為補償電流相量幅值的最大值。考慮到δα＜90°（見圖 4），所以補償電流相量將位于圖7所示陰影扇形區(qū)域及其邊界上。由于上述四種補償電流相量分別代表了該區(qū)域的邊界和一般情況，故在LC-RPC中對它們進行分析具有普遍意義。另外，與 Icα、I′cα、IcαM和 I′cαM對應的 conα 的電壓三角形分別為△ABO、△ACO、△ADO和△AEO。

由于δα隨λ 的增加而遞減（見圖4），所以在圖7中與 I′cα、IcαM對應的負載的功率因數(shù)最高，I′cαM次之，Icα最低。由于I′cα＜IcαM，所以IcαM為與最大負載功率因數(shù)對應的最大補償電流的相量。

圖7　α相的電壓、電流相量圖Fig.7 Voltage and current phasor diagram of phase α

在設計時，為確保系統(tǒng)安全可靠，應取重載時變流器的最大補償電流作為額定電流，故圖 7中IcαM=I′cαM為conα的額定電流。為滿足設計原則（1），設計的 Xα應使得變流器在額定電流時的輸出電壓最低，以該最小電壓作為變流器的額定電壓，這樣，變流器額定視在功率最低。受圖5啟發(fā)可知，在圖7中 OD、OF分別為與 IcαM、I′cαM對應的變流器的最小端口電壓，因此△ADO、△AFO可作為設計Xα的備選電壓三角形。若按與IcαM對應的△ADO確定Xα，則當補償電流為I′cαM時，變流器的端口電壓為OE，且＜OD。說明當額定補償電流相量發(fā)生變化時（相量終點在弧線LH上移動），若采用△ADO確定Xα，變流器的端口電壓將不會超過OD。但若按與I′cαM相對應的△AFO確定Xα，當額定補償電流變?yōu)镮cαM時，變流器的端口輸出電壓為OG，顯然OG ＞OD，Xα表現(xiàn)為過補償，其所提供的補償電壓AG過高，此時變流器的輸出電壓和視在功率也過高，反而不利于變流器工作。綜上所述，在額定電流條件下宜按△ADO確定 Xα，這樣，變流器的額定視在功率最低。所以，Xα的最優(yōu)容抗絕對值|Xα-opt|可由△ADO確定為

式中，IcαM為補償電流的最大有效值；δαm為補償電流相量與Uα夾角的最小值，且滿足（參照式（1））

式中，λmax為負載的最大功率因數(shù)。

2）設計原則（2）的驗證

按式（7）設計出Xα-opt之后，需要研究負荷和功率因數(shù)變化時，變流器輸出的視在功率。對于同一牽引供電系統(tǒng)，由圖7可知，當補償電流從額定電流 IcαM減小為 I′cα時，△ADO將退化成△ACO，此時 conα的端口電壓將由 Ucαopt增大為 Ucα，所以在額定電流下采用△ADO所得到的|Xα-opt|不一定能確保系統(tǒng)在負荷變化時conα的端口視在功率最大；另外，對于不同的牽引供電系統(tǒng)，由于其承擔的運輸任務及機車類型不盡相同，其λmax也可能不同，故式（7）是否滿足設計原則（2）需通過驗證。這將是下文討論的主要內容。

由2.2.2節(jié)情形2的結論可知，在圖7中，與△AEO相比，△ADO所對應的conα 的視在功率較大；同理，△ABO和△ACO中，后者所對應的變流器視在功率較大。這說明如需使conα的視在功率達到最大值，△ABO中（一般工況下的電壓三角形），Ucα的終點 B必須始終限制在 AD上移動。此時△ABO→△ACO，Icα→I′cα。由△ACO可得與其對應的conα 的視在功率Scα為

式中，I′cα已被Icα代替，因為此時△ABO≌△ACO。考慮到式（7）和式（8），并將式（9）轉化成標幺值后，可得圖8，其中基準值為UB=Uα、IB=IcαM。

由圖8可知，當λmax為0.7～1.0區(qū)間（電力機車功率因數(shù)的典型變化區(qū)間）的某一值時，Scα的最大值恰好出現(xiàn)在Icα=1.0(pu)處（對應圖8中AB上的某點）。說明對于牽引負荷來說，采用式（7）設計的 Xα，確實在 Icα=IcαM及δα=δαm（或者λ=λmax）時具有最大視在功率（即變流器的額定視在功率）。故采用△ADO設計的|Xα-opt|滿足設計原則（2）。

設計原則（3）的驗證將在第4節(jié)中討論。

當 Icα=IcαM時，變流器的端口運行電壓Ucα達到該條件下的最小值Ucαopt，故此，本文將上述設計方法命名為 LC-RPC中 Xα的最小運行電壓設計法（Minimum Operating Voltage Design Method, MOVDM）。

圖8　Scα與Icα和λmax的關系Fig.8 The relationship of Scα, Icαand λmax

3.1.3Xα的工程設計

由于Icα不利于測量，故由式（7）所確定的|Xα-opt|難以直接計算，本節(jié)將給出以易于測量的負載電流IL作為變量的|Xα-opt|的工程計算方法。

由式（3）可得到如圖9所示的ε 關于λ 的函數(shù)曲線。由圖9可知，當λ∈[0.7, 0.9]時，ε 的變化范圍較小。由于機車負荷的功率因數(shù)出現(xiàn)在 0.7～0.9區(qū)間的概率較其他值高，所以可近似認為 Icα與 IL成正比。參考式（2）和式（3）可認為

式中，ILM為負載電流的最大有效值；εav為當λ∈[0.7, 0.9]時ε 的平均值。

圖9　ε (λ)和ξ1(λmax)曲線Fig.9 Curves of ε (λ) and ξ1(λmax)

將式（10）和式（8）代入式（7）可得|Xα-opt|的工程計算表達式為

式中

為方便設計將ξ1(λmax)繪制于圖9中虛線部分。

另外，由于在工程中一般采用95%概率值進行計算，故式（11）也可進一步改寫為

式中，95%λ（上）、L95%I（上）分別為λ和IL的上限95%概率值。若考慮濾波，在滿足式（11）或式（13）的前提下，Lα和Cα還可對第n次（一般n=5或7[20]）諧波全調諧設計。

3.2β 相LC耦合支路設計

β相的相量如圖10所示（見圖2b）。其中，IcβM為 conβ 的最大補償電流、與 Uα垂直（其方向與圖3中Icβ相同），Uβ滯后Uα60°，UcβM為conβ的最大端口電壓相量。

圖10　β相的電壓、電流相量Fig.10 Votage and current phasor diagram of phase β

本文設計β相參數(shù)的原則是：①當 conα發(fā)出最大補償電流IcαM時，應使UcβM=Ucαopt，這樣在補償系統(tǒng)負擔最重時，兩個變流器的運行基本對稱。②β相參數(shù)應該在避免大電感的前提下具有較好的設計靈活性，這樣便于器件的選型及對原有設備的改造利用，有利于降低設計和采購成本。

故此處選擇 LC串聯(lián)且呈容性的支路作為β相的耦合支路。conβ典型的電壓三角形為圖 10中的△BEO，且滿足

式中，EB為LC耦合支路上的電壓降（滯后IcβM90°）；為β相LC耦合支路基波容抗的絕對值。另外，需要注意的是應設計Uβ＜Ucαopt。

考慮到當 Icβ=IcβM時，負載電流 IL的有功分量一定為最大值，故由圖3所示的α、β相補償電流的相量關系并計及變壓器的電壓比可得

式中，N=Uα/Uβ。

在△BEO中，用余弦定理并聯(lián)立式（14）和式（15）可得

式中

與Xα的設計類似，式（16）和式（17）中的λmax和 ILM也可被其上限 95%概率值95%λ（上）和L95%I（上）代替。

由式（16）可得出Lβ、Cβ的關系曲線，根據(jù)曲線可對它們進行靈活配置。另外，為便于設計取值，將ξ2與λmax和τ 的關系繪制于圖11中。

圖11　ξ2的三維坐標Fig.11 3-D plots of ξ2

3.3檢測及控制

圖12為該系統(tǒng)的控制框圖。經傅里葉分解易知低通濾波器 LPF的輸出量為負載電流 IL有功分量（ILp）幅值的一半[8]；為主變所期望得到的二次電流，其相量對應圖3中的和為 LC-RPC補償電流的指令量，與之對應的實際值為icα和icβ，它們由滯環(huán)控制器進行控制；直流電壓的誤差信號經PI控制器與的有功分量相加用于對直流電壓的調節(jié)。

圖12　LC-RPC的控制框圖Fig.12 Control diagram of LC-RPC

4 容量分析

對于同一牽引供電系統(tǒng)，RPC與LC-RPC的最大補償電流應相等。故兩系統(tǒng)變流器的設計容量主要取決于各自 conα 的端口運行電壓，更確切地說是變流器直流側電壓。

參考圖 7中的△ACO 可知，負載越重時，

I′cα→IcαM，U′Xα→UXαopt，變流器端口電壓U′cα趨向于其最小值 Ucαopt。另外，從圖 7中△AEO可知，當IcαM變?yōu)?I′cαM后，δαm→δ′αm，這與負載功率因數(shù)降低的情形相對應，顯然，conα 的輸出電壓U′cαopt低于Ucαopt。說明對于固定的直流電壓，采用MOVDM設計后，當牽引饋線的負載越重或功率因數(shù)越低時，LC耦合支路將分擔更多的補償任務，這使得LC-RPC獲得了更充裕的補償能力[23]。而當負荷較輕、功率因數(shù)較高時，其對三相公共電力系統(tǒng)的影響較小，與系統(tǒng)短路容量相比已能滿足國標，可不予以考慮。故將LC-RPC的直流側電壓Udc-LC設計在低于饋線端口峰值電壓如(1.1～1.35)Uα（參考附錄），補償系統(tǒng)即能在絕大部分重載負荷下滿足牽引變電所的電能質量要求，這與工程的期望是相吻合的。

對于RPC情況恰好相反。從圖13中△ABO可知，當負載越重，即Icα越大時，RPC電感上的壓降UL將越大，則conα 的端口電壓UcαL將遠大于Uα。這意味著系統(tǒng)在重載時若需要獲得較好的補償效果，須將RPC的Udc設計得很高，導致主電路所選功率器件的耐壓水平隨之增大，系統(tǒng)的投資成本就越大，而可靠性和運行效率則相應降低。

為定量對比新系統(tǒng)與原系統(tǒng)的節(jié)容效果，在圖13的△ABO中應用余弦定理可得

圖13　RPC的電壓、電流相量圖Fig.13 Votage and current phasor diagram of RPC

令RPC的耦合電抗XL=ξ|Xα-opt|，并連同式（7）一同代入式（8），簡化后可得UcαL的標幺值表達式為

式中，所選取的基值為UB=Uα、IB=IcαM；下標“pu”代表各變量的標幺值。

依據(jù)現(xiàn)有設計經驗，當RPC的單邊補償容量達5～15MV·A時，XL一般為18～25Ω[13-15]，ξ 一般為0.4～0.55。令λmax=0.9（即δαm=57.1°，因為牽引饋線功率因數(shù)的上限95%概率值一般在0.87～0.93），ξ =0.5，由式（19）可得 UcαL-pu與λ和 Icα-pu的關系如圖14所示，其中，基值為UB=Uα、IB=IcαM。

由圖14可知，當λ=0.8（AC-DC型機車的典型值）且Icα=1.0(pu)時，UcαL的最大值為1.408Uα。暫不考慮補償諧波，其直流側電壓 Udc-L需取其峰值[24]，即而 LC-RPC系統(tǒng)的Udc-LC=(1.1～1.35)Uα。由此可見，LC-RPC比傳統(tǒng)RPC有源部分的設計容量減少 45%～32.5%。若考慮補償諧波，LC-RPC的節(jié)容率將進一步擴大。對于AC-DC-AC型電力機車，由于其功率因數(shù)基本位于0.96～0.97區(qū)間，且無諧波的影響，由圖14可知，RPC的 UcαL的最大值約為 1.34Uα，其 Udc-L應設計在1.9Uα左右。此時，LC-RPC有源部分的設計容量將比傳統(tǒng)RPC系統(tǒng)下降41.8%～28.9%。

下面討論變流器的端口視在功率。參考圖 13中的?ABO，考慮一種最保守的情況，即 XL→0、ULα→0和 UcαL→Uα，則 RPC在補償電流為 IcαM的條件下 conα 的額定視在額定功率近似于 UαIcαM，其標幺值為1.0，而從式（9）及圖9可知，按λmax=0.95考慮，Scα的最大值約為 0.63(pu)，說明在最大補償負荷相同情況下，LC-RPC中α相變流器的端口額定視在功率至少比傳統(tǒng)RPC低37%。

從運行使用部門考慮，大功率變流系統(tǒng)市場價格一般為400元/(kV·A)，設牽引變電所的補償容量為10MV·A，傳統(tǒng)RPC需耗資400萬元，LC-RPC的節(jié)容率取40%，則其耗資僅需240萬元。考慮到LC-RPC的直流側電壓遠低于 RPC，其運行損耗和可靠性提高后，后期維護費用還將大幅低于RPC。另外，從設備生產商考慮，直流電壓降低30%～40%后，IGBT的電壓規(guī)格有望降低一個檔次（IGBT一般按額定電壓的300%進行選型），按高電壓規(guī)格的IGBT成本為低一電壓檔次規(guī)格器件的2倍核算[25]，僅IGBT的采購成本一項 LC-RPC就比 RPC降低70%～75%，故前者利潤空間更大，市場競爭更強。

與RPC相比，采用MOVDM后，LC-RPC主電路的設計容量、變流器端口視在功率下降均十分明顯，故新系統(tǒng)在投資成本、系統(tǒng)可靠性、運行損耗、噪聲及電磁輻射水平等主要指標上有較大優(yōu)勢。這也驗證了3.1.1節(jié)中Xα的設計原則（3）。

5 仿真和實驗

5.1仿真

為驗證上述構想，參照圖1搭建了基于單相H橋的RPC和LC-RPC仿真模型。

仿真所使用的某牽引變電所的基本信息如下：三相進線短路容量為530MV·A；主變V/v變壓器電壓比為110×(1±5%) kV∶27.5kV，容量為20.5MV·A （α相為12.5MV·A，β相為10MV·A），α和β相短路阻抗分別為 10.25%和 10.67%。長時間跟蹤測量得到該所牽引變壓器重載相（α相）負載電流 IαL的上、下限 95%概率值分別為αL95%I（上）=282.6A 和功率因數(shù)的上限 95%概率值牽引饋線的端口電壓Uα為29kV。

單相供電時負載將加倍，考慮到系統(tǒng)設計時應留有一定裕量，現(xiàn)將原始設計參數(shù)確定如下

式中，L95%I（下）為負荷的下限95%概率值；Udc-LC、Udc-L分別為LC-RPC、RPC的直流側電壓。這里，Udc-L取為Uα的2.3倍。因為所測量的負載電流中存在大量諧波，若取2倍，將達不到預期效果，詳見仿真結果。

由式（20）及前述設計方法可得系統(tǒng)的仿真參數(shù)見表1，其中，C為變流器直流側電容，L為RPC的耦合電感。

表1　仿真參數(shù)1Tab.1 Simulation parameters 1

圖15　滿足條件的Lβ和CβFig.15 Available Lβand Cβ

仿真負載的參數(shù)見表2。iαL1模擬負荷電流的下限 95%概率值；iαL2模擬中等負荷時的負載情況；iαL1+iαL2作為第三種工況，用來模擬重載時兩補償系統(tǒng)的特性（主要為負荷的上限95%概率電流值）。系統(tǒng)的仿真結果如圖16～圖24所示。

表2　仿真參數(shù)2Tab.2 Simulation parameters 2

圖16　無補償裝置時系統(tǒng)的波形Fig.16 Waveforms without compensation

圖17　投入RPC后系統(tǒng)的波形（Udc-L=66.7kV）Fig.17 Waveforms with RPC (Udc-L=66.7kV)

圖18　投入LC-RPC后系統(tǒng)的波形（Udc-LC=38.9kV）Fig.18 Waveforms with LC-RPC (Udc-LC=38.9kV)

圖19　一次電流波形Fig.19 Primary side waveforms

將圖17、圖 18與圖16相比可知，投入RPC 和 LC-RPC后系統(tǒng)一次電流趨于對稱的三相正弦波，功率因數(shù)≈1，而且重載時牽引饋線的電壓有效值明顯提升。故RPC和LC-RPC均能有效應對電氣化鐵路供電系統(tǒng)的主要電能質量問題（雖然重載時RPC的諧波補償效果稍遜于LC-RPC）。然而，由于Udc-LC=38.9kV約為Udc-L=66.7kV的58.3%，LC-RPC的設計容量比RPC低42%，其成本優(yōu)勢顯著。若將RPC的設計直流電壓降13%至2Uα，即58kV，則重載時一次電流已經不能平衡（見圖19a），此時的RPC已達不到補償要求（電壓不平衡度＞2%）。

另外，當 LC-RPC的直流電壓從 38.9kV降至38.3kV時，從圖19b可以看出，LC-RPC的基波補償效果基本不變，僅諧波補償效果在負荷較輕時有下降，而負荷較重時基本不變。這證明了采用MOVDM 設計的 LC-RPC具有出色的重載補償能力，與工程期望是相吻合的。若系統(tǒng)短路容量較大，且輕載時諧波對三相系統(tǒng)的影響較小，則可將Udc-LC進一步降低。另外，在控制算法中將補償量中的基波和諧波分離開，使LC-RPC僅對負序和無功進行補償，則 Udc-LC還可進一步降低（類似的檢測方法已有較多文獻報道，筆者不再贅述）。

5.2實驗

為進一步驗證LC-RPC的正確性，搭建了一個小容量實驗室系統(tǒng)對其進行驗證。主變容量為40kV·A，變比分別為 380V∶380V（α相）和 380V∶127V（β相）。采用相控型單相整流器+阻感負荷模擬牽引負荷，調整觸發(fā)延遲角，將其功率因數(shù)穩(wěn)定在0.85左右。數(shù)字控制器為 TMS320F2812，采樣頻率為12.8kHz。兩逆變器為單相H橋，IGBT的規(guī)格為1200V/ 450A。測試儀器為 HIOKI-3196電能質量分析儀。其他參數(shù)見表3。實驗波形如圖20～圖24所示。

表3　實驗參數(shù)Tab.3 Experiment parameters

圖20　無補償裝置時系統(tǒng)的實驗波形Fig.20 Experimental waveforms without compensation

圖21　投入RPC后系統(tǒng)的穩(wěn)態(tài)波形（Udc-L=820V）Fig.21 Waveforms with RPC (Udc-L=820V)

圖22　投入LC-RPC后系統(tǒng)的穩(wěn)態(tài)波形（Udc-LC=490V）Fig.22 Waveforms with LC-RPC (Udc-LC=490V)

圖 21、圖 22為兩系統(tǒng)的穩(wěn)態(tài)電流波形，表 4為穩(wěn)態(tài)時的實驗結果數(shù)據(jù)。對比無補償時的電流實驗波形（見圖20）可知，RPC和LC-RPC均能有效抑制非線性單相負荷滲透至主變一次側的負序、無功和諧波。但是 Udc-LC=490V 約為 Udc-L=820V 的59.8%，這驗證了LC-RPC的容量上的優(yōu)勢。另外，由圖23、圖24所示的動態(tài)波形可知，當常規(guī)RPC 的Udc-L從820V下降20%至 656V，雖然仍高于峰值電壓但RPC的補償效果已經非常明顯。但若將LC-RPC的Udc-LC從490V下降44%至275V后，LC-RPC的補償效果不明顯。若此種負荷對應于系統(tǒng)的最大負荷，則將 Udc-LC設計成 490V將能滿足大部分重載負荷的補償要求，這進一步驗證了上述結論的正確性。

表4　實驗結果數(shù)據(jù)Tab.4 Experiment results data

圖23　RPC的動態(tài)電流波形Fig.23 Dynamic current waveforms of RPC

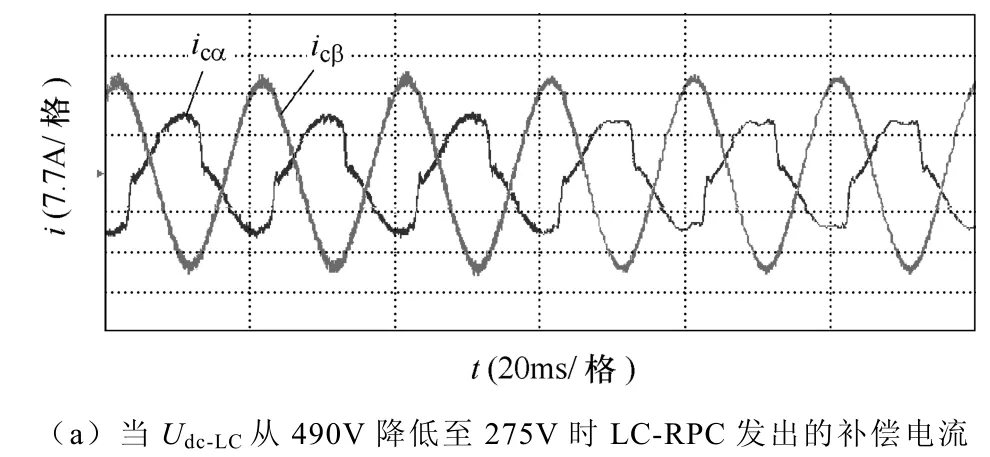
圖24　LC-RPC的動態(tài)電流波形Fig.24 Dynamic current waveforms of LC-RPC

6 結論

本文提出一種適用于單相牽引供電系統(tǒng)的 LC耦合的電氣化鐵道電能質量綜合控制系統(tǒng)。簡述了系統(tǒng)的補償原理和控制策略，并對變流器端口運行特性進行了系統(tǒng)分析。在此基礎上給出適應于電鐵隨機波動性負荷的 LC耦合支路的設計方法，并對系統(tǒng)的容量特性進行了詳細分析，分析結果表明LC-RPC的節(jié)容能力出色。最后，結合實測數(shù)據(jù)給出了系統(tǒng)參數(shù)的設計實例，并開展了仿真和實驗研究，其結果驗證了LC-RPC補償效果及節(jié)容能力的有效性。

由于LC-RPC充分挖掘了LC耦合支路的潛能，使得該系統(tǒng)在重載下能獲得較好補償效果，且大幅降低了變流器的容量。加之主變結構簡單、容量利用率高，故該系統(tǒng)是一種具有較高性價比和可靠性的電氣化鐵道電能質量綜合控制系統(tǒng)。

附 錄

附圖1為采用MOVDM后，當補償電流取上、下限95%概率值且時LC-RPC中conα 的相量。參考附圖1及式（10）可知，與對應的 LC 耦合支路的電壓降UAC、UAB分別為

附圖1 采用MOVDM后conα的相量App. Fig.1 Phasor diagram of conα using MOVDM

在附圖 1的△ABO中應用余弦定理，并考慮到式（A1）和式（13），易求得變流器的最大端口電壓UcαM為

在實際系統(tǒng)中k分布在0.2～0.5區(qū)間的概率以及λmax分布在0.87～0.93區(qū)間的概率較其他值高。由附圖2可知，將Udc-LC設計在區(qū)間(1.1～1.35)Uα已能滿足絕大部分負荷的補償要求。

[1] 武中, 王志剛, 宋述勇, 等. 電氣化鐵道牽引變電所對電力系統(tǒng)影響及治理的仿真研究[J]. 中國電機工程學報, 2011, 31(9): 77-82. Wu Zhong, Wang Zhigang, Song Shuyong, et al. Simulation research on the influence and management of the electrified railway traction substation on power system[J]. Proceedings of the CSEE, 2011, 31(9): 77-82.

[2] 姚宗溥, 侯世英, 祝石厚. 電氣化鐵路牽引負荷對固原電網的影響[J]. 電網技術, 2007, 31(1): 15-19. Yao Zongpu, Hou Shiying, Zhu Shihou. Influence of electrical railway’s traction load on Guyuan power network[J]. Power System Technology, 2007, 31(1): 15-19.

[3] 國家標準化管理委員會. GB/T 15543—1995 中國標準書號[S]. 北京: 中國標準出版社, 2005.

[4] 張志文, 王耀南, 劉福生, 等. 多功能平衡牽引變壓器運行方式研究[J]. 中國電機工程學報, 2004, 24(4): 125-132. Zhang Zhiwen, Wang Yaonan, Liu Fusheng, et al. Study on operational mode of multi-function balance traction transformer[J]. Proceedings of the CSEE, 2004, 24(4): 125-132.

[5] 張志文, 王耀南. 星形-三角形聯(lián)結三相變兩相和三相變三相平衡變壓器[J]. 電工技術學報, 2006, 21(11): 82-86. Zhang Zhiwen, Wang Yaonan. A novel three-phase to two-phase and three-phase balance transformer inand △ connection[J]. Transactions of China Electrotechnical Society, 2006, 21(11): 82-86.

[6] Raygani S, Tahavorgar A, Fazel S, et al. Load flow analysis and future development study for an AC electric railway[J]. IET Electrical Systems in Transportation, 2012, 2(3): 139-147.

[7] 劉釗, 劉邦銀, 段善旭, 等. 系統(tǒng)電壓不平衡下鏈式靜止同步補償器控制研究[J]. 中國電機工程學報, 2011, 31(9): 1-7. Liu Zhao, Liu Bangyin, Duan Shanxu, et al. Research on cascade multilevel STATCOM under unbalanced system voltage[J]. Proceedings of the CSEE, 2011, 31(9): 1-7.

[8] 胡斯佳, 張志文, 李勇, 等. 一種繞組補償式電氣化鐵道電能質量控制系統(tǒng)[J]. 中國電機工程學報, 2014, 34(13): 2140-2150. Hu Sijia, Zhang Zhiwen, Li Yong, et al. An winding compensation based electrified railway power quality control system[J]. Proceedings of the CSEE, 2014, 34(13): 2140-2150.

[9] 張定華, 桂衛(wèi)華, 王衛(wèi)安, 等. 新型電氣化鐵道電能質量綜合補償系統(tǒng)的研究及工程應用[J]. 電工技術學報, 2009, 24(3): 189-194. Zhang Dinghua, Gui Weihua, Wang Weian, et al. Study and application of a new power quality combined compensation system for electrified railway[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 189-194.

[10] 張宇, 陳喬夫, 李江紅. 一種用于電氣化鐵道無功補償?shù)目煽仉娍蛊鱗J]. 電工技術學報, 2011, 26(8):166-171. Zhang Yu, Chen Qiaofu, Li Jianghong. A controllable reactor for reactive power compensation of electrified railways[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 166-171.

[11] 張鑫, 江全元. 基于V/V接線變壓器的鐵路功率調節(jié)器容量配置和能量優(yōu)化補償策略[J]. 電力自動化設備, 2014, 34(1): 102-108. Zhang Xin, Jiang Quanyuan. Capacity configuration of V/V transformer-based railway power conditioner and optimal energy compensation strategy[J]. Electric Power Automation Equipment, 2014, 34(1): 102-108.

[12] 朱紅萍, 李燕, 王俊年. 基于感應濾波變壓器的混合有源補償電流平衡裝置[J]. 電工技術學報, 2013, 28(8): 265-275. Zhu Hongping, Li Yan, Wang Junnian. A hybird active compensation device for current balance based on inductive filtering transformer[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 265-275.

[13] Horita Y, Morishima N, Kai M, et al. Single-phase STATCOM for feeding system of Tokaido Shinkansen[C]//International Power Electronics Conference, 2010: 2165-2170.

[14] 志々目浩一. 在來線用電力補償裝置（RPC）の実用[J]. 明電時報, 2011, 333(4): 58-62.

[15] 兎束哲夫. 電圧不平衡補償裝置[J]. 鉄道技術, 2009, 3(58): 34-35.

[16] 袁佳歆, 李士杰, 張晨萌, 等. 電氣化鐵路三相不平衡協(xié)同補償[J]. 電工技術學報, 2011, 26(1): 218-223. Yuan Jiaxin, Li Shijie, Zhang Chenmeng, et al. Research on collaborative compensation of electrified railway’s three-phase unbalanced load[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 218-223.

[17] 鄭建勇, 張愉, 丁祖軍. 并聯(lián)電感型混合有源濾波器及其控制策略[J]. 電網技術, 2010, 34(1): 90-97. Zheng Jianyong, Zhang Yu, Ding Zujun. A novel parallel inductor type hybrid active power filter and its control strategy[J]. Power System Technology, 2010, 34(1): 90-97.

[18] 劉健犇, 陳喬夫, 代少君, 等. 串聯(lián)混合型有源濾波器直流母線電壓控制策略[J]. 電工技術學報, 2012, 27(9): 54-61. Liu Jianben, Xiong Qiaofu, Dai Shaojun, et al. DC-link voltage control strategy of series hybrid active power filter[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 54-61.

[19] 孫佐, 王念春, 許衛(wèi)兵. 一種高性價比并聯(lián)混合有源電力濾波器[J]. 中國電機工程學報, 2007, 27(36): 79-84. Sun Zuo, Wang Nianchun, Xu Weibin. A parallel hybrid active power filter with good cost performance[J]. Proceedings of the CSEE, 2007, 27(36): 79-84.

[20] Wiroj T, Hatada T, Wada K, et al. Design and performance of a transformerless shunt hybrid filter integrated into a three-phase diode rectifier[J]. IEEE Transactions on Power Electronics, 2007, 22(5): 1882-1889.

[21] Casanellas F. Losses in PWM inverters using IGBTs[J]. Proceedings of Electric Power Applications, 1994, 14(5): 235-239.

[22] Richardeau F, Pham T. Reliability calculation of multilevel converters: theory and applications[J]. IEEE Transactions on Power Electronics, 2013, 60(10): 4225-4233.

[23] Remus T, Marco L, Pedro R. Grid converters for photovoltaic and wind power systems[M]. Chi-Chester: IEEE Press, 2011.

[24] Rashid M H. Power electronics handbook[M]. 3rd ed. London: Butterworth-Heinemann, 2011.

[25] Bin Wu. High-power converter and AC drivers[M]. New Jersey: IEEE Press, 2006.

An LC-Coupled Electric Railway Static Power Conditioning System

Hu Sijia Zhang Zhiwen Li Yong Luo Longfu Luo Pei
（College of Electrical and Information Engineering Hunan University Changsha 410082 China）

To improve power quality and overcome excessive neutral sections in traditional two-phase traction supply system, single-phase traction supply system adopting railway static power conditioner (RPC) is a feasible solution. However, relatively high power capacity limits its large scale industrial application. To enhance the cost-efficiency and reliability of the compensation system, a LC-coupled RPC (LC-RPC) is proposed in this paper. Based on the operating properties of LC-RPC, a minimum operating voltage design for LC-coupling branch is proposed, which is suitable for the fluctuating railway load. And then, a detailed capacity comparison between LC-RPC and RPC is discussed as well. The results indicate that the LC-RPC is better to decrease capability than RPC. Finally, based on the measured data of a traction substation, the effectiveness of LC-RPC and its ability of capacity decreasing have been verified.

LC-coupling, railway static power conditioner, parameter design, power capacity analysis, power quality

TM76

胡斯佳 男，1987年生，博士，助理教授，研究方向為電氣化鐵道電力系統(tǒng)電能質量與潮流控制、大功率多電平變流器和 FACTS技術。

E-mail: huda_hsj@163.com

張志文 男，1963年生，教授，博士生導師，研究方向為交、直流電源電能變換系統(tǒng)理論與新技術、電氣化鐵道電能質量分析與控制、電力系統(tǒng)諧波抑制。

E-mail: hdzzw@126.com（通信作者）

國家自然科學基金（51477046、51377001），國家科技支撐計劃（2013BAA01B01），湖南省戰(zhàn)略性新興產業(yè)科技攻關項目（2014GK1037）和國家電網公司項目（5216A014007V）資助。

2014-03-10 改稿日期 2014-06-19