基于局部密度估計的聚類個數確定研究

龍章勇

（南京鐵道職業技術學院，江蘇　南京　210031）

基于局部密度估計的聚類個數確定研究

龍章勇

（南京鐵道職業技術學院，江蘇南京210031）

隨著人工智能和數據挖掘技術的興起，聚類分析已被廣泛應用于通信、文本數據統計、生物信息學和圖像處理中。對于非監督聚類分析，聚類的分類數目是決定聚類質量的關鍵因素。通常聚類個數事先無法確定，隨即選擇的初始聚類中心容易使聚類結果不穩定。針對此，基于聚類中心具有高局部密度且距高局部密度聚類中心距離較遠的特點，提出一種基于局部密度估計的聚類個數的估計方法。經過仿真實驗，驗證了該算法具有良好的有效性和魯棒性。

聚類個數；密度峰值估計；聚類有效性；聚類分析

隨著計算機和互聯網應用的普及，信息和數據爆炸似的增長，復雜的多種信息數據也可以作為很重要的研究內容。從海量數據的研究和挖掘中提取出互有關系的信息變得非常重要，甚至決定了社會科技的發展。聚類算法作為數據分析的主要工具，已在多方面被廣泛地研究和應用。

1　聚類有效性分析與聚類個數估計

1.1聚類有效性分析

現在常用的估計聚類個數的有效性評價方法大概有3種：有效性指標、檢測穩定聚類結構的穩定性方法和系統演化方法。其中，有效性指標在實際中應用廣泛，包括Silhouette指標、Davies-Bouldin指標、Calinski-Harabasz指標、加權的類間類內相似度比率和Homogeneity-Separation指標等。

1.1.1平均Silhouette（Sil）指標。設a（t）為聚類Cj中的樣本t與類內所有其他樣本的平均不相似度或距離，d（t，Ci）為樣本t到另一個類Ci的所有樣本的平均不相似度或距離，則b（t）=min｛d（t，Ci）｝，i=1，2，……，k；i≠j［1］。Sil指標計算每個樣本與同一聚類中樣本的不相似度以及與其他聚類中樣本的不相似度，其每個樣本t的計算公式如下：

一般以一個數據集的所有樣本的平均Sil值來評價聚類結果的質量，Sil指標越大，表示聚類質量越好，其最大值對應的類數作為最優的聚類個數。

1.1.2Davies-Bouldin（DBI）指數。DBI指數是基于樣本的類內散度與各聚類中心間距的測度，進行類數估計時其最小值對應的類數作為最優的聚類個數。設DWi表示聚類Ci的所有樣本到其聚類中心的平均距離，DCij表示聚類Ci和聚類Cj中心之間的距離，則DB指標如下：

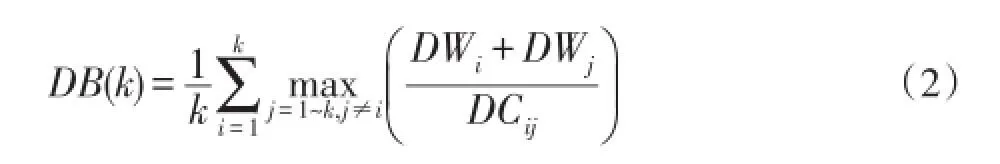
1.1.3Calinski-Harabasz（CH）指標。CH指標（偽F統計量）是基于全部樣本的類內離差矩陣與類間離差矩陣的測度，其最大值對應的類數作為最優的聚類個數，則CH指標如下：

其中，SSB和SSw分別表示類間離差矩陣和類內離差矩陣，k為聚類數目。類間離差矩陣SSB定義如下：

其中，mi，m分別表示第i個類的中心和類內平均，||mi-m||定義了向量之間的歐式距離。類內離差矩陣SSw的定義如下（也稱為Hartigan指標）：

其中，x，Ci分別表示數據點和第i個類。

從定義可以看出：好的聚類結果，是希望SSB越大越好和SSw越小越好。因此，CH（k）的值越大，選擇的k值越接近最優。

1.2聚類數目對有效性的影響

對于盲聚類分析，聚類數目和聚類初始中心對于結果的影響很明顯，因為目前采用的聚類算法，類似于K-均值聚類，都對類數和初始聚類中心敏感。

不失一般性，對同一組數據集合，分別采用目標類數為3～5進行K-均值聚類，仿真的對比結果如圖1所示。

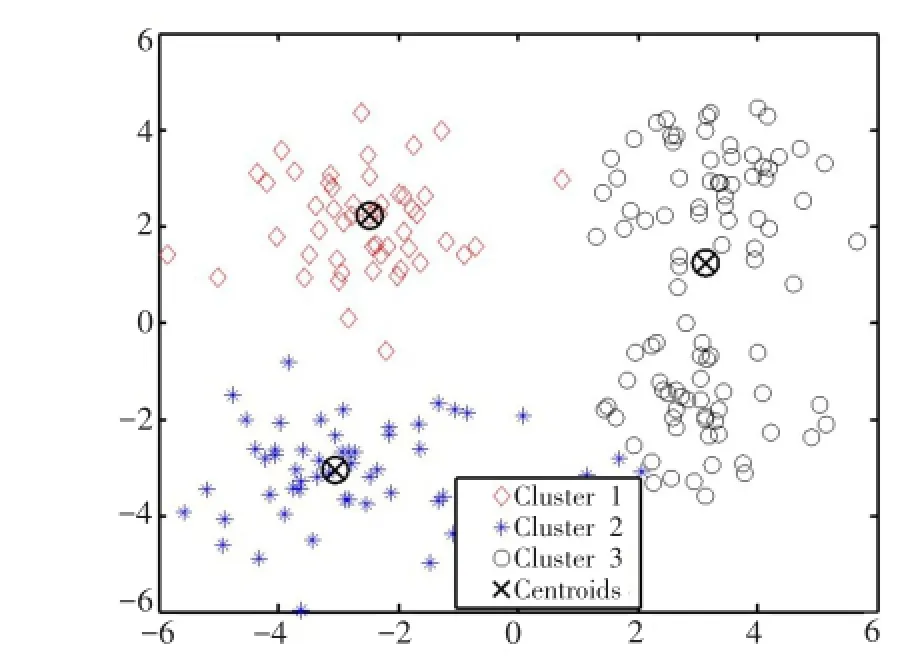
（a）采用k=3聚類的結果

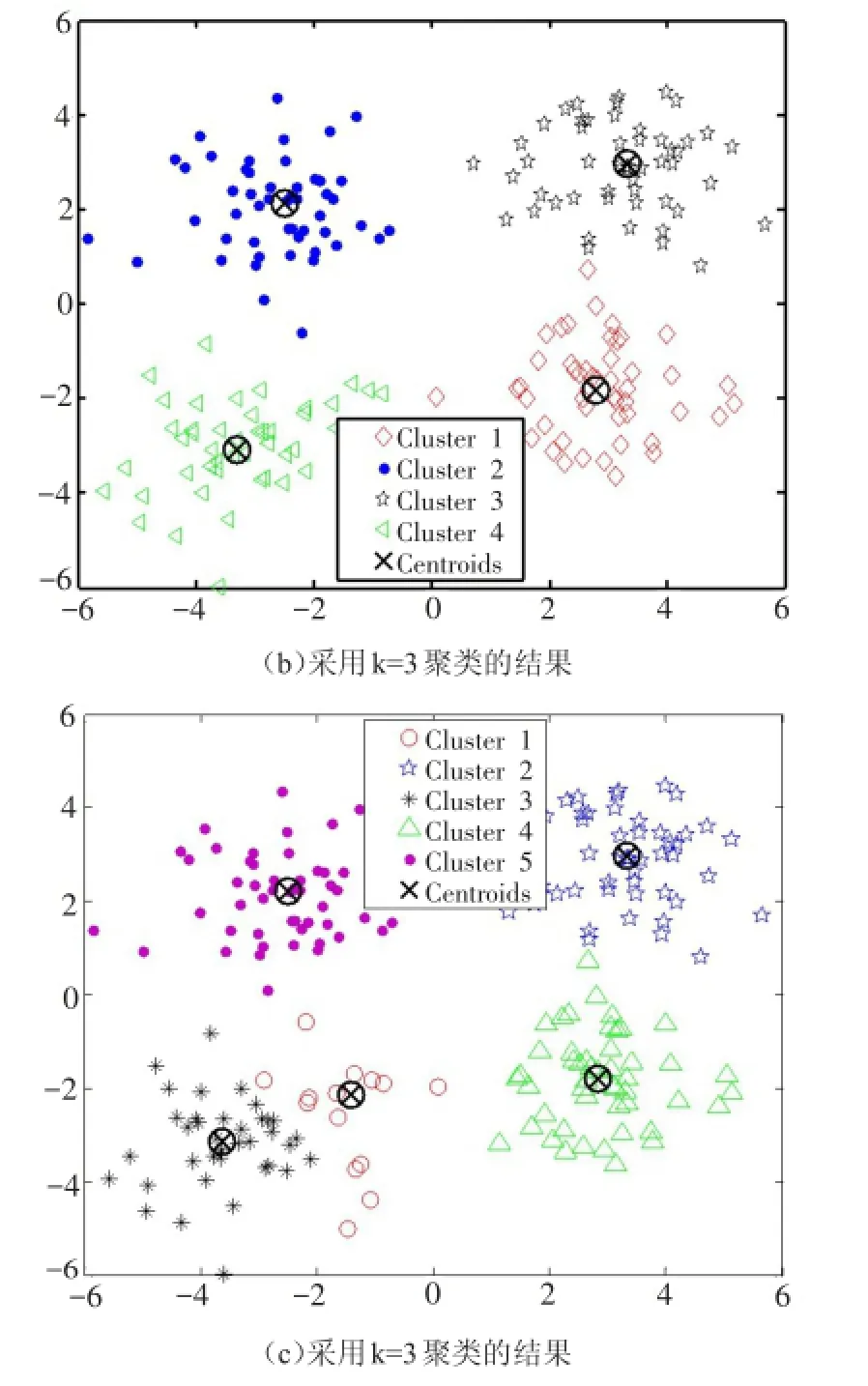
圖1　不同類數下的K均值聚類結果

為了對比不同聚類數目下的聚類結果的性能指標，對上述實驗數據，分別采用2.1節中的指標進行評估，結果如圖2所示。從圖2可以看出，前3種指標顯示，選擇類數為4最接近最優的聚類目標。但是采用Hartigan指標，其結果不然。

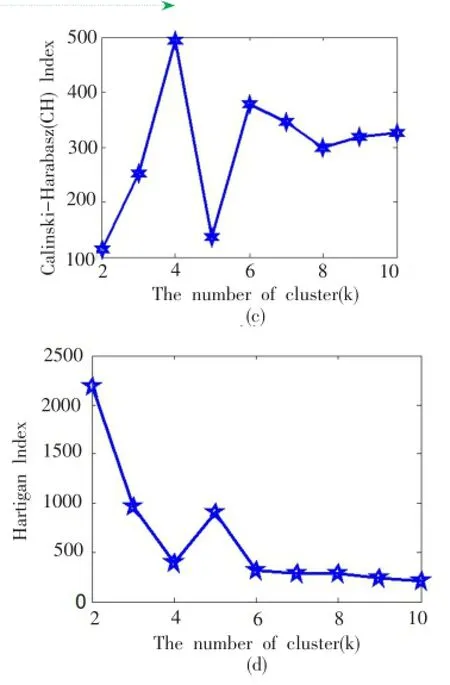
圖2　4種有效性指標估計結果

上述實驗中，不同的指標所側重的測度是不一致的，從而適用的應用場景也是有區別的。另外，從相鄰類數下指標的走勢可以看出，K-均值算法對于類數敏感性顯而易見。因此，在聚類之前，能夠確定有效的聚類數目是非常必要和重要的。

2　基于局部密度估計的聚類個數確定

給定點集S，對于每一個樣本點i，為其定義2個屬性參量：局部密度ρi和距離高密度點集的距離δi。樣本點i的局部目的ρ定義如下：

其中，dij為樣本點i和樣本點j之間的“距離”度量，并且滿足三角不等式；dc是常數參數，定義為截止距離，其物理意義是控制樣本點的影響最遠距離。式（6）中函數R（x）的定義如式（7）：

其中，ρi表示距離i的距離小于dc的樣本點數量。i的參數δi計算如下：

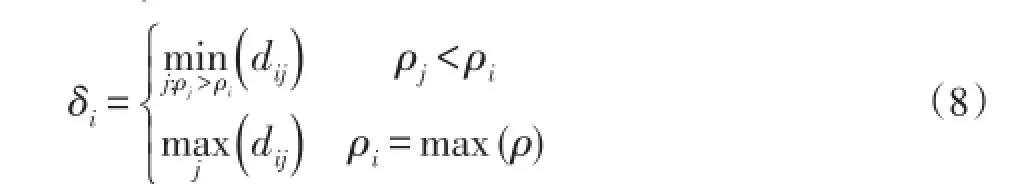
其中，max（ρ）為點集S的最大局部密度。從式（8）可以看出，對于非最大局部密度樣本點，δi定義為樣本點i距離其他任意更高局部密度樣本點的最小距離；而對于最大局部密度樣本點，δi定義為其他點到此點的最大距離。

通過對點集S中的樣本經行二維空間的處理，以 ρi和δi兩個指標對點集降維處理。其中，ρi用來限制點集在多維測度空間內的局部密度，而δi用來度量局部密度較大的多維點集在測度空間內的相對聚類。距離其他高局部密度較“遠”的點，稱為在決策圖上的“孤點”。“孤點”的個數即是聚類的估計類數。在局部密度的估計中，截止距離dc的選擇非常重要，其影響了局部密度測度空間的邊界。對于dc的選擇準則，還需要進一步的理論分析，但是多次實驗證明，dc的選擇需要保證局部密度的最小取值不小于點集總數的1%～2%。

3　實驗結果與分析

對于2.2中所采樣的同樣的數據數據集合，使用2中介紹的基于局部密度估計的方法，計算點集中每個樣本的ρi和δi兩個指標，繪出決策圖如圖3所示。

從圖3可以看出，在ρi和δi兩個指標都很“突出”的區域有4個明顯的“孤”點。所以，估計算法確定出的聚類數目為k=4。對于2.2節的結論，兩者的結論是一致的。通過對多組數據的實驗，該文所提出的算法估計出的聚類類數和Sil指標、DBI指標和CH指標的一致率分別是99.4%、99.1%和98.8%。

圖3　基于局部密度估計的決策圖

4　結論

從K-均值算法對于聚類個數和初始中心敏感的缺陷出發，基于聚類中心具有高密度且距高局部密度聚類中心具有較遠距離的特點，提出一種基于局部密度估計的聚類個數的估計方法。經過仿真實驗，驗證了該算法具有良好的有效性和魯棒性。

Cluster Number Estimation Based on Local Density Estimator

Long Zhangyong
（Nanjing Institute of Railway Technology，Nanjing Jiangsu 210031）

With the development of artificial intelligence and data mining technology，cluster analysis has been widely used in many fields，which range from communication to bioinformatics，bibliometrics，and image processing.For unsupervised clustering analysis，the number of clusters is the key factor to determine the quality of clustering.Usually the number of clusters can not be determined in advance，then the initial cluster center is easy to make that the clustering result is not stable.For this，based on the characteristic that the cluster centers have a high local density and a relatively large distance from the high local density clustering center，a new method for estimating the number of clusters based on local density estimation was proposed.The simulation showed that the proposed algorithm performance was effective and robust.

cluster number；density peaks estimator；cluster validation；cluster analysis

TP18

A

1003-5168（2016）05-0026-03

2016-04-18

中國職教學會軌道交通專業委員會科研基金（201419）；全國教育信息技術研究十二五規劃課題（136231366）。

龍章勇（1979-），男，碩士，講師，研究方向：無線通信技術。

［1］Kaufman L，P J Rousseeuw.Finding Groups in Data：An Introduction to Cluster Analysis［M］.Hoboken，NJ：John Wiley&Sons，Inc.，1990.