基于PCA—GRNN神經(jīng)網(wǎng)絡的露天礦邊坡穩(wěn)定性分析

閆守志　郭紹征　陳勇智　趙建強　倪澤雨

摘 要：露天礦邊坡穩(wěn)定性分析是一個復雜的非線性、不確定的動態(tài)系統(tǒng)，各因素之間具有一定的相關性。首次應用主成分與GRNN神經(jīng)網(wǎng)絡結合的原理和方法，建立了邊坡穩(wěn)定性評價模型，能定量得出各主成分對邊坡穩(wěn)定性的影響程度。利用PCA-GRNN神經(jīng)網(wǎng)絡評價模型對邊坡安全系數(shù)進行了預測，并與真實值進行了對比分析，得出了PCA-GRNN方法評價精度較高、相對誤差較小。由此可見，該模型在邊坡穩(wěn)定性的分析中具有較高的可行性和適用性。

關鍵詞：邊坡穩(wěn)定性；主成分分析；GRNN神經(jīng)網(wǎng)絡；特征根

中圖分類號：TD854.6 文獻標識碼：A DOI：10.15913/j.cnki.kjycx.2016.16.013

露天礦邊坡穩(wěn)定性分析是工程界和學術界關注的重要課題，但各因素間的交互作用在單因素分析的方法中已被忽略，無法很好地符合實際情況。國內(nèi)外使用較為廣泛的邊坡穩(wěn)定性分析方法主要有數(shù)值分析法、極限平衡法等。這些方法都需綜合考慮影響邊坡穩(wěn)定的主要因素，其過程比較復雜，計算煩瑣，無法準確地描述邊坡的非線性特征。由于計算機技術的不斷進步，關于邊坡穩(wěn)定性評價的方法得到了的改進，一些復合評價方法也被逐漸應用到了邊坡穩(wěn)定性的分析中。馮夏庭等人提出了邊坡穩(wěn)定性的神經(jīng)網(wǎng)絡估計方法。 主成分分析方法應用已較為成熟，但運用主成分對邊坡穩(wěn)定性的研究較為缺乏。

1 主成分分析法的基本思想

在對實際問題研究的過程中，一般情況都是關于n個樣本，每個樣本包含p個隨機變量的問題，數(shù)學上的處理方式為將原始的p個變量作線性組合。作為新的變量，設p個原始變量為x1，x2，…，xp，對應的新的變量（主成分）為y1，y2，…，yp.

主成分方差貢獻率為某個特征根占總特征的根比例。設特征根為λ，則第i個主成分所對應的方差貢獻率為：

特征值累計貢獻率一般要求在75%～85%，其中，特征值即主成分的個數(shù)小于5或6.主成分分析是將原來多個變量化為少數(shù)幾個綜合指標的一種統(tǒng)計分析方法。從數(shù)學角度看，這是一種降維處理技術。假定有n個地理樣本，每個樣本共有p個變量描述，這樣就構成了一個n×p階的數(shù)據(jù)矩陣。

2 GRNN神經(jīng)網(wǎng)絡的基本思想

廣義回歸線性網(wǎng)絡GRNN的主要優(yōu)點在于學習快速，是一種基于非線性回歸理論的前饋式神經(jīng)網(wǎng)絡模型。當樣本數(shù)量非常大時，GRNN神經(jīng)網(wǎng)絡能實現(xiàn)快速逼近，處理實時環(huán)境中的稀疏數(shù)據(jù)時非常有效。目前，該神經(jīng)網(wǎng)絡在系統(tǒng)辨識和預測控制等方面得到了應用。

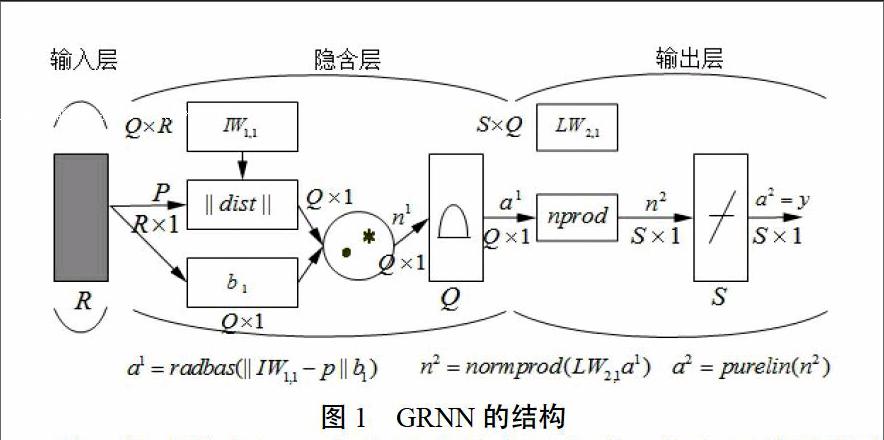
GRNN的結構如圖1所示。

其一般由輸入層、隱含層和輸出層組成。輸入層能將樣本變量傳遞到隱含層，將不參與真實運算。隱含層所含神經(jīng)元個數(shù)是訓練集樣本數(shù)，其權值為歐氏距離函數(shù)（ ），作用是為計算網(wǎng)絡輸入與第一層的權值IW1，1間的距離，b1為隱含層閥值。使用徑向基函數(shù)作為隱含層傳遞函數(shù)，一般采用高斯函數(shù)為傳遞函數(shù)。網(wǎng)絡中第三層為線性輸出層，其權函數(shù)為規(guī)范化點積權函數(shù)（用nprod表示），計算網(wǎng)絡的向量為n2，其每個元素就是向量a1和權值矩陣LW2，1每行元素的點積再除以向量a1的各元素之和得到的，并將結果n2提供給線性傳遞函數(shù)a2=purelin（n2），計算網(wǎng)絡輸出。

3 邊坡影響因素間的相關性分析

本文所選取巖土體的重度γ、巖土體的黏聚力c、內(nèi)摩擦角f、邊坡的坡角α，邊坡的高度H以及孔隙壓力μ作為影響邊坡穩(wěn)定的主要因素。從大量參考文獻得出邊坡穩(wěn)定性評價的輸出因素為邊坡安全系數(shù)。

由于各指標對應的變量因子所采取的單位標準不一樣，因此，各變量之間無法直接比較，對數(shù)據(jù)標準化處理需要在進行主成分分析前進行。其中，SPSS主要使用z-score標準化法，可將數(shù)據(jù)統(tǒng)一映射到[-1，1]區(qū)間上。方差分解主成分提取分析結果如表1所示。

表1中，利用SPSS提取出2個主成分，且方差累計貢獻率大于75%，所以，提取的主成分有效。近一步借助其求得主成分因子的載荷矩陣，具體如表2所示。

由于利用SPSS進行主成分分析時，無法直接得出主成分的系數(shù)。表2中主成分載荷矩陣并不是主成分的特征向量，其系數(shù)的準確求法則為：各個主成分載荷除以表1中各個主成分所對應特征值的算術平方根。根據(jù)主成分分析模型和因子載荷，可以得到提取的2個主成分與原先6個指標變量之間的線性組合，表達式如下：

4 PCA-GRNN預測數(shù)值實例

由于輸入數(shù)據(jù)具有一定相關性和輸入數(shù)據(jù)過多，所以，本文將主成分分析法與GRNN神經(jīng)網(wǎng)絡相結合，構建了優(yōu)選模型，并對邊坡安全狀態(tài)進行有效了分析。將18組數(shù)據(jù)作為訓練樣本子集，預測樣本子集的11組邊坡數(shù)據(jù)。該案例分析中的學習速率設為0.01，最大迭代次數(shù)為2 000，誤差性能目標為0.000 001.分別運用兩種算法對邊坡的安全性進行了比較分析，結果如表3所示。

通過對兩種預測方法所預測結果的平均值、最小值以及最大值的比較可以得出，PCA-GRNN算法比PCA-BP算法的預測結果更為準確。由此額空間，該方法在邊坡穩(wěn)定性分析上較為有效、合理。

兩種方法的預測值與實際測量值之間的誤差關系如圖2所示。

由此可見，利用PCA-GRNN模型進行評價比利用PCA-BP得出的預測值精度更高、相對誤差更小。該模型在邊坡穩(wěn)定性分析中具有較好的可行性和適用性。

5 結論

以PCA-GRNN方法描述了分類結果與樣本值兩者間的映射關系，給出了具體的概率累計表達式與模型建立的方法，并通過對某一工程實例的驗證得出，采用PCA-GRNN模型描述邊坡穩(wěn)定性分類指標與穩(wěn)定性之間的經(jīng)驗關系，其建模方法簡單，易于實現(xiàn)。與BP神經(jīng)網(wǎng)絡相比，GRNN網(wǎng)絡優(yōu)勢在于訓練不需要迭代、隱含層所含神經(jīng)元個數(shù)由訓練樣本可自適應確定，避免了BP神經(jīng)網(wǎng)絡在迭代中的權值修改，且對接近于局部神經(jīng)元特征的輸入具有很強的吸引力等。

參考文獻

[1]胡敏萍.極限平衡法和有限單元法分析復雜邊坡的穩(wěn)定性[D].杭州：浙江大學，2004.

[2]郭子儀，范振華，朱云升，等.邊坡穩(wěn)定性分析中的有限元極限平衡法[J].武漢理工大學學報（交通科學與工程版）， 2014，38（01）.

[3]馮夏庭，王泳嘉.邊坡穩(wěn)定性的神經(jīng)網(wǎng)絡估計[J].工程地質(zhì)學報，1995，3（04）.

[4]熊海豐.基于人工神經(jīng)網(wǎng)絡技術的邊坡穩(wěn)定性評價研究[D].武漢：武漢理工大學，2003（05）.

[5]張表志.基于主成分分析的大型棄土場邊坡穩(wěn)定性敏感因素分析[J].公路交通科技（應用技術版），2013（07）.

[6]谷瓊，蔡之華，朱莉.基于PCA-GEP算法的邊坡穩(wěn)定性預測[J].巖土力學，2009，30（03）.

[7]張文霖.主成分分析在SPSS中的操作應用[J].市場研究，2005（12）.

[8]張紹紅.概率神經(jīng)網(wǎng)絡技術在地震巖性反演中應用[J].遼寧工程技術大學學報，2007（26）.

[9]蘭海濤，李謙，韓春雨.基于廣義回歸神經(jīng)網(wǎng)絡的邊坡穩(wěn)定性評價[J].巖土力學，2009，30（11）.

[10]陳建宏，鄭榮凱，陳浩.基于PCA和BP神經(jīng)網(wǎng)絡邊坡穩(wěn)定性分析[J].中國安全生產(chǎn)科技術，2014（05）.

〔編輯：張思楠〕