導體的電阻效應與超導理論

武圓

（北京人文大學　理工學院，北京101300）

導體的電阻效應與超導理論

武圓

（北京人文大學理工學院，北京101300）

通過對導體電阻成因的分析，得到導體超導態第一轉變溫度需滿足的條件是在該溫度下導體中的電子都應處于束縛態。根據束縛態電子在電場中的Stark效應，解釋超導態電子的微觀輸運圖像，進而得出導體超導態轉變第一溫度的數學表達式。超導體原子的熱振動（聲子）對原子間的軌域相干有破壞作用，即原子的熱振動也是限制超導態轉變臨界溫度的因素，經過分析得到了關于原子熱振動的超導態轉變第二溫度，該轉變溫度體現的是原子熱振動對超導態轉變的制約作用。

超導轉變溫度；相干；聲子；束縛態

1911年，昂納斯發現Hg的電阻在4.2 K時突降到當時的儀器已無法測出的程度，這是人們第一次觀察到超導現象，這一發現開拓了一個嶄新的物理領域。1957年，Bardeen、Cooper和Schrieffer［1］提出了著名的BCS理論，該理論雖然僅能對40 K以下的超導體做出較好的解釋，但對超導研究仍然起到了很大的促進作用；而在近些年的研究中，新的有影響力的理論或模型未見發表［2］。1987年初，美國的朱經武等和中國科學院物理研究所的趙忠賢分別發現了超導轉變溫度Tc超過90 K的Y-Ba-Cu-O超導體［3］，這雖距離超導的實用又邁進了一步，但仍離室溫超導應用很遙遠，且進展緩慢。目前，二硼化鎂的制備和摻雜［4－5］，以及超導帶材的制備等應用研究［6－8］比較活躍。

雖然超導的臨界轉變溫度Tc不斷提高，但目前在高溫超導方面遇到的困難依然是巨大的［9］。科學界針對超導現象提出的幾十種唯象模型雖能解釋一些實驗現象，但除“BCS電-聲機制”外，其他各種交換作用的“激子機制”“雙極化子模型”“共振價鍵態機制（RVB）”以及“電子-負u中心模型”等，在用來解釋具體的超導體時，都會遇到許多問題。這說明人們目前對于高溫超導電性的認識在理論上還是初步的，需要進行深入探討。本文將對導體的電阻與超導態進行理論研究，并對超導現象進行分析。

1　導體的電阻效應分析

非超導態的導體導電是導體中自由電子定向移動的結果，而導體中產生電阻則是自由電子在定向移動的過程中與原子碰撞的結果。該碰撞過程可以看作是電子從該原子的無窮遠處的能級向低能級躍遷并輻射能量的過程，而躍遷到低能級的電子可能會在室溫下擺脫原子核的束縛而再次成為自由電子，繼續參與導電，并繼續與下一個原子碰撞輻射能量。圖1所示為導體產生電阻的微觀圖像。

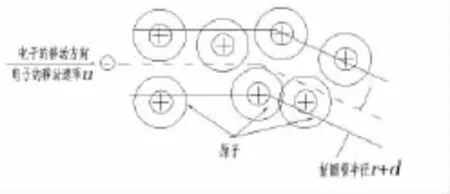
圖1　電子與原子碰撞示意圖

假設某導體在室溫下原子數密度為n，半徑為r，且每個原子貢獻s個自由電子，即電子數密度為sn，則該導體單位體積的電子數為Q=1·sn（以下討論均為單位體積的導體），電子在導體中定向移動的平均速率為u，電子直徑為2d，則由圖1可知，中心在半徑為（r+d）的折圓管內的原子均會與該單電子相碰撞，故單電子與導體原子的碰撞頻率為

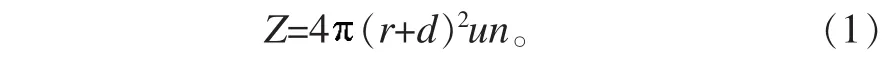
假設每一次電子與原子碰撞使原子輻射的能量都為hν，則單自由電子使原子輻射的功率為Pe=Zhν=（r+d）2unhν，導體中所有的自由電子使導體原子輻射的功率P=QPe=（r+d）2usn2hν。可見，影響材料電阻大小的因素僅為u。過大的u將會導致電子向更低能級躍遷，輻射出更高頻率的能量，使導體出現發光發熱的現象，而損失大量的電場能。若輻射的能量又被其他原子吸收，則該原子會產生振動，從而使導體產生熱效應。

2　導體電阻隨溫度的變化與導體電子的束縛態

假設在某導體中，原子價電子層電子擺脫原子核束縛所需要的最低能量為Eε，即最外層電子的活化自由能為Eε，則每個價電子擺脫原子核束縛成為自由電子的概率服從Boltzmann分布，即

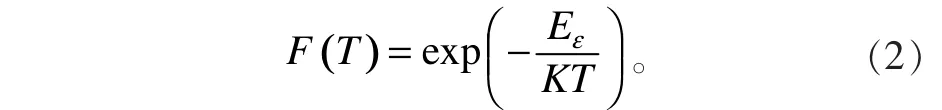
其中，T為熱力學溫度，F（T）為電子在T溫度下擺脫原子核束縛而成為自由電子的概率，K為Boltzmann常數。

由于束縛態的電子不參與碰撞，即束縛態電子對導體電阻效應沒有貢獻，這樣，根據以上分析與（2）式可得，在外電場不變的情況下，導體電阻隨溫度的變化關系，也即P和溫度的關系為P（T）=P·F（T），即

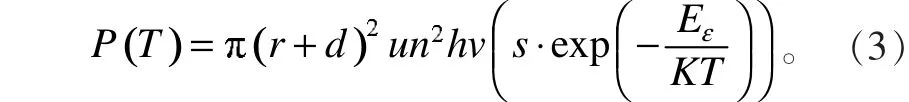
由以上分析可知，要使導體產生零電阻效應（即導體電阻幾乎為零），應使導體在某一溫度T范圍內有P（T）≈0，而此時應有F（T）≈0，即導體中原子最外層的電子基本都處于束縛狀態，導體中幾乎無自由電子與原子碰撞輻射能量。也就是說，超導態轉變的首要條件是導體中原子的最外層電子處于束縛態。

功率損耗P（T）也可以使導電材料原子的束縛態電子變為自由電子，產生的自由電子又可在電場作用下與原子碰撞并輻射功率E（T）。結合以上分析可知，E （T）應是P（T）的函數，即E（T）也是隨溫度變化的。總之，實際導體材料的電阻效應Q（T）主要是P（T）與E（T）的和，即

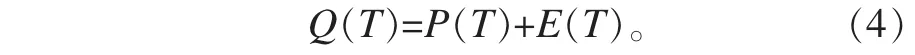
3　超導態微觀圖像及材料的超導態第一臨界轉變溫度

3.1Stark效應與超導微觀圖像

當導體處于超導態時，對超導體中導電電子的波函數的計算不具有一般性，這主要是因為能產生超導態的材料多種多樣，包括單質、化合物、合金等，每一種超導材料都對應一個不同的超導態電子的波函數。雖然如此，但是每一種超導材料都遵循和對應著相同的超導原理以及一個基本的微觀超導圖像，比如，當氫原子處于基態時，若沿水平方向上加上均勻電場ξ，則氫原子基態電子的運動規律（Stark效應）是，在無外加電場時，氫原子基態波函數為其中為Bohr半徑，零級能量為，由參考文獻［10］知且視外加電場為微擾，經過計算［10］可得氫原子基態波函數的極化率為，即氫原子基態波函數在電場中產生了偏離（如圖2）。此效應具有一般性，即其他原子也會產生類似的效應。

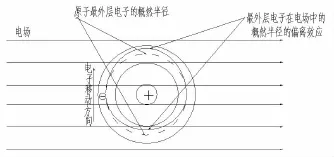
圖2　氫原子概然半徑偏離示意圖

上述模型中的“原子”，不僅可以表示單質原子，也可以推廣為組成超導體的符合布洛赫周期勢場的晶體。為了分析方便，以下分析均以“原子”模型為研究對象。

兩個價電子層軌域相干的原子處在沿水平方向上的均勻電場ξ中又是怎樣的一種物理圖像呢？價電子波函數在電場中出現偏離，會使價電子在原子軌域做定向移動，且無能量損耗，將該圖像推廣至整個導體，便是導體在束縛態溫度下的超導微觀圖像，如圖3所示。

可見，所謂的超導態就是電子處在束縛態并在電場的作用下在價電子軌域做定向移動的效應，且該定向運動過程沒有碰撞等能量損耗。

3.2超導材料的第一臨界轉變溫度

由2可知，P（T）≈0時表示材料的自由電子轉變為束縛態電子，但因為滿足P（T）≈0的P的值很多，所以材料的導電電子轉變為束縛態電子并不一定表示材料轉變成了超導體。假設P（T）的取值PN滿足數值大小約等于零的條件，即P（T）=PN≈0，但此時材料可能并沒有進入超導態。這是因為，盡管PN取值很小，但導電材料依然可以產生一定的能量損耗，且這些能量損耗能使該導電材料中的束縛態電子變為自由電子，該部分自由電子將繼續在電場作用下與材料原子碰撞并輻射能量E（T），這些能量與P（T）的累加又破壞了其他電子的束縛態，從而引發對材料束縛態電子的“雪崩”式破壞，即該超導材料在PN取值下不能形成穩定的超導態。

圖3　電子超導態微觀輸運圖像（一維）

因此，P（T）的取值必須進行嚴格的限制，假使在允許范圍內，P（T）的取值最大不超過PS時表示材料進入超導態，且此時E（T）=0可以忽略不計，即導電材料產生的能量損耗幾乎不會對該材料的束縛態電子產生影響，則在超導態時，（4）式可變為

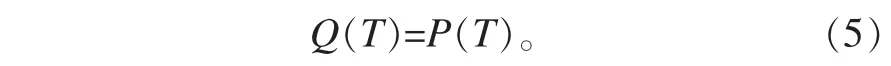
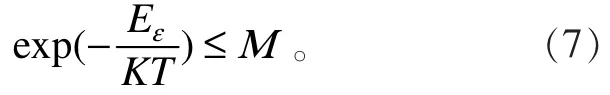
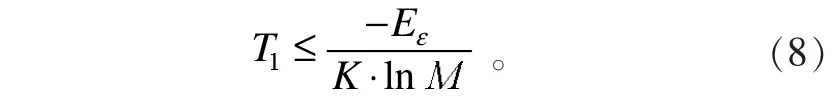
M為一受PS和具體材料性質影響的無量綱數，且M∈（0，1），因而ln M也為一受具體材料影響的無量綱數。當（8）式取等號時，T1即為超導材料的第一臨界轉變溫度。

在超導體中，處于原子軌域中的束縛態電子遵守泡利不相容原理，即在電子層軌域的束縛態電子最多有兩個，且這兩個電子必須是自旋相反的。當有外界強電場或磁場破壞其中一個電子的束縛態，那么另一個電子擺脫束縛態成為自由電子的概率服從如（2）式的Boltzmann分布。這也是筆者認為實驗觀測發現磁通量子化中電子是“成對”的原因。

3.3電場對超導的影響

當導體處于超導態時，沿水平方向加均勻電場ξ，當電子由價電子層趨近原子核方向時，外加電場對電子做正功，使該價電子的活化自由能增加

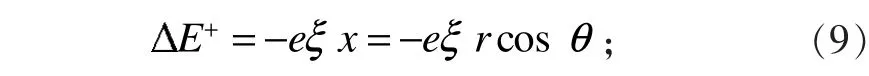
而當價電子遠離原子核時，外加電場對價電子做負功，使該價電子的活化自由能減少

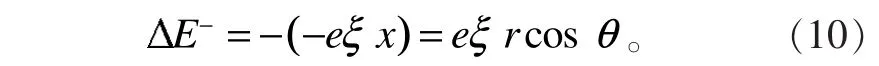
從（9）式與（10）式可知，電場對超導體電子做功之和ΔE為0，即ΔE=ΔE++ΔE-=0。

電場使價電子的活化自由能增加，將維護電子的束縛態；而電場使該電子的活化自由能減小，將破壞電子的束縛態，使束縛態電子轉變為自由電子，這將降低超導轉變的臨界轉變溫度。取θ=0，由（8）式得

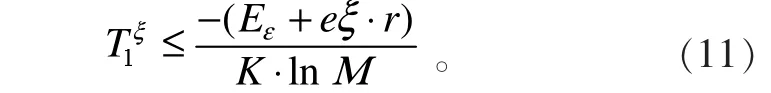
另外，關于磁場對超導的影響分析與對超導施加電場的分析類似，不再贅述。

4　超導態第二臨界轉變溫度

由以上論述可知，超導態中原子之間的軌域相干也是導體轉變至超導態的必要條件，而原子的熱振動會破壞原子間的軌域相干。

4.1溫度對原子之間軌域相干的破壞

設當溫度T無限趨于絕對零度時，導體中兩原子間的相干度為l（即兩相鄰原子間的最大重合度為l，如圖3所示），原子間恢復力系數為β，且原子的熱運動符合Maxwell-Boltzmann速率分布律，即

其中，m為原子的質量，v為原子的熱運動速率。

考慮到熱運動速率大的原子也會對原子間相干度有更大的影響和破壞作用，故在考慮原子熱運動時使用原子熱運動的均方根速率vrms，即

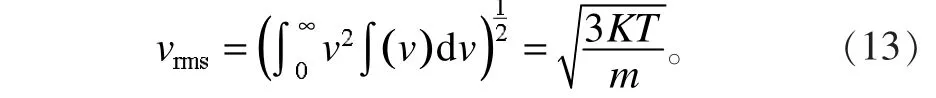
要保證兩個原子之間的軌域相干，則必須使原子在某一溫度T2時，原子熱運動的最大振幅ΔC不大于軌域相干度的一半，即

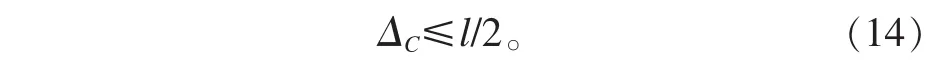
由于恢復力系數β的存在，原子的熱運動可看作是原子在平衡位置的簡諧振動，又考慮到原子的每個振動方向上總相當于兩個原子相互為相干態（如圖3所示），故有

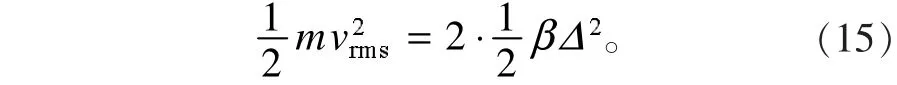
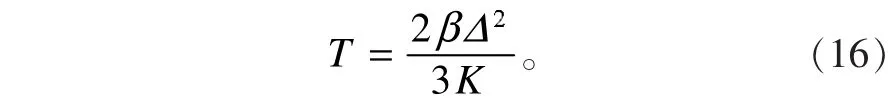
由（16）式和（14）式可得該超導體的超導態第二溫度

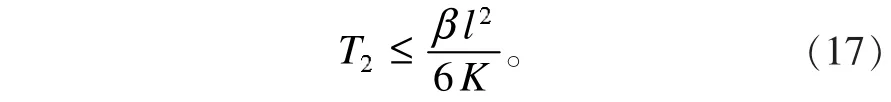
導體材料轉變為超導材料還須滿足（17）式的溫度限制，即必須滿足轉變溫度Tc=min（T1，T2）。

4.2外應力對超導第二臨界轉變溫度的影響

當某一超導材料中的價電子處于束縛態時，若對該材料沿水平方向施加一外應力F，則該固體原子之間沿水平方向上的相干度將增加δF，即在外應力F的作用下，固體原子之間沿水平方向的相干度為lF=l+δF。

在維持材料原子相干態的情況下，原子熱運動的最大振幅ΔC在F的作用下可增加到ΔFC，結合（14）式可得

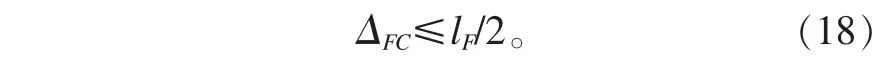
這將增加超導體的超導第二臨界轉變溫度，根據（16）式和（18）式可得在F的作用下，超導第二臨界轉變溫度為

可見，在導體電子為束縛態條件下，對超導體施加外應力將會顯著提高超導臨界轉變溫度［9］，但通過該方法也僅能使超導臨界轉變溫度提高到超導材料的第一臨界轉變溫度。

5　本文的不同認識和理解

5.1導體材料原子的熱振動對電阻效應的影響

由4中的分析可知，材料原子（或材料晶胞）振動的幅度Δ一般小于等于其原子間相干度l，而原子間相干度一定遠遠小于其原子半徑r，即

材料原子（或材料晶胞）的振動幅度Δ相當于增加了電子與原子的有效碰撞半徑，即增加了原子的有效碰撞面積，也即增加了電子與原子的碰撞頻率。由（1）式可得

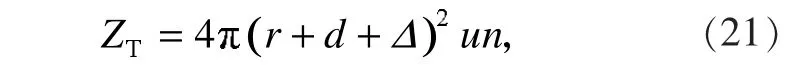
則

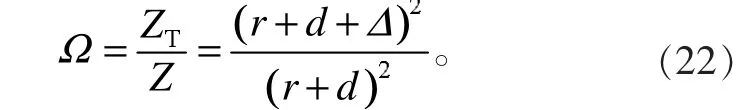
又根據（20）式知

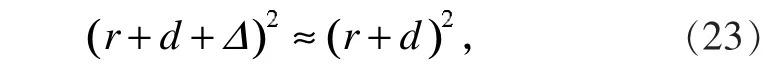
即

可見，材料原子的熱振動效應基本不會對電子與原子的碰撞頻率構成影響，即導體材料原子的熱振動對電阻效應的影響可以忽略。

使材料原子（或材料晶胞）振動的幅度Δ等于其原子間相干度l的溫度為該材料的固-液相變溫度，在此溫度下，材料原子間的相干度極小，原子在材料中具有流動性。根據（16）式可知一般凝聚體的固-液相變溫度為

一般導體溫度都會小于其固-液相變點的溫度，即實際材料原子（或材料晶胞）振動的幅度Δ遠小于其原子間相干度l。導體材料原子的熱振動對電阻效應貢獻是極小的。

另外，導體材料的雜質與缺陷也是影響電阻效應的重要因素，但考慮到本文所討論的材料為理想純凈材料，即沒有雜質與缺陷的材料，該類理想材料的電阻效應主要由P（T）與E（T）構成，且當超導材料處于超導溫度范圍內時，該超導體的電阻效應是P（T）貢獻的。因此，在超導轉變中，材料的電阻會出現一個“驟然變零”效應，即材料在超導轉變時電阻效應E（T）突然消失。

目前所制備的超導材料已經非常接近該理想導體材料，其雜質和缺陷引起的電阻效應基本可以忽略。

5.2對具有高超導轉變溫度陶瓷材料的解釋

以前被稱為絕緣體的陶瓷材料，有很多已經被發現是超導材料。筆者對此現象的解釋是：這些陶瓷材料在較高溫度下便滿足前文所述的所謂超導第一臨界溫度，即超導陶瓷的電子處于束縛態，當溫度繼續降低時，陶瓷材料滿足超導第二臨界溫度，即軌域相干。因為陶瓷類材料氧化物間的作用力比較小，即所謂原子間相干度l較小（物理特性表現為該類材料的延展性較差等），所以，這類材料的超導第一臨界溫度往往大于其超導第二臨界溫度，一個具體的表現是：在對這類超導材料施加外應力時往往能提高其超導第二臨界溫度。可見，束縛態是材料超導轉變的基本條件之一。

6　結論

根據本文中所建立的一般導體材料中電子與原子碰撞的物理模型及材料電子在超導態下的微觀輸運模型可得如下結論。

（1）導體產生的電阻效應是自由電子在做定向移動時與原子碰撞并損失能量的結果。若輻射的能量被其他原子吸收，會使該原子產生熱運動而導致導體發熱。

（2）材料向超導體轉變的條件之一是其原子的最外層電子處于束縛態。超導體電子輸運是基于原子軌域電子在電場中的Stark效應，電場對超導轉變溫度也有影響。

（3）原子的熱振動對超導態有破壞作用，即熱振動會對超導體臨界轉變溫度產生限制，不過可以通過對超導體施加外應力來抑制原子的熱振動對超導態的破壞，這表現為在對超導體施加外應力時，超導轉變臨界溫度顯著提高。

［1］BARDEEN J，COOPER L N，SCHRIEFFER J R.Theory of Superconductivity［J］.Physical Review，1957（5）: 1175-1194.

［2］鄒壯輝，周志敏，王明光，等.本征超導態的理論分析和計算超導臨界溫度Tc新方法［J］.2008（7）：1317-1322.

［3］張彥生，田興，李曉麗，等.高轉變溫度超導材料YBa2Cu3O9-y的研究［J］.大連鐵道學院學報，1987（2）：101-102.

［4］孔祥東，戴倩，韓立，等.電子束退火制備二硼化鎂超導薄膜的可行性研究［J］.真空科學與技術學報，2012（8）：758-762.

［5］王醒東.新型MgB2超導材料的制備及應用［J］.廣州化工，2013（11）：47-48.

［6］葉帥，索紅莉，劉敏，等.改進YBCO薄膜高場性能的研究進展［J］.低溫物理學報，2008（1）：23-28．

［7］徐琬琛，柏躍玲，方建慧，等.MOD法制備YBCO超導薄膜的研究進展［J］.材料導報，2013（23）：37-41.

［8］王醒東.REBCO高溫超導帶材緩沖層的結構及制備方法［J］.電工科技，2014（3）：36-39.

［9］韓汝珊.高溫超導機制研究近期重要進展［J］.物理，2004，33（12）：890-898.

［10］曾謹言.量子力學：卷1［M］.北京：科學出版社，2007：361-362.

［11］梁芳營，劉洪，李英駿.高溫超導的壓力效應研究［J］.物理學報，2006（7）：3683-3687.

【責任編輯梅欣麗】

Resistance Effect of Conductors and the Theory of Superconductivity

WU Yuan
（College of Science and Technology，Beijing Humanities University，Beijing 101300，China）

From the analysis of the origin of conductor resistance，it was known that the first transition temperature of a superconductor was such a temperature at which all the electrons in the conductor should be in a bound state.Microscopic transport images of electrons in superconducting state were described by using the Stark effect of atoms'bound electrons in an electric field，and a mathematical expression was then deduced for the first superconducting state transition temperature.The thermal vibration （phonon）of superconductor atoms had a destructive effect on the inter-atom orbital coherence，in other words，the thermal vibration of atoms was another factor restricting the transitional critical temperature of superconducting state.The second superconducting state transition temperature，which was related to atomic thermal vibration，was found by analysis.This temperature reflected the restrictive effect of atomic thermal vibration on superconducting state transition.

superconducting transition temperature；coherence；phonon；bound state

O511+.2

A

2095-7726（2016）03-0015-05

2015-11-07

武圓（1991-），男，河南永城人，研究方向：理論物理。