讓數學靈動起來

顏榮林 田海琪

【摘 要】“九宮圖”是一個簡易的數學模型，卻蘊含著大量的數學規律。教師要想在探究“九宮圖”的各種內在數學規律的基礎上，充分開發“九宮圖”的教育價值，就要對九宮圖的文化背景、九宮圖的不同填法、“九宮圖”的數字規律等進行深入的分析，從而提出教學設想。

【關鍵詞】九宮圖 教學價值

“越是簡單的知識，越能體現數學的本源。”九宮圖就是這樣的一個例子。在3×3的九個方格中，分別填入1至9這九個數。這是一個十分簡單的數學問題，簡單到只要以“20以內的加法”作為基礎，就可以解決這個數學問題（如右圖）。但是，卻賦予它神話的色彩，下面讓我們慢慢走進“九宮圖”的世界。

一、九宮圖的文化背景分析

相傳，在夏禹時代，洛水中曾出現過一只大的神龜，它的背殼上有個圖（如左下圖），人們把這個圖稱作“洛書”。據說，這個圖中蘊含了世間萬物的變化規律， “洛書”為當時的首領大禹所得，他從中悟出了治理天下的道理。

“洛書”比較形象的稱法是“九宮圖”或“縱橫圖”，它的神奇特點吸引了無數人對它癡迷。從我國古代的“河出圖，洛出書，圣人則之”的傳說起，系統研究九宮圖的第一人，是我國古代數學家——楊輝。

在國外，公元1300年被希臘數學家莫斯切普羅所推廣，成為許多數學家傾注精力進行研究的一個數學題材。

九宮圖中的原理連小學生都很容易理解，但它的內涵卻是十分豐富的，它通過數字間的周轉變化，數與形的和諧統一，局部與整體的全息對應，描繪出一個生動的宇宙演化的數學模型。它蘊含著大量的數學規律，“線線諸數合幻和、縱橫巧合聯四方、和差積方都巧等、三角方圓均有律”，它與算術、數論、幻方、代數幾何、矩陣、趣味數學等都有聯系。古今中外，不知多少學者著書立說，對九宮圖進行深入的探索。

從上面的闡述中，感受到了“九宮圖”所特有的文化內涵，從它“現世”的那一刻起，就注定成為一個融數理與神話為一體的數理哲學的化身。因此，在引入“九宮圖”時，如果我們能創設情境，恰當地闡述“九宮圖”的文化背景，可以激發學生對“九宮圖”進行深入研究的興趣。為后面研究或了解“九宮圖”的各種不同的填法積累情感的基礎。

二、九宮圖的填寫方法分析

九宮圖的填法，如果用算術法湊數，可以用“羅列數組，對號入座”的方法很快地填出。但是，人們在此基礎上，還創造出了許多口訣，根據口訣，可以按部就班地填出九宮圖，增強填寫“九宮圖”的趣味性。下面我們列舉幾種適合小學生填寫與了解的方法，并簡要說明大致的教學設想。

（一）羅列數組，對號入座

這是最常用的構造九宮圖的方法。

我們知道，把1至9這九個數填入“九宮圖”，由于9個數的總和為45，每橫行、每豎列、每橫行和每斜行的三個數的和均相等，所以這樣的每三個數的和都應該是15，也就是說從1至9中選出三個數，至少需要組成8組不完全相同的和為15的數組。經過試驗有且只有8組，分別是（1，5，9，）（2，5，8）（3，5，7）（4，5，6）（2，4，9）（2，6，7）（3，4，8） （1，6，8）。

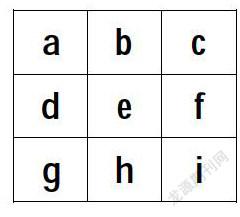
再觀察右邊的九宮圖，寫出以上8組和時，中間e的位置上的數被用到了4次，角上a，c，g，i的位置上的數被用到了3次，而邊上b，d，f，h的位置上的數只被用到了2次。

按上面的規律，把8組數中各個數出現的次數做一個統計，可以發現“5”被用了4次，“2，4，6，8”各被用了3次，“1，3，5，7”各被用了2次。經過試驗自然就可以把各個數“對號入座”了。

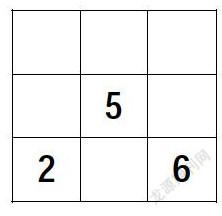
從上面的敘述中，可以設想到，如果只給出要求，學生按要求把1至9這九個數填入九個方格中，學生首先會進行嘗試，當出現錯誤時，會不斷地調整，這是最原始的嘗試法。之后，再引導學生反思填寫要求，逐步發現上面敘述的有序的填寫思路。這就是數學思考的力量。這樣的一個過程適合三年級時組織學生填寫。而對于一、二年級的學生則可以先填其中部分數，讓學生根據規則，填寫出滿足要求的其他位置上的數。如請補全右面的“九宮圖”。

（二）歸納口訣，記憶填數

用上面的填法，固然可以填寫九宮圖，但是需要一個較長的過程。因此，還可以編寫出填寫的口訣。這些口訣又可以分為兩類，一類是直接填數法，一類是表述過程法。

1.直接填數法

直接填數法就是依據口訣，可以依次直接填寫出各個位置上的數。最有名的是：

戴九履一，左三右七，二四為肩，六八是足。

上面的口訣，分明就是一只烏龜的造型，如右圖。

下面的口訣則是根據奇數與偶數不同位置特點編寫而成的。

九數從小排到大，中間數字中間填，四角填上偶數項，余下四數再補全。

根據上面的口訣，可以按如下的圖示填寫。

這給我們提供了很好的教學思路：在學生按“羅列數組，對號入座”的方法填寫出“九宮圖”后，請學生閱讀上面的兩句口訣，說一說這兩句口訣的意思及編寫的思路。然后請學生再獨立找一找“九宮圖”中各個數的其他特征，自己來創作一句填數口訣。

2.表述過程法

用直接填數的口訣雖然形象生動，但是如果把它作為真正的填數方法，可能要增加學生的記憶負擔。所以人們又創作出了另一種口訣，描述的是如何從最簡單的數的排列，通過最簡便的數的位置移動，實現填寫九宮圖的目的。

下面介紹的就是楊輝創造的一種填數口訣：

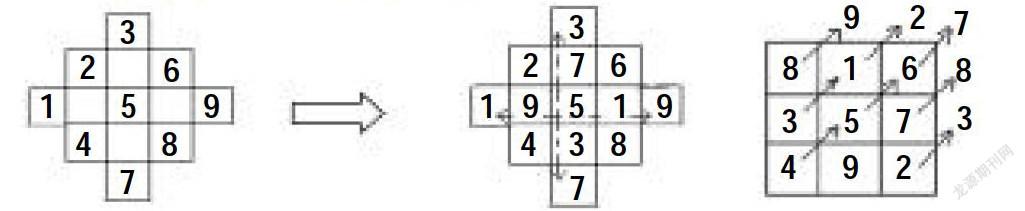
九數斜排，上下對易，左右互換。

讀完上面的口訣，再看下面的兩個圖示，是否學會了“九宮圖”的快速填法了？

在國外也有類似的口訣， “羅伯”口訣是其中有名的。

一填首行正中央，依次斜上莫要忘，

上出下填右出左，若是重了填下方。

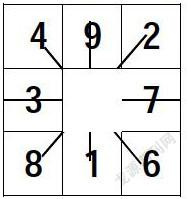
右邊的圖示反映了按上面的口訣填數的過程。

根據口訣，只要找到“1”的位置，然后按規則從小到大填入其余各數的位置。

上面的這些填法，如何成為教學資源？我們設計了兩種方案。

第一種方案是逐步滲透法。在一年級的教學中，根據學生的計算能力，做一些填數游戲，二年級再請學生按“羅列數組，對號入座”的方法填數，到了三年級，再請學生欣賞與研究口訣填數。

第二種方案是主題教學法。在三年級或者四年級時，組織一堂數學活動課，把以上一、二、三年級的教學內容串聯成一堂活動課，讓學生整體感受“九宮圖”填寫的內在魅力。

三、九宮圖的內在規律分析

從上面的填寫法的分析中，我們感受到了數學家對于“九宮圖”的喜歡，他們不滿足于常規的填法，創造出了許多口訣，體現了數學家的創造精神。但是，“九宮圖”真正吸引人們，尤其是數學家的研究興趣的，并不僅僅是它的數學文化背景或它的填法創造，更為重要的是“九宮圖”——這個只有9個數構建而成的數學模型中所蘊含著的數學規律。筆者收集了其中一些淺顯易懂的規律，力圖讓它們成為教學資源。

（一）“田—口=15”

“九宮圖”中的任何一個“田”格中的4數之和，減去與此“田”格不同行不同列的另一格之數，必等于15。如（2+9+7+5）-8=15，（7+5+6+1）-4=15。

（二）相等數對

把“九宮圖”的中心格5抹去（如左圖）以后，經過中心格的任一條線上的兩數和均是10。其實這種相等的數對處處可見：我們隨意壓住“九宮圖”中的一格，那么與這格相交的各線，所剩的兩數的和全相等。就如我們提起一個正方形網片一樣，無論我們從哪個角上提起，從這個角向三個方向看去，所看到每條線上的兩數之和都相等。

（三）遞增和

“九宮圖”中對稱的兩行或兩列，將每行（列）各數依次乘一個等差數列的各項，各項積之和必相等。例如

2×1+9×2+4×3=6×1+1×2+8×3=32。

2×5+9×8+4×11=6×5+1×8+8×11=126。

4×11+3×21+8×31=2×11+7×21+6×31=355。

（四）平方和相等性

“九宮圖”的第一、三行或者第一、三列所含的數的平方和相等，即42+92+22=82+12+62=101，42+32+82=22+72+62=89。

此外過中心4線上各數的平方和也有規律，請看：（22+52+82）+（42+52+62）+10=（72+52+32）+（92+52+12）-10=180。

（五）循環積和

“九宮圖”中第一、三行或第一、三列，順次兩數相乘，其和必相等，即

2×9+9×4+4×2=6×1+1×8+6×8。

4×3+3×8+8×4=2×7+7×6+6×2。

（六）對稱積和

在對稱的兩行或兩列中，一條線上，兩端兩數之積的2倍，與中間一數的平方之和相等，例如

（2×4）×2+92=（6×8）×2+12=97。

（6×2）×2+72=（8×4）×2+32=73。

以上只是筆者收集到的關于“九宮圖”規律的一小部分。顯然，要把它們轉化成課程資源，需要教師進行創造性的開發。

首先，把這些規律按發現的難度進行分類。如上面的六個規律，由易到難，最簡單的是“相等數對”的規律，最難的當數“對稱積和”。

對于這些規律，在教師的引導下進行自主發現。在這個過程中，如果學生有其他的新發現，同樣給予肯定。如要求學生找“相等數對”時，有一位學生說，他還發現了“角上的數是相對的兩個肩上數的和的一半”，并舉例子：8=（7+9）÷2。同時，在找到“相等數對”后，教師也可以進一步追問與引導，讓學生從中發現新的規律，如可以從“相等數對”中衍生出：角上四個數的和等于邊上四個數的和。

其次，把這些規律按與教材知識的匹配程度分，具體安排在各個不同的年級，引導學生有不同的發現。

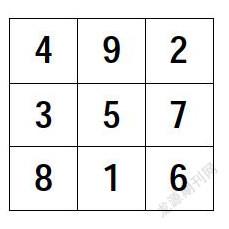
如在學習了多位數加法之后，教師請學生按下面的要求計算：計算順寫的三個三位數的和與逆寫的三個三位數的和，進而總結出：順寫的三個三位數的和等于逆寫的三個三位數的和。如 816+357+492=618+753+294。

進而追問：為什么會有這樣的規律？知道了為什么后，再請學生計算豎著的順寫與逆寫的情況下三個數的和是否相等。

上面的活動，利用學生新近學習的計算方法來探究“九宮圖”中的新規律。既有利于提高學生的計算技能，同時又豐富了對“九宮圖”規律的新認識，激發了學生的學習興趣。

總之，對作為教學資源的“九宮圖”規律的探究，并不是只為了探究規律而組織活動，它完全可以融合到我們平時的計算教學中，為計算教學平添了一道人文風景。

（浙江省杭州市蕭山區所前二小 311200浙江省杭州市蕭山區北干小學 311200）