層次分析的慣導/重力匹配導航系統性能評估方法*
陳 晶, 董銘濤, 程建華
(1.海軍裝備研究院 艦船所,北京 100086; 2.哈爾濱工程大學 自動化學院,黑龍江 哈爾濱 150001)
?
層次分析的慣導/重力匹配導航系統性能評估方法*
陳晶1, 董銘濤2, 程建華2
(1.海軍裝備研究院 艦船所,北京 100086; 2.哈爾濱工程大學 自動化學院,黑龍江 哈爾濱 150001)
提出了基于層析分析法的系統精度性能評估方法。在分析慣導/重力匹配導航核心誤差要素的基礎上,建立了基于多層的系統結構體系描述;設計閾值和遍歷相結合的系統性能分值確定方法,解決了傳統層析分析法的權重模型描述和權重確定客觀性問題。實例表明:精度性能評估方法是有效的,該方法為評估慣導/重力匹配導航系統性能,進而實現系統性能優化提供了參考,具有一定現實意義。
慣導/重力匹配導航; 性能評估; 層次分析法; 精度; 閾值
0 引 言
慣導/重力匹配導航系統,是通過地球重力場匹配的位置信息與慣性導航系統(簡稱慣導系統)位置信息的最優融合,進而實現高精度自主導航的一種組合導航系統[1,2]。由于能實現慣導水下校準,特別適合潛艇、各類潛器等水下航行器應用[3,4]。
作為慣導/重力匹配導航的核心要素(子系統),慣導系統精度、重力儀精度、重力圖分辨率、匹配算法、適配區和信號估計方法直接影響了最終的信息融合精度[3~6]。不同精度的子系統會導致最終的組合導航精度差別很大。因此,從系統方案設計、驗證角度,對慣導/重力匹配導航系統開展性能評估,定量確定各子系統對信息融合精度影響程度,將為方案驗證和優化提供重要的技術支撐。
層次分析法(AHP)、灰關聯法等性能評估方法,在組合導航領域已得到了廣泛的應用[7,8]。其中,層次分析法具有對多層次系統有很好的使用性、確定的權重也較為客觀的特點,非常適合于具有層次特點系統性能評估。王敏建立了基于層次分析法的組合導航系統性能評估方法。但由于確定判斷矩陣僅參考專家的經驗,作者沒有解決權重的客觀性問題。
本文針對慣導/重力匹配導航這一主流水下用組合導航系統,開展基于層析分析法的性能評估方法研究,利用遍歷法思想仿真確定仿真實驗數據,通過引入閾值法解決求取權重時僅依靠專家經驗導致破壞客觀性問題,進而實現系統精度性能的定量評估。
1 慣導/重力匹配導航系統分析
慣導/重力匹配導航系統原理如圖1所示。
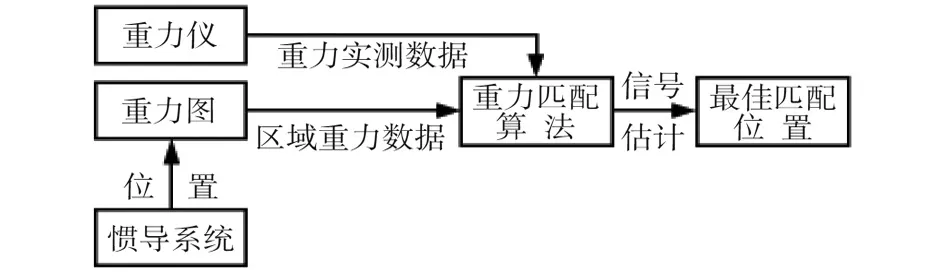
圖1 慣導/重力匹配導航系統原理
1)慣導系統為重力匹配導航提供參考坐標。重力匹配需要根據慣導系統各個時刻的粗略指示位置從重力圖上提取參考重力數據。當慣導系統誤差過大時,會導致系統無法在適配區中匹配真實位置,進而導致匹配失敗[9]。
2)重力儀系統為重力匹配導航提供重力測量值。當重力儀量測誤差過大時,也會產生實時測量的粗略重力數據與重力圖中數據無法匹配的問題,導致匹配失敗。
3)重力基準圖為重力匹配導航提供匹配重力數據。重力匹配導航必須建立精度和密度均滿足要求的重力圖;否則,就不可能實現運載體的精確定位。
4)適配區是重力匹配過程中必不可少的條件。適配區重力場特征越明顯越是有利于重力匹配,因此,適配區一般需要選擇在重力場特征獨特的區域中進行,以提高重力匹配導航精度。
5)重力匹配算法是重力匹配導航的關鍵技術。重力匹配算法通過實時測量重力值與存儲在重力圖中的重力值進行匹配,經信號估計后求得最佳匹配位置。
6)系統完成位置匹配后,還需要與慣導系統的位置進行信息融合,需要信號估計方法具有從這些含有噪聲、誤差的數據中提取或恢復精確信息的能力。
2 系統評估體系與評估方法設計
2.1系統層析結構體系描述
由前述分析可知,慣導系統精度、重力儀系統精度、重力圖分辨率以及適配區精度之間相互獨立,而匹配算法與信號估計是建立在前者的基礎之上,同時,信號估計是在重力匹配完成之后才能實現。本文建立慣導/重力匹配導航系統層次結構如圖2所示。
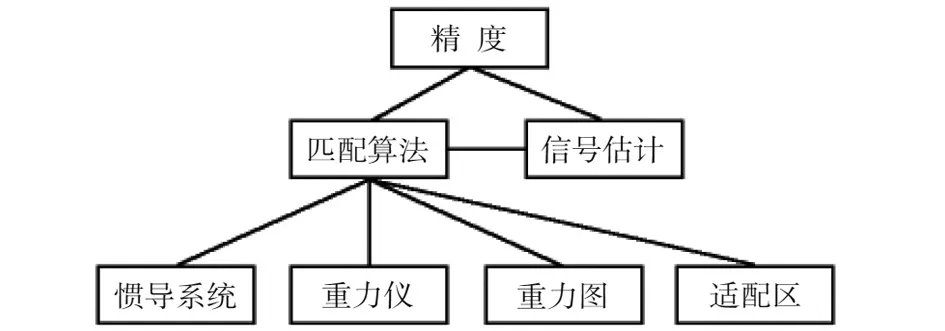
圖2 慣導/重力匹配導航系統層次結構圖
2.2系統性能評估方法
利用式(1)定量地確定系統的性能分值,即
(1)
式中ci,di為各子系統性能分值;xi,yi為對應子系統指標的權重;X為系統性能分值。i =1,2,3,4,j =1,2,l =1,m=2。
3 系統權重模型的改進
慣導/重力匹配導航系統指標體系中需要根據指標對融合精度的影響確定其權重的大小。層次分析法是多層次多指標系統確定權重的有效工具,然而傳統的層次分析法構建判斷矩陣方法是由專家對每一層元素兩兩比較,參考應用最為廣泛的1~9標度法(表1)而得到。該方法能夠充分利用專家的經驗,但是人為主觀性因素會導致權重的主觀性偏大,從而破壞了權重的客觀性。

表1 判斷矩陣標度方法及含義
本文引入閾值法[10]。
為考量各子系統精度對組合導航系統信息融合精度的影響,此處將閾值選為最終定位精度值
(2)
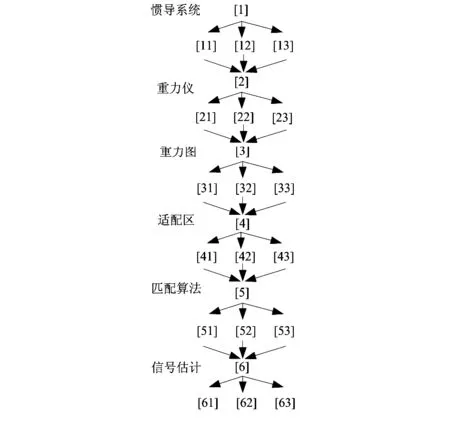
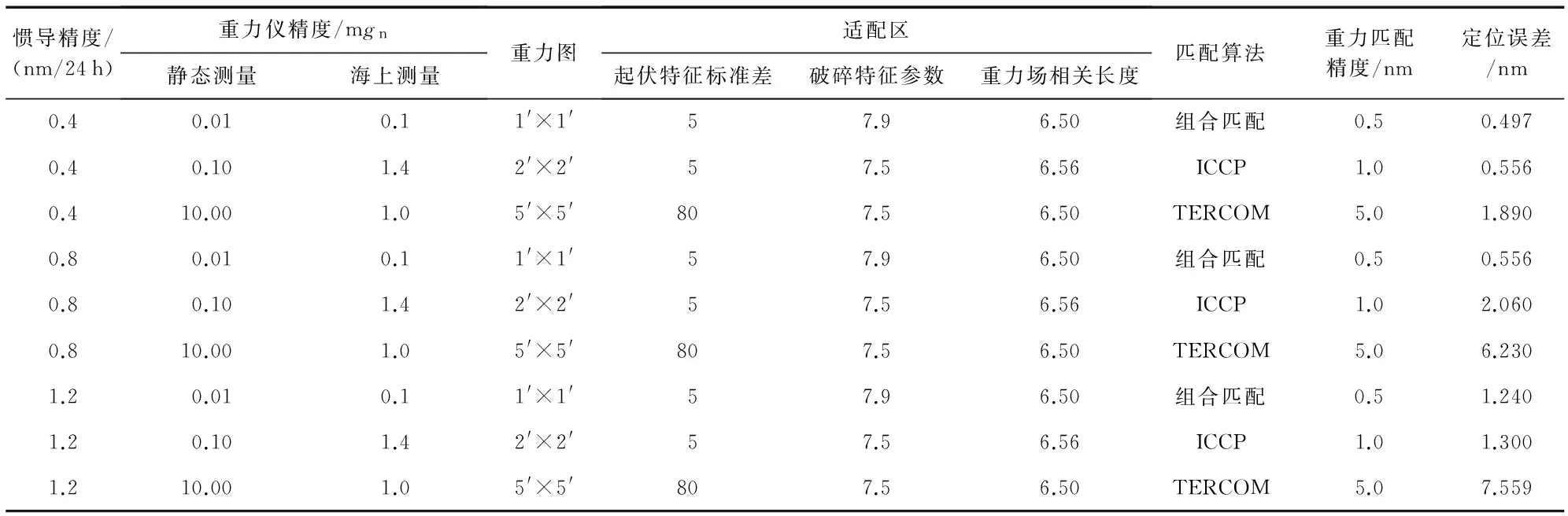
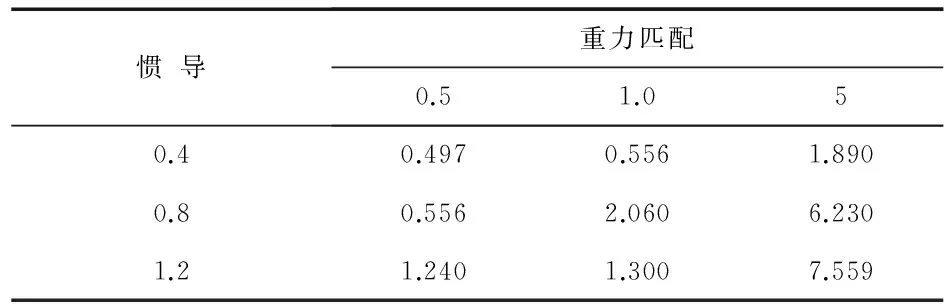
式中i=1…6,zi為系統信息融合精度值,ai為各子系統精度值,bi為指標標準值。考慮到精度指標越小越好,并且判斷矩陣元素取值為1~9,故對標準值做如下處理:若0 為了更加全面的分析各子系統對系統信息融合精度的影響,設計遍歷法[11]對系統誤差模型遍歷。慣導/重力匹配導航系統遍歷法原理圖如圖3所示。 圖3中,[1],[2],[3],…,[6]依次為慣導系統、重力儀系統、重力圖、適配區以及信號估計方法,[11],[12],[13],…,[61],[62],[63]依次表示各子系統性能指標在精度范圍內的取值。 設F([1],[2],[3],…,[6])是關于各子系統性能指標函數,此時訪問就是對各子系統性能指標精度值以誤差方程的方式進行處理。借助Matlab[12]軟件可實現各子系統性能指標精度值遍歷慣導/重力匹配導航系統誤差模型,從而得到慣導/重力匹配導航系統定位精度值。 圖3 慣導/重力匹配導航系統遍歷法原理 5.1仿真實驗 初始位置設置為北緯44.754 5°,東經111.760 8°;為了減少厄特弗斯效應的影響,仿真軌跡設置為由北向南行駛,速度為5m/s。對于慣導系統,選用三種精度導航系統為0.4,0.8,1.2nm/24h。重力基準圖由海洋船測資料繪制得到。經過9h的組合匹配得到結果。利用卡爾曼濾波方法進行信號估計。基于遍歷法的慣導/重力匹配系統的仿真條件如表2所示,不同精度下的慣導/重力匹配系統仿真數據如圖4所示,總結圖中結果如表3所示。 說明:組合匹配方法首先利用TERCOM方法完成粗匹配,然后利用ICCP算法實施精匹配。 表2 仿真條件 圖4 不同仿真條件下的仿真結果 慣導重力匹配0.51.050.40.4970.5561.8900.80.5562.0606.2301.21.2401.3007.559 對系統精度劃分指標等級,如表4所示。 表4 精度等級/nm 5.2實際算例 5.2.1運用層次分析法確定權重 判斷矩陣指標順序的選擇并沒有明確的規定。本文選擇指標順序:慣性導航系統,重力儀系統,重力圖系統,適配區,匹配算法,信號估計方法。 由仿真實驗數據,得出第三層判斷矩陣為 (3) 采用特征值法求解A1W1=λmax1W1,利用Matlab可得,λmax1=4.081 3,W1=[0.636,0.130,0.173,0.061]T。 第二層判斷矩陣為 (4) 采用特征值法求解A2W2=λmax2W2可得,λmax2=2,W2=[0.667,0.333]T。 大體上來說,根據權重矩陣可知,慣導系統在整個慣導/重力匹配系統中占據很大的比例,也是影響系統定位精度的主要因素。盡管重力圖指標占據很小的權重比例,但是也會影響最終的精度,是提高慣導/重力匹配自主導航系統定位精度不可或缺的重要因素。通過第二層性能指標層權重矩陣可以看出,匹配算法相比信號估計方法對系統的定位精度的影響更大。 5.2.2定量確定系統的性能分值 假定慣導/重力匹配導航系統的5個指標的量化評分結果如表5所示。這里為簡化匹配算法對信號估計方法的影響,單獨量化信號估計指標(滿分為100分)。 表5 關鍵要素的量化評分 為了使評估結果更加直觀、簡潔,這里規定評估結果等級和對應的分數。如表6所示。 根據式(2),得出慣導/重力匹配導航系統精度性能總值為82.717,性能良好。 表6 評估結果等級 本文基于遍歷法開展慣導/重力匹配導航系統仿真實驗;引入閾值法改進判斷矩陣確定方法,使判斷矩陣的確定更加客觀,彌補了僅靠專家經驗的缺點;利用層次分析法確定慣導/重力匹配導航系統的權重,最終定量的得出系統的性能分值。該方法為評估慣導/重力匹配導航系統的定位精度性能提供了依據,具有一定的現實意義。 [1]Lowreys JA III,Shellenbarger J C.Passive navigation using inertial navigation sensors and maps[J].Naval Engineers Journal,1997,109:245-249. [2]Welker T C,Pachter M,Huffman R E.Gravity gradiometer integrated inertial navigation[C]∥2013 European Control Conference(ECC),2013:846-851. [3]徐遵義,晏磊,寧書年,等.海洋重力助導航的研究現狀與發展[J].地球物理學進展,2007(1):104-111. [4]袁書明,孫楓,劉光軍,等.重力圖形匹配技術在水下導航中的應用[J].慣性技術學報,2004(2):14-18. [5]彭富清.海洋重力輔助導航方法及應用[D].鄭州:解放軍信息工程大學,2009. [6]程力.重力輔助慣性導航系統匹配方法研究[D].南京:東南大學,2007. [7]王敏.組合導航系統性能評估與試驗設計[D].哈爾濱:哈爾濱工程大學,2011. [8]夏衛星,楊曉東,王旺,等.基于灰關聯的INS/GPS組合導航系統濾波效能評估[J].彈箭與制導學報,2012(4):41-44,48. [9]蔡體菁,陳鑫巍.基于層次分析法的重力匹配區域選擇準則[J].中國慣性技術學報,2013(1):93-96. [10] 馬亞龍.評估理論和評估方法及其軍事應用[M].北京:國防工業出版社,2013:32-32. [11] 熊青山,彭振斌,殷琨.潛孔錘結構參數優化—遍歷法[J].鑿巖機械氣動工具,2004(2):42-45. [12] 王威,周軍紅,王潤生.多傳感器數據融合的一種方法[J].傳感器技術,2003,22(9):39-41. Approach for performance evaluation of AHP-based INS/gravity matching navigation system* CHEN Jing1, DONG Ming-tao2, CHENG Jian-hua2 (1.Research Institute of Ships,Navy Academy of Armament,Beijing 100073,China;2.Automation College,Harbin Engineering University,Harbin 150001,China) We propose an analytical hierarchy process(AHP)based inertial navigation system(INS)/gravity integrated system accuracy performance evaluation approach.INS/gravity integrated system is firstly analyzed to classify its key error factors.Then we use these factors to establish a multilayer systematic error description model for the application of AHP.To solve the problem of the weight model description of traditional AHP and objectively determine the evaluation weight of each factor,a combined threshold and traverse to determine performance value of system is designed.Finally,a practical application exampleshows the effectiveness of the accuracy performance evaluation approach.This method can evaluate the performance of INS/gravity integration system, and then service for the modification of this system and has certain practical significance. INS/gravity matching navigation; performance evaluation; analytical hierarchy process(AHP); precision; threshold 10.13873/J.1000—9787(2016)09—0023—04 2016—07—27 國家自然科學基金資助項目(61374007,61104036,62173081);中央高校科研業務費專項資金資助項目(HEUCFX41309) U 666.1 A 1000—9787(2016)09—0023—04 陳晶(1966-),女,山東煙臺人,高級工程師,主要從事艦船導航系統的論證與研究工作。4 基于遍歷法確定指標標準值
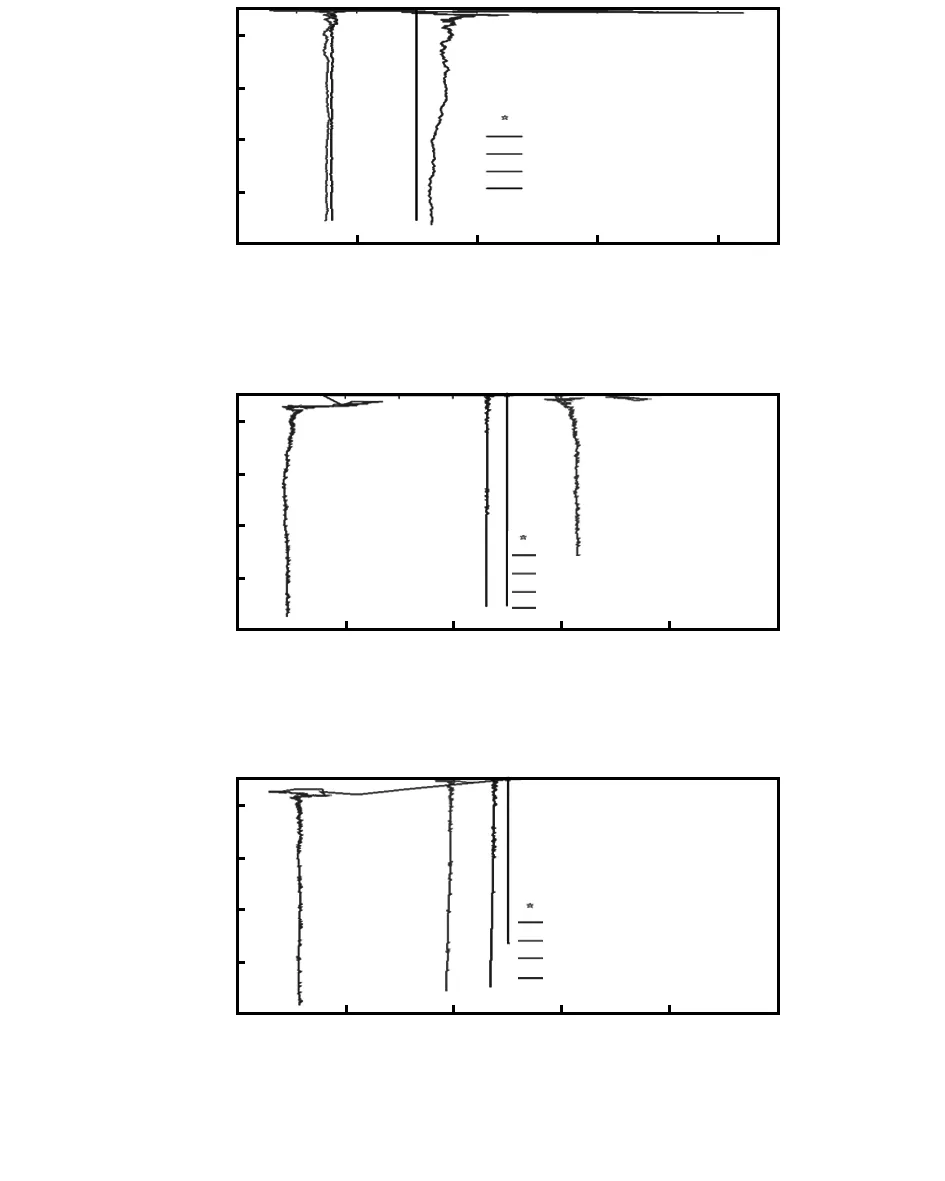
5 仿真實驗與實際算例



6 結 論

