由數轉形，巧解函數難題

● 柯張軍

由數轉形，巧解函數難題

● 柯張軍

一、利用函數圖像，巧解抽象函數不等式

抽象函數不等式是指沒有具體函數解析式的不等式，這類不等式一般利用函數性質求解，畫出符合函數性質的草圖，觀察圖形可以直觀易解。

如在求解這道題：設 f（x）、g（x）分別是定義在R上的奇函數和偶函數，當x＜0時，f（x）g（x）+f（x）g（x）＞0且g（-3）=0，求不等式 f（x）g（x）＜0的解集時，可以先設F（x）=f（x）g（x），因為當x＜0時，f（x）g（x）+ f（x）g（x）=［f（x）g（x）］=F（x）＞0，所以 F（x）在（-∞，0）上是增函數，因為f（x）、g（x）分別是定義在R上的奇函數和偶函數，所以F（x）為 奇 函 數，又 g（-3）=0，所 以F（-3）=f（-3）g（-3）=0，f（x）是奇函數，所以 f（0）=0，故F（0）=0。根據以上特點，不妨構造如圖1所示的符合題意的函數F（x）的圖象，由圖直接觀察出所求解集是（-∞，-3）?（0，3）。

圖1

解題過程中依題意確定函數性質，構造函數F（x），依據性質畫出F（x）草圖，觀察圖像求解，實現抽象問題具體化，復雜問題簡單化。

二、利用函數圖像，比較數的大小

比較大小是高考試題中一個重要題型，利用函數圖形交點位置來確定大小關系，可以避免求值過程中的復雜計算，如果根據題意構造幾個函數，畫出圖像確定交點位置，就可以很快得解。

如在判斷 0.32，log20.3，20.3三個數的大小順序時，可將其看成是三個函數y1=x2，y2=log2x，y3=2x在 x=0.3時，所對應的函數值的大小比較。在同一坐標系內作出這三個函數的圖像（如圖2），從圖像可以直觀地看出當 x=0.3時，所對應的三個點 P1，P2，P3的位置，從而可得出結論：20.3＞0.32＞log20.3。

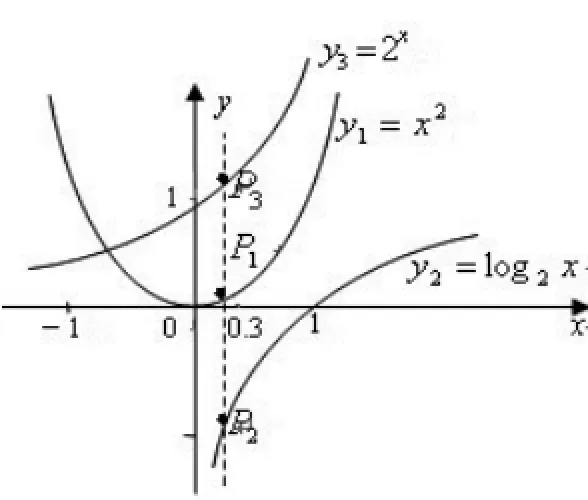
圖2

解題過程中三個數的值不易計算，觀察數式構造函數，使三個數分別為自變量取同一個值的三個不同的函數值，自然想到三個基本初等函數y1=x2，y2=log2x，y3=2x，在同一坐標系中畫出三個函數圖像作圖即可得解。

三、構建解析幾何模型，解決函數最值問題

將函數問題轉化成解析幾何中的斜率、截距、距離等問題，利用其幾何意義求解。與解析幾何有關的常見函數模型有：①距離型函數②斜率型函數；③截距型函數Ax+ By；④單位圓型函數⑤雙曲線型函數

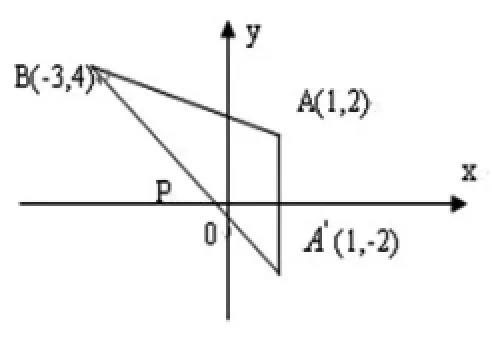
圖3

熟悉幾種與解析幾何有關的常見函數模型，將函數問題轉化為解析幾何問題求解是解決問題的關鍵。

四、利用函數圖像，求參數的取值范圍

方程根的問題，函數零點問題，圖像交點問題，這些問題借助函數圖像，往往可以避免繁瑣計算，獲得簡捷的解答。

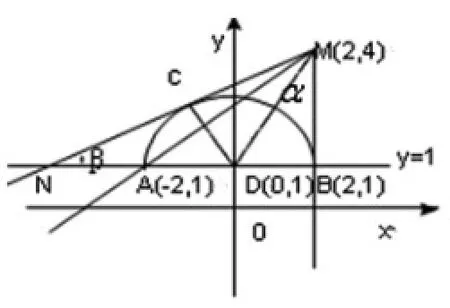
圖4

將方程根的個數問題轉化為直線與圓交點個數問題，利用幾何方法求解直觀簡單。

（作者單位：黃梅縣第一中學）