四邊形添輔助線審題的教學實踐與反思

浙江省紹興市越城區馬山中學　陶苗娟

?

四邊形添輔助線審題的教學實踐與反思

浙江省紹興市越城區馬山中學陶苗娟

添輔助線解幾何題是幾何教學的一部分，也是幾何教學的重難點所在。學生對幾何基本說理過程的掌握存在一定困難。學生達到準確添輔助線解題的程度，顯得難上加難。因而，部分學生對幾何產生畏難情緒。教師在教學中應幫助學生建立信心，使學生仔細審題，充分利用已知條件或圖形隱含信息找到正確的添輔助線方法，使學生形成正確的解題思路。

四邊形 審題 添輔助線 線段相等

解幾何題時，學生有正確的思路是解決問題的關鍵。解題思路與審題息息相關，特別是部分添加輔助線的題目，輔助線添對后題目就豁然開朗，輔助線找不到或者添錯了，不僅解不出題目，還會對解題形成干擾。通過添輔助線，圖形的性質得以顯現，分散的條件得以集中，將新問題轉化為舊問題。幾何證題中，輔助線有橋梁和化難為易的作用。

實際教學中經常碰到的現象是，學生將苦思半天想不出的問題拿來請教教師，教師幫助學生找到關鍵條件稍加點撥或幫助，學生理清思路添加輔助線后恍然大悟。究其原因是學生沒有養成仔細審題的良好習慣，缺少解幾何題的方式方法。

學生對幾何題存在畏難情緒的原因包括：一方面是幾何說理過程寫不清，另一方面是解題時難以形成思路，對已知條件如何有序組合、應用存在困難。特別是普遍條件缺少時，學生不會應用圖形的特征添線、找線，常走彎路而不知及時回頭修改，使解題陷入困境，使幾何成為學生頭痛的學科。教師要幫助學生自我點撥，掌握解幾何題的方法與技巧，找到解題突破口，用正確的方法找到該添的線，掌握一定的審題技巧，形成解題思路。

在《特殊平行四邊形》一章中有通過添輔助線證明兩條線段相等習題。筆者從課本上的一道作業題說起，分析教學中教師如何幫助學生使用問題探究的方式，有效、快速地找到輔助線，使學生在審題過程中碰到問題及時反省，形成正確的解題思路。

已知：如圖，在正方形ABCD中，E、F分別在AD、DC上，且DE=DF，BM⊥EF于M，求證：ME=MF。

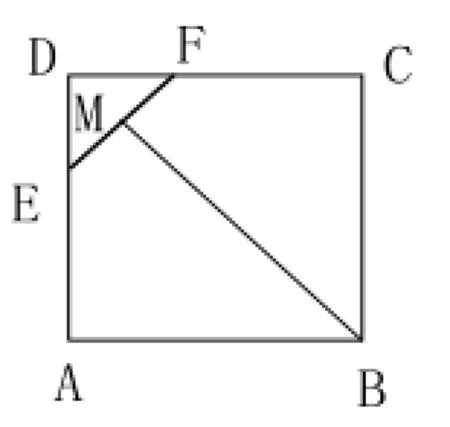
問題分析：練習過程中，筆者發現部分學生添輔助線時連接DM或延長BM，利用等腰三角形“三線合一”的性質說明EM=MF。這樣做忽略了連接DM后，DM與EF是否垂直；忽略了延長BM后，BM的延長線是否經過點D。學生對添加的輔助線沒有進行深入思考，無法繼續解題。筆者設計以下問題啟發學生，幫助學生找到正確的添輔助線的方法。

問題1：證明兩條線段相等有哪些方法？

生答：全等三角形的對應邊相等；等腰三角形兩腰相等，等邊三角形三邊相等，在同一三角形中等角對等邊，三線合一；中垂線上一點到線段兩端的距離相等；角平分線上一點到角兩邊的距離相等；線段中點；平行四邊形的對邊相等，菱形、正方形四邊相等；矩形對角線相等；平行線之間的距離相等；等量代換；三角形中位線等于第三邊一半；直角三角形斜邊上的中線等于斜邊的一半；30°角所對直角邊等于斜邊的一半。

問題2：證明兩條線段相等有很多方法，在具體題目中選擇哪種方法進行證明？同學們在解題時會根據什么選擇方法？

生答：結合已知條件，根據條件的提示選擇方法；根據圖形形狀選擇方法。

問題3：結合以前的解題經驗，同學們能舉例說明嗎？

生答：如果條件中有中點，選中位線，中線或三線合一的方法證明；如果條件中有平行四邊形，應用平行四邊形的性質證明；如果有兩個三角形，證明兩個三角形全等如果出現一個三角形，就證明此三角形為等腰三角形。

問題4：本題中證明EM=MF，結合條件BM⊥EF，你會選擇哪種方法證明？

生答：利用三線合一的性質證EM=MF；利用全等性質證EM=MF。

問題5（針對第一種方法設計）：三線合一的前提條件是等腰三角形，圖中有這樣的等腰三角形嗎？你認為在△DEF中添輔助線能達到目的嗎？如果不行，如何構造等腰三角形？

問題分析：受圖形暗示及思維定式影響，如果出現兩個三角形，學生解題時會用全等證明線段相等。因此，大部分學生證明△ABE≌△ADF。解題過程中，學生容易找到證明全等的兩個條件AB=AD，∠B=∠D，但證明△ABE≌△ADF的第三個條件很難找到。學生用已知條件很難轉化出邊相等或角相等，解題陷入困境。

面對學生的錯誤選擇，筆者在教學中設計以下問題幫助學生正確添加輔助線。

問題1：兩條線段出現在兩個三角形中，證兩條線段相等，我們往往考慮證明這兩個三角形全等，但有時全等的條件不容易找甚至找不到，我們怎么辦？

生答：轉換思路，想其他辦法。

問題2：四邊形問題一般可轉換為三角形問題，結合菱形性質，當菱形中有一個角為60°時，同學們可得到什么結論？

生答：得到等邊三角形。

問題3：四邊形轉化為三角形的問題中，我們常用的添輔助線的方法是什么？同學們想到怎么添輔助線了嗎？

生答：連對角線，連接AC。

教學反思：結合學生產生的思維困惑或理解偏差，筆者從學生需要出發，幫助學生找出問題成因，設計一系列具有針對性的問題，啟迪學生思維，深化問題本質，幫助學生理順解題思路，解決困惑，使學生學會仔細審題，找到正確的輔助線。

筆者通過問題設計引導學生進行發散思維，尋找多種方法解答同一題目并進行方法比較。引導學生對問題進行分類思考，探究條件改變的情況下結論之間的關系。

現代學習方式強調教師通過問題引領學生學習，同時通過學習生成問題，即課堂教學要有“問題”意識。教師在課堂教學中設計問題、提出問題固然重要，但更要關注來自學生的問題，使學生在發現問題、解決問題中成為學習的主人。

教師要鼓勵學生出現學習困惑時問問自己為什么卡住，有哪些地方沒弄明白，碰到一個問題有哪些解決方法等。解題中，學生形成思維障礙的主要原因是學生現有的認知水平不能順應教學內容，造成知識運用上脫節。因此，教師要培養學生樹立問題意識，用問題深化知識發生和發展的關聯，拓展學生思維，提升學生的探究意識，使學生順利理解知識、消除困惑、掌握基本解題技能，使問題成為學生探究性學習的向導。

通過不斷嘗試與探究，學生明白添輔助線是一項難度很大的技巧，出現錯誤并不可怕，關鍵要懂得及時改正。問題探究的過程中，學生學會自己提問、自己解答，這是解決問題的最佳方法。

添輔助線解幾何題時除憑借直覺思維、經驗之外，學生還可應用已知條件的提示或者結論對題目進行邏輯思維與深度思維。學生需要多次嘗試才能成功添加輔助線，尋找輔助線的過程中，學生思維得到訓練、發展和碰撞。學生通過不斷嘗試，仔細審題，自我探究，形成解決問題的方法。

課堂實踐的目的是指導學生掌握審題技巧。教師引導學生少走彎路，及時糾正錯誤。面對錯誤思路，學生要舍得花時間分析錯誤產生的原因，自我交流、思考、總結的過程就是學生思維火花碰撞的過程，是學生自主構建知識網絡的過程。

課堂上，教師應有意識地引導與訓練學生，有利于學生養成良好的審題習慣，有利于學生掌握問題探究、尋找輔助線的方法，使不同學生得到不同發展。

學生需要對題目條件進行深入思考與挖掘，需要鍥而不舍的探究精神及一定量的練習。

［1］倪小芳.巧添輔助線證幾何題［J］.數理化學習（初中版），2013

［2］黨曉燕.找準學生“發展區”創生教學“生長點”——對高三數學教學的幾點體會［J］.寧夏教育科研，2012

ISSN2095-6711/Z01-2016-06-0187