基于穩(wěn)健偏最小二乘法的諧波發(fā)射水平估計

李　湘，陳民鈾，鄭永偉，程　杉

（1.重慶大學電氣工程學院輸配電裝備及系統(tǒng)安全與新技術國家重點實驗室，重慶 400044；2.四川省電力公司內江電業(yè)局，內江 641100；3.三峽大學電氣與新能源學院，宜昌 443002）

?

基于穩(wěn)健偏最小二乘法的諧波發(fā)射水平估計

李湘1，陳民鈾1，鄭永偉2，程杉3

（1.重慶大學電氣工程學院輸配電裝備及系統(tǒng)安全與新技術國家重點實驗室，重慶 400044；2.四川省電力公司內江電業(yè)局，內江 641100；3.三峽大學電氣與新能源學院，宜昌 443002）

摘要：為了合理劃分電力系統(tǒng)及用戶各自的諧波污染責任，文中提出用穩(wěn)健偏最小二乘回歸法估算供電系統(tǒng)諧波阻抗并計算用戶諧波發(fā)射水平。將公共聯接點同步測量采樣獲得的諧波電壓和電流信號作為回歸方程的自變量與因變量，利用穩(wěn)健偏最小二乘求解回歸系數，即系統(tǒng)側諧波阻抗。該方法保留了偏最小二乘法在自變量存在相關性的條件下仍然能夠回歸建模的優(yōu)點，同時有效克服了偏最小二乘法由于對異常值敏感而導致建模結果不準確的缺陷。通過仿真分析和實際工程算例驗證了該方法的準確性和有效性。

關鍵詞：穩(wěn)健偏最小二乘回歸；異常值；回歸系數；系統(tǒng)諧波阻抗；諧波發(fā)射水平

現在，一方面快速發(fā)展的現代社會對電能質量的要求越來越高，而另一方面，大量非線性工業(yè)用戶以及電力電子裝置接入電網，產生了大量諧波，這些諧波的產生將給電力系統(tǒng)設備的安全經濟運行帶來嚴重的危害［1］。為了解決這一矛盾，保證公用電網質量，國際國內都制定了相應的限制標準及抑制措施。國家標準GB/T 14549—93《電能質量公用電網諧波》規(guī)定了用戶諧波發(fā)射限值，而國外提出的獎懲性方案［2］也是通過補償或懲罰系統(tǒng)與用戶的獎懲機制來抑制諧波污染。因此，確定公共聯接點PCC（point of common coupling）處系統(tǒng)及用戶對供電電壓的污染程度，準確估計雙方的諧波發(fā)射水平是目前首先需要解決的問題。

為了準確估計系統(tǒng)及用戶的諧波發(fā)射水平，國內外都做了大量的研究。在定性方面，主要有臨界阻抗法［3］、支持向量機法［4］、功率流向法［5-6］；定量方面，主要包括開關元件法［7］、注入法［8］、參考阻抗法［9］、波動量法［10］以及線性回歸法［11-15］等。從實現方法的復雜性和評估結果的精確性兩方面考慮，現在國內外的主要研究方向為定量分析法。考慮到背景諧波的存在，其主要是利用PCC處的諧波擾動量來估算系統(tǒng)和用戶的諧波阻抗。屬于“干預式”方法的開關元件法和注入法所利用的擾動量是人為方式附加產生的，如向系統(tǒng)注入諧波/間諧波電流、通斷系統(tǒng)某一支路或是啟停負荷本身來估算諧波阻抗。該類方法雖然能夠準確估計系統(tǒng)及負荷參數，但這種“故意”的擾動可能會影響系統(tǒng)的正常運行。而參考阻抗、波動量法及線性回歸法則屬于“非干預式”法，它們利用系統(tǒng)或負荷本身的自然擾動，操作簡單、安全。其中，參考阻抗法在系統(tǒng)與用戶阻抗變化的時候可能會有較大估計誤差，波動量法是根據PCC處諧波電壓、電流量比值來估計諧波阻抗，這就要求測量精度高或測量值有足夠大的波動。線性回歸法通過PCC處的諧波電壓電流值估算系統(tǒng)諧波阻抗，計算簡單實用。從文獻［11-15］逐步深入完善。最新的偏最小二乘法克服了變量相關性對系統(tǒng)建模的不良影響，但未考慮測量值中存在較大誤差或其他異常值時的情況。

針對上述分析，本文提出采用穩(wěn)健偏最小二乘法估計系統(tǒng)諧波阻抗并跟蹤計算用戶諧波發(fā)射水平。穩(wěn)健偏最小二乘算法由于對主成分的提取以及最后的回歸計算均進行了穩(wěn)健化，故能夠克服異常值的影響，獲得更準確的估計結果。電路模型仿真及工程實例均證明了該方法的有效性。

1　諧波發(fā)射水平估算原理

目前，國內外通常以諾頓等效電路作為評估系統(tǒng)與用戶諧波發(fā)射水平的理論模型［13］。為方便構造回歸方程，將其轉化為戴維南-諾頓等效電路［14］，如圖1所示。

圖1　諧波分析的等值電路Fig.1　Basic equivalent circuit for harmonic analysis

圖1中，Zsh、Zch分別為系統(tǒng)側和用戶側的h次等值諧波阻抗；Ush、Ich分別為系統(tǒng)側和用戶側的h次等值諧波源；Uph、Iph則為公共聯接點處的h次諧波電壓及電流，這兩個值可以測量得到。根據圖1電路可得

按照實部和虛部展開得回歸方程為

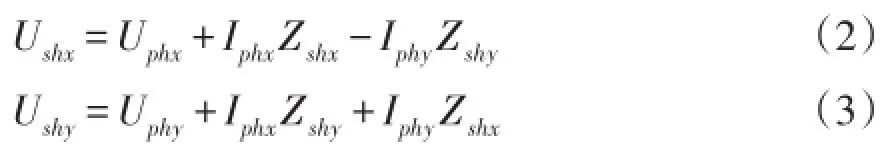
式（2）、式（3）中未知量分別為Ushx、Ushy及Zshx、Zshy，它們?yōu)榛貧w系數，采用穩(wěn)健偏最小二乘法進行回歸求解。Zshx、Zshy即為系統(tǒng)側諧波阻抗。

根據國際電工委員會標準IEC Techical Report 61000-3-6對諧波發(fā)射水平定義：用戶接入系統(tǒng)前后公共聯接點處某次諧波電壓的變化量，諧波發(fā)射水平的計算方程為

而在實際電力系統(tǒng)中，Zsh為系統(tǒng)側短路阻抗，往往遠小于Zch，因而式（4）可簡化為

2　穩(wěn)健偏最小二乘回歸基本原理

假設一個線性回歸模型，其中p個自變量（x1,…,xp）'=Xn×p，q個因變量（y1,…,yp）'=Yn×p，觀測數據為n。有

式中，誤差項ei需滿足E（ei）=0以及COV（ei）=Σe；β0=（β01，…，β0q）'和B'q,p為未知的截距及斜率矩陣。

假設x和y變量通過一個雙線性模型關聯，

從以上兩個模型中可看出，穩(wěn)健偏最小二乘法［15］主要分為兩個階段，第一個階段為構建主成分n,k=（

t?1,…,n，求得因變量y與自變量x與主成分的依賴關系，第二階段則求出因變量y與自變量x的關系。

穩(wěn)健偏最小二乘法的核心在于用穩(wěn)健估計Σxy和Σx取代了Sxy和Sx，以此獲得穩(wěn)健得分向量，同時，用穩(wěn)健回歸取代傳統(tǒng)的多元回歸［17］，這就使得它能夠克服異常值的不良影響而獲得準確的回歸結果。

假定模型中的觀測數據均已標準化，并定義Zn,m=（Xn,p,Yn,q）。為了獲得穩(wěn)健得分向量，首先對Zn,m進行穩(wěn)健主成分分析，這將得到一個穩(wěn)健估計中心向量μz=x,y，而穩(wěn)健得分向量

其中，當第i組觀測值通過穩(wěn)健主成分分析被確定為異常值時，ωi=0，反之，則為1。得到μ與Σ后，則類似偏最小二乘算法為

3　仿真分析

本文為驗證在諧波發(fā)射水平計算中偏最小二乘法對異常值的敏感性以及穩(wěn)健偏最小二乘法對異常值的抗干擾性，根據圖1搭建了仿真模型。

（1）系統(tǒng)側及用戶側的h次諧波源分別為U?sh=50∠51°,I?ch=6.36∠45°。

（2）系統(tǒng)側和用戶側的h次諧波阻抗分別為15+ j30 Ω，25+j300 Ω。

假定系統(tǒng)側諧波阻抗未知，分別利用偏最小二乘法（不含異常值、含異常值情況）和穩(wěn)健偏最小二乘法（含異常值）進行仿真計算，比較3種情況下的仿真值以及仿真值與實際值之間的差異，證明穩(wěn)健偏最小二乘法的抗干擾及其準確性。

在公共聯接點處抽樣h次諧波電壓、電流值500個點，其數據如圖2所示。

將圖2中500個點分為10組，每組50個點。分3種情況對以上數據進行建模分析。第1種為偏最小二乘法回歸建模，所有建模數據均為正常值；第2種仍為偏最小二乘回歸建模，但每組建模數據被加入5個異常值（如圖3所示，舉例其中一組建模數據），它們并不能通過直觀判斷剔除；第3種穩(wěn)健偏最小二乘回歸建模，建模數據同第2種情況相同。這3種情況對系統(tǒng)側諧波阻抗的估計結果見圖4、圖5。其中，左邊的圖中每個坐標上對應的兩個數值分別為式（2）、式（3）中Zshx的估計結果；右邊的圖中每個坐標上對應的兩個數值則分別為式（2）、式（3）中Zshy的估計結果。

3種情況下，每組系統(tǒng)側諧波阻抗的估計值與實際值的誤差見表1。每組阻抗估計值均為式（2）、（3）中所求結果的平均值。

圖2　h次諧波電壓、電流幅值波形Fig.2　Magnitude waveforms of the hth harmoinc voltage and current at PCC

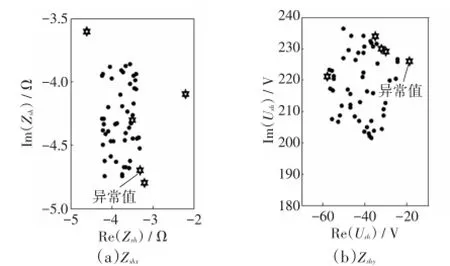
圖3　50個樣本點及5個異常值Fig.3　50 sample points of voltage and current at PCC and five outliers

圖4　情況1與情況2的h次系統(tǒng)諧波阻抗估計值Fig.4　The hth harmonic impedance of power system in case 1 and case 2

圖5　情況1與情況3的h次系統(tǒng)諧波阻抗估計值Fig.5　The hth harmonic impedance of power system in case 1 and case 3

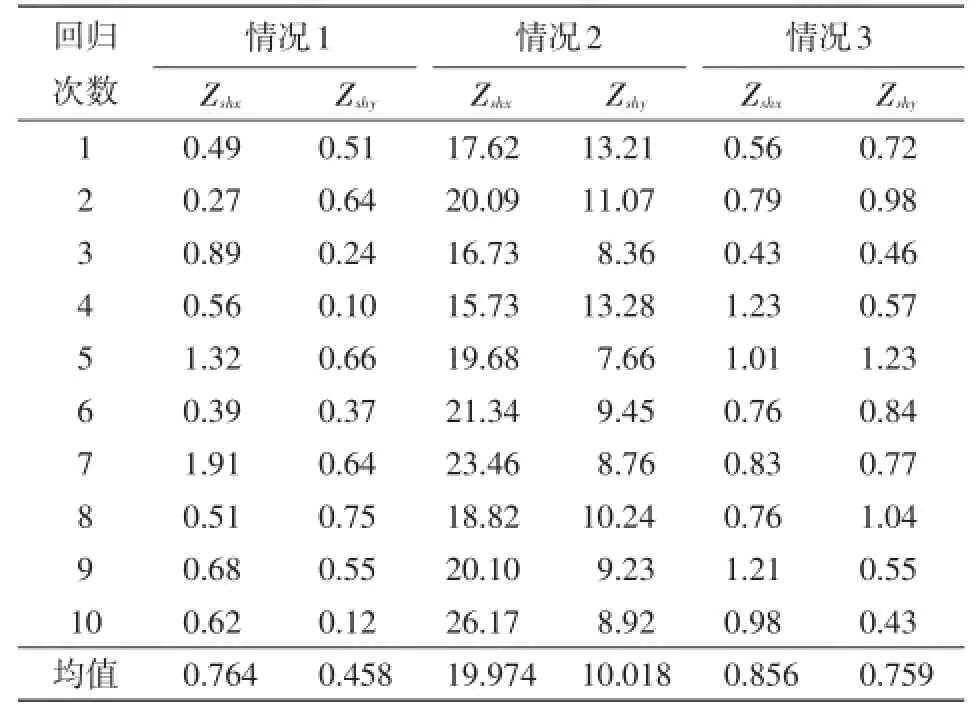
表1　3種情況下系統(tǒng)阻抗估計值的誤差Tab.1　Comparison of errors of Zshin three cases %

通過表1可以看出，雖然偏最小二乘法的估計結果精度較高，但當建模數據中含有一部分異常值時，其估計誤差將大幅升高，且從圖4和圖5中可看出式（2）、（3）的估計結果相差較大；而采用穩(wěn)健偏最小二乘回歸則幾乎完全避免了異常值的不良影響，仍然能夠獲得精度較高的估計結果，式（2）、（3）的估計結果也基本一致，這樣也將使得諧波發(fā)射水平的估計更為準確。

根據式（5），采用穩(wěn)健偏最小二乘法的估計結果，定量計算用戶諧波發(fā)射水平為

Uch≈||Zsh||Iph=33.557×5.752 5=193.037V（18）約占PCC點諧波電壓的86.91%。

4　實例分析

在這一部分中，將采用穩(wěn)健偏最小二乘法估計實際系統(tǒng)的5次諧波阻抗，并以此計算用戶側某鋼廠的諧波發(fā)射水平。實測數據為重慶青杠變電站35 kV母線上電壓、電流。根據相關資料，系統(tǒng)在最小運行與最大運行方式下，35 kV母線的短路容量分別為120.8 MVA和250 MVA。

錄波儀采樣頻率為6 400 Hz，采樣20 s，把原始采用數據分為500段，分別進行FFT變換，獲得的5次諧波電壓、電流波形如圖6所示。

圖6　5次諧波電壓、電流波形Fig.6　Magnitude waveforms of 5th harmonic voltage and current at PCC

將以上500個數據分成20組，每組25個數據，利用穩(wěn)健偏最小二乘回歸法估算系統(tǒng)側系統(tǒng)阻抗，結果如圖7所示。

圖7　5次系統(tǒng)諧波阻抗值Fig.7　The 5th harmonic impedance of power system

根據母線最大與最小短路容量，可算出相應的參考基波阻抗分別為5.476 Ω與11.333 Ω。而系統(tǒng)側5次諧波電抗的估計值為48.12 Ω，計算出基波阻抗估計值為9.624 Ω，在參考基波阻抗變化范圍內。此結果證明了穩(wěn)健偏最小二乘法的準確性。

系統(tǒng)側5次諧波阻抗的平均值為48.276 Ω，根據式（5），PCC處諧波電壓的均值為332.217 6 V，用戶諧波發(fā)射水平為82.827 V，約占PCC點處5次諧波電壓的24.93%。由于此鋼廠容量較小，故其諧波發(fā)射較低，對公用電網的電能質量影響較低。

5　結語

本文針對偏最小二乘回歸法對異常值敏感的缺陷，提出了將穩(wěn)健偏最小二乘回歸法應用于諧波發(fā)射水平的估算中。該方法在建模數據中含有部分異常值時仍然能夠獲得準確的估計結果，具有較強的穩(wěn)健性。以此估計結果計算諧波發(fā)射水平將更準確劃分系統(tǒng)及用戶的污染責任。仿真計算及實際分析均證明了此方法的精確性和有效性，具有較強的工程應用前景。

參考文獻：

［1］彭祥華，周群，曹曉燕（Peng Xianghua，Zhou Qun，Cao Xiaoyan）.一種高精度的電網諧波/間諧波檢測的組合優(yōu)化算法（A high precision combinational optimization algorithm of power grid harmonic/inter-harmonic signal detection）［J］.電力系統(tǒng)保護與控制（Power System Pro?tection and Control），2014，42（23）：95-100.

［2］Toma? P，Bo?tjan B，Igor P.Harmonic contributions evalu?ation with the harmonic current vector method［J］.IEEE Transactions on Power Delivery，2008，23（1）：425-433.

［3］于淼，張炳達（Yu Miao，Zhang Bingda）.配電網中諧波源檢測方法的研究（Study of detecting harmonic sources method in distribution systems）［J］.電力系統(tǒng)及其自動化學報（Proceedings of the CSU-EPSA），2005，17（1）：36-40，87.

［4］馬歷，劉開培，雷肖（Ma Li，Liu Kaipei，Lei Xiao）.配電網諧波源定位的支持向量機估算法（Support vector ma?chine estimating algorithm of harmonic source localization in power distribution network）［J］.中國電機工程學報（Proceedings of the CSEE），2008，28（10）：111-116.

［5］Xu W.Power direction method can not be used for harmon?ic source detection［C］//IEEE Power Engineering Society Summer Meeting Seattle，USA：2000.

［6］Li C，Xu W，Tayjasanant T.A“critical impedance”-based method for identifying harmonic sources［J］.IEEE Transac?tions on Power Delivery，2004，19（2）：671-678.

［7］Palethorpe B，Sumner M，Thomas D W P.Power system impedance measurement using a power electronic convert?er［C］//Proceedings of 9th International Conference on Harmonics and Quality of Power.USA，2000.

［8］Tsukamoto M，Kouda I，Natsuda Y，et al.Advanced meth?od to identify harmonics characteristic between utility grid and harmonic current sources［C］//Proceedings of 8th International Conference on Harmonics and Quality of Power.Greece，1998.

［9］ Xu W，Liu Y L.A method for determining customer and utility harmonic contribution at the point of common cou?pling［J］.IEEE Transactions on Power Delivery，2000，15 （2）：3-16.

［10］Huang X Q，Nie P，Gong H L.A new assessment method of customer harmonic emission level［C］//Power and Ener?gy Engineering Conference.Asia-Pacific，2010.

［11］Chataigner J C.Methods for separating customer and sup?ply-side harmonic contributions［R］.Paris：EDF&CNAM，1996.

［12］張巍，楊洪耕（Zhang Wei，Yang Honggeng）.基于二元回歸的諧波發(fā)射水平評估方法（A method for assessing harmonic emission level based of binary linear regression）［J］.中國電機工程學報（Proceedings of the CSEE），2004，24（6）：50-54.

［13］車權，楊洪耕（Che Quan，Yang Honggeng）.基于穩(wěn)健回歸的諧波發(fā)射水平評估方法（Assessing harmonic emis?sion level based on robust regression method）［J］.中國電機工程學報（Proceedings of the CSEE），2004，24（4）：39-44.

［14］黃舜，徐永海（Huang Shun，Xu Yonghai）.基于偏最小二乘回歸的系統(tǒng)諧波阻抗與諧波發(fā)射水平的評估方法（Assessing harmonic impedance and the harmonic emis?sion level based on partial least squares regression meth?od）［J］.中國電機工程學報（Proceedings of the CSEE），2007，27（1）：93-97.

［15］李麗，馬宏忠，姜寧，等（Li Li，Ma Hongzhong，Jiang Ning，et，al）.基于改進偏最小二乘法的系統(tǒng)諧波阻抗及諧波發(fā)射水平估算（Assessing harmonic impedance and the harmonic emission level based on improved par?tial least-squares regression method）［J］.電力系統(tǒng)保護與控制（Power System Protection and Control），2011，39 （1）：92-95，131.

［16］Hubert M，Branden K V.Robust methods for partial least squares regression［J］.Journal of Chemometrics，2003，17 （10）：537-549.

［17］Hastie T，Tibshirani R J，Friedman J.The elements of sta?tistical learning［M］.New York：Springer，2009.

李湘（1988—），女，碩士研究生，研究方向為諧波分析及諧波治理，E-mail：liandheqc@163.com

陳民鈾（1954—），男，教授，博士，博士生導師，研究方向為計算智能及其在電力系統(tǒng)中的應用、分布式發(fā)電技術、智能電網，E-mail：mchencqu@126.com

鄭永偉（1985—），男，碩士研究生，研究方向為分布式發(fā)電技術、微網運行控制，E-mail：aoyun200888pm8@126.com

中圖分類號：TM744

文獻標志碼：A

文章編號：1003-8930（2016）06-0086-05

DOI：10.3969/j.issn.1003-8930.2016.06.015

作者簡介：

收稿日期：2014-04-04；修回日期：2015-03-24

Assessing Harmonic Emission Level Based on Robust Partial Least Squares Regression

LI Xiang1，CHEN Minyou1，ZHENG Yongwei2，CHENG Shan3
（1.State Key Laboratory of Power Transmission Equipment&System Security and New Technology，Institute of Electrical Engineering,Chongqing University，Chongqing 400044，China；2.Neijiang ElectricPower Bureau of Sichuan Electric Power Corporation,Neijiang 641100，China；3.College of Electric Engineering and New Energy，China Three Gorges University，Yichang 443002，China）

Abstract：In order to divide the harmonic pollution liability of power system and users rationally，a novel method to eval?uate harmonic contributions at the point of common coupling（PCC）is presented in this paper.The proposed approach is based on robust partial least squares regression（robust PLS）.As regression coefficients-system harmonic impedance are estimated based on robust PLS by utilizing the signals of harmonic voltage and current measured synchronously at PCC.Consequently the harmonic emission level of user is calculated.The presented method overcomes the disadvantage of variable dependence in establishing of the system model and reduces or removes the effect of outlying data points. The method was proved to be valid and feasible by the simulation analysis and extensive engineering example.

Key words：robust partial least squares regression；outliers；regression coefficient；system harmonic impedance；har?monic emission level