計及運行風險的電力系統優化調度方法

李　燦，曾　沅，秦　超，宋云亭，吉　平，吳　威

（1.天津大學智能電網教育部重點實驗室，天津 300072；2.中國電力科學研究院，北京 100192；3.國網福建省電力有限公司經濟技術研究院，福州 350012）

?

計及運行風險的電力系統優化調度方法

李燦1，曾沅1，秦超1，宋云亭2，吉平2，吳威3

（1.天津大學智能電網教育部重點實驗室，天津 300072；2.中國電力科學研究院，北京 100192；3.國網福建省電力有限公司經濟技術研究院，福州 350012）

摘 要：針對現有優化調度方法在考慮風險因素時過于單一、片面的現狀，該文考慮風電波動、機組停運、線路故障、負荷波動等多種不確定因素的影響，以電壓越限和潮流越限衡量系統整體的運行風險，構建了能夠計及系統面臨風險的多目標優化調度模型。該模型以運行風險和發電成本為目標函數，將隨機潮流理論引入到發電優化調度中，并針對不同的天氣狀況，對線路故障概率進行實時修正以期更加接近實際運行環境。結合多目標粒子群算法及模糊集理論對所建立的模型進行求解，算例結果表明所提模型和方法能夠處理不確定因素對系統運行風險的影響，并反映不同天氣狀況下調度方案的差異性，為實施短期優化調度提供有益參考。

關鍵詞：優化調度；運行風險；不確定因素；隨機潮流

隨著我國區域電網的互聯，風電并網容量的逐年增加以及電力市場的逐步建設，電力系統優化調度問題面臨的復雜性日益增加。傳統的電力系統優化調度問題通常是在考慮系統功率平衡、機組出力不越限等一系列約束條件的前提下，以系統總發電費用最小為目標，對發電廠各機組出力進行優化分配［1-2］。但往往過于關注經濟性而忽略了調度運行中的其他因素，無法適應電力系統的發展需要。

文獻［3-5］以節能、經濟、環保三大原則為目標，建立了多目標優化調度模型。但這些方法均未對系統的安全可靠性給予太多的重視。目前有關電網風險的研究主要圍繞靜態安全評估［6-7］、輸電斷面輸電能力分析［8］、暫態安全評估［9-10］等方面，取得了大量成果。而近年來在優化調度領域引入風險理論已成為研究人員的研究熱點。文獻［11］引入棄風懲罰因子，建立了考慮系統安全風險的優化調度模型，但該模型只關注了風機出力對系統風險的影響，而忽略了影響系統風險的其他因素。文獻［12］考慮發電資源消耗最少、能源環境效益最好、系統安全穩定程度最高等因素，提出了含風電場的多目

5）系統旋轉備用約束標優化調度模型，但該模型僅以電壓穩定指標衡量系統的安全性。文獻［13］定義了運行風險，針對線路故障，構建了基于風險的多目標經濟調度模型，但未考慮風電出力的波動性對于系統運行風險的影響。文獻［14-15］建立了計及風險的風電并網系統的優化調度模型，但涉及的風險均為考慮風電并網影響的系統備用風險，并未考慮系統整體的運行風險。文獻［16-17］計及冰凍災害對輸電線路的影響，建立了考慮天氣因素的機組優化方法。綜上，現有的優化調度方法在考慮風險因素時大多只考慮了個別不確定因素的影響。

本文考慮風電波動、機組停運、線路故障、負荷波動等多種不確定因素的影響，以電壓越限和潮流越限衡量系統的運行風險，構建了計及運行風險的多目標優化調度模型。該模型以系統運行風險和發電成本為目標函數，通過將隨機潮流理論引入優化調度問題，以其宏觀統計特性處理系統中不確定因素對運行風險的影響，并在計算中針對不同天氣狀況對線路故障概率進行修正，從而更加接近實際運行環境。為求解該模型，采用多目標粒子群算法與模糊集理論來確定最優方案，最后以IEEE-14節點測試系統為例來證明本文所述方法的有效性。

1　計及運行風險的優化調度模型

電力系統優化調度分為單時段靜態優化調度和多時段動態優化調度。多時段動態優化調度是在單時段靜態優化調度的基礎上考慮了不同時間斷面的耦合性。為簡化計算，驗證本文所提方法的可行性，文中僅針對單時段建立了優化調度模型。

1.1目標函數

電力系統中節點電壓和支路潮流是否處于合理的區間內，對電力系統的運行安全性至關重要，因此節點電壓和支路潮流的越限風險可以很好地衡量系統整體的運行風險。本文以系統的運行風險和各火電廠的發電成本為目標函數，構建了計及運行風險的多目標優化調度模型，其數學表達式為

式中：Ng為系統中常規發電機組的數量；pi為機組i的有功出力；fi（pi）為機組i的耗量特性，一般用二次函數近似表示，即 fi（pi）=aip2i+bipi+ci，其中ai、bi、ci為機組i的耗量特性參數；Nl為系統中支路的數量；Rli為第i條支路的越限風險；Nn為系統中PQ節點的數量；Rui為第i個PQ節點的電壓越限風險。

1.2約束條件

1）系統功率平衡約束

式中：Pi、Qi分別為節點i的發電機有功出力和無功出力；Pw、Qw分別為風機的有功出力和無功出力；Pdi、Qdi分別為節點i的有功負荷和無功負荷；φij為節點i和 j的電壓相角差；Gij、Bij分別為支路i、j的電導和電納。

2）常規發電機出力約束

式中，Pim

ax、Pimin和Qmiax、Qmiin分別為發電機i有功和無功出力的上下限。

3）節點電壓約束

式中，Uim

ax、Uimin分別為節點i的電壓上下限。

4）線路傳輸功率約束

式中，Smaxli為線路i的傳輸極限。

式中：Sui、Sd

i分別為常規機組i提供的正、負旋轉備用容量；PL為系統的總負荷；L%分別為系統總負荷預測誤差對正旋轉備用的需求；Pwmax為風機的最大出力；Pw為風機的有功出力；wu%、wd%分別為風機出力預測誤差對正、負旋轉備用的需求。

2　基于隨機潮流的運行風險

隨機潮流可以考慮多種不確定因素的影響，以其數學模型為基礎，通過概率理論得到系統運行狀況的宏觀統計信息。相比于傳統的確定性潮流分析，能夠以較小的計算量更加全面、深刻地展現系統的運行特性。因此本節采用隨機潮流處理風電波動、負荷波動、機組停運、線路故障等不確定因素，并以此為基礎計算優化調度模型中的運行風險F2。

2.1不確定因素的數學模型

1）風電出力的不確定性

風機的種類多種多樣，其中雙饋風電機組是目前主流的風電機組，其有功出力和風速的關系為

式中：Pr為風電機組額定有功出力；vci為切入風速；vr為額定風速；vco為切出風速；k1、k2為風速介于切入風速和額定風速之間時風機有功出力函數的相關系數，具體表達式為

根據實際的統計，一般情況下風速都是維持在切入風速和額定風速的范圍內，根據在此區間內風機有功出力與風速之間的近似線性關系，并結合風速的威布爾分布模型，可以得到風機有功出力的概率密度函數為

式中，k、c分別為威布爾分布的形狀參數和尺度參數。

雙饋風機一般以恒功率因數方式運行，因此其無功出力的概率密度函數可表示為

式中，α為功率因數角。

2）負荷的波動性

大量相關文獻以及長期的實踐表明，負荷的隨機波動服從正態分布。其概率密度函數可表示為

式中：μP、σP為有功功率的期望值和標準差；μQ、σQ為無功功率的期望值和標準差。

3）常規發電機的強迫停運

常規發電機模型只有正常運行和故障停運兩種狀態，因此其隨機特性可以用二項分布來描述：

式中：p為發電機組的可用概率；SN為發電機組的額定容量。

4）線路故障

在中長期風險評估中通常是根據多年的統計數據得到線路的故障概率，并未考慮到不同時間不同區域線路故障概率的差別；在實時運行風險評估中為更加接近系統的實際運行環境，有必要對線路的故障概率進行實時修正。

針對不同的天氣狀況，對線路故障概率按如下方法進行修正［18］，即

式中：p（line）為修正后的線路故障概率；p0（line）為歷史統計線路故障概率；w為天氣影響因子。

天氣影響因子的取值根據天氣的不同而有所不同，具體如表1所示。

表1　不同天氣下的天氣影響因子Tab.1　Weather factors under different weather

通過修正后的線路故障概率，可以得到第i種線路故障情況發生的概率p（li）為

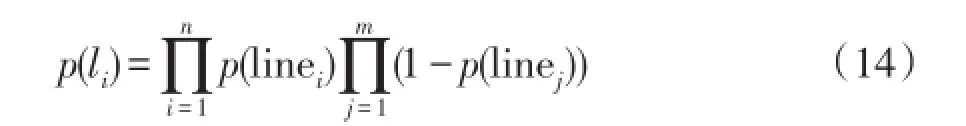
式中，m、n分別為非故障線路和故障線路。

對于由指定的故障線路組成的預想事故集，各種線路故障情況發生的概率之和必然為1，因此第i種線路故障情況發生的概率可以定義為

2.2隨機潮流

電力系統的節點功率和支路潮流可概括為

式中：W為節點注入功率；Z為支路潮流；X為節點電壓；f為功率方程；g為支路潮流方程。

利用泰勒級數將式（16）在系統基準運行點處展開，忽略二次及以上高次項可得

式中：ΔW、ΔX、ΔZ表示注入功率的隨機擾動量以及對應的節點電壓和支路潮流的隨機變化量；J0表示潮流計算最后一次迭代所用的雅可比矩陣；，X0表示基準運行點處電壓的期望值。

式（17）即為隨機潮流的數學模型，而為了處理線路故障，本文借鑒文獻［19］的全概率理論。

全概率理論的表達式為

將其應用到電力系統隨機潮流中，表達式各變量被賦予電力系統新的含義：P（A）為考慮線路故障的系統隨機潮流；Bi為第i種線路故障情況；P（Bi）為第i種線路故障情況發生的概率p′（li）；P（A|Bi）為第i種線路故障情況下的系統隨機潮流。

本文為減少計算量，采用半不變量法與Gram-Charlier級數相結合，對隨機潮流模型進行求解，近似擬合出系統各節點電壓、支路潮流的概率密度函數和累積分布函數。

2.3系統運行風險

在實際電網運行中，當某一節點的電壓或者某一支路的潮流發生越限時，可能會造成相應的保護裝置動作，導致在保護裝置動作期間系統出現一定程度的負荷損失。在電力市場環境下，可以采用貨幣的形式來衡量系統的負荷損失，因此，當系統出現越限情況時，其后果的嚴重程度可表示［20］為

式中：當越限情況i為節點i電壓越限時，Li為節點i處的切負荷量，當越限情況i為支路i潮流越限時，Li為支路i越限導致的切負荷量；Ti、Ci分別為越限情況i導致的停電事故的恢復時間和單位平均成本；Di為因供電合同中斷而帶來的懲罰成本。

節點電壓和支路潮流越限的概率［20-21］分別為

式中：Uim

ax、Uimin分別為節點i的電壓上下限；F（x）為累積分布函數；1-F（Uimax）為節點i電壓超過上限的概率；F（Uimin）為節點i電壓低于下限的概率；

pmlia

x為線路i輸送有功功率的上限；1-F（pmliax）為線路i潮流超過上限的概率。

根據上述節點電壓和支路潮流的越限概率及相應的后果嚴重度，可以得到節點電壓越限和支路潮流越限的風險分別為

通過式（22）即可求得所有PQ節點的電壓越限風險和所有支路的潮流越限風險，從而得到系統整體的運行風險F2。

3　優化調度模型的求解

許多文獻在求解多目標優化問題時大多沒有考慮各優化目標之間的沖突性，只是簡單地采用加權的方法轉化為單目標問題進行求解。因此并不能準確地求解多目標優化調度問題。多目標粒子群算法（MPSO）是一種基于群體智能的演化算法，針對多個目標函數，采用Pareto支配的概念構造非支配解集，即

若決策向量P1、P2都屬于可行解，那么當且僅當式（23）成立時，稱P1支配P2。

將當前找到的非支配解按以下規則保存在外部檔案中：當外部檔案個體數小于設定值時，非支配解直接加入外部檔案；當外部檔案個體數達到設定值時，如果新解支配了外部檔案的部分個體，則新解取代受支配的那些個體，否則根據自適應網格法［22］移除一個個體，將新解加入檔案中。隨著迭代過程不斷維護外部檔案，最后，根據一定的策略從外部檔案中選取一個折中解作為優化問題的最優解，將其應用到本文的電力系統優化調度模型中，具體流程如圖1所示。最終得到的外部檔案即為優化調度方案的Pareto最優解集。

本文采用模糊決策方法從Pareto最優解集中選取一個最優折中解作為最終調度方案［23］。具體做法如下：

對每個目標函數進行模糊化處理，其隸屬度函數為

式中，fimax、fimin分別為第i個目標函數的最大值和最小值，其中i∈No，No為目標函數的個數。

每個Pareto最優解的每個目標函數的隸屬度對應于調度運行人員對該目標函數的滿意度。而調度運行人員對于每個Pareto最優解的滿意度可表示為

通過計算Pareto最優解集中每個解的M值，并進行大小排序，選出M值最大的Pareto最優解作為該優化調度問題的最優折中解。

圖1　多目標粒子群算法流程Fig.1　Flow chart of MPSO

4　算例分析

采用IEEE-14節點系統，對本文所提出的方法進行驗證。該系統的接線圖和具體參數見文獻［23］，所有功率數據都是以100 MVA為功率基值的標幺值。對于發電機節點，除2號節點的發電機的強迫停運率為0.09，其余的發電機節點的發電機的強迫停運率均為0.08。負荷均以IEEE-14節點系統的負荷值為均值，取其10%為標準差，且各負荷相互獨立。假定負荷預測最大誤差和風電功率最大誤差對旋轉備用的需求分別為10%和30%，各節點電壓的閾值設為［0.95，1.05］，各支路潮流的傳輸極限為優化前其傳輸功率的1.2倍。對于節點電壓越限，假定切除該節點30%的負荷后，系統恢復正常運行［21］；對于支路潮流越限，則假定就近切除線路兩端30%的負荷后，系統恢復正常運行［20］。

為計及風電場對于系統的影響，在系統的14號節點處通過變壓器和110 kV輸電線路引入風電場。風電場采用雙饋異步風機，切入風速是3 m/s，切出風速是25 m/s，額定風速是14 m/s，其接入部分的參數見表2。

表2　風電場的相關參數Tab.2　Related parameters of wind farm

對于線路故障，假設該系統中只有線路2～4和線路7～9易發生故障，且前者易遭遇雷雨天氣，后者易遭遇大霧天氣，表3給出了兩條線路在正常天氣下以及在惡劣天氣下經天氣影響因子修正后的線路故障概率。

表3　不同天氣下線路故障概率Tab.3　Line fault probabilities under different weather conditions

在優化前，分別針對未接入風電、接入風電、接入風電并考慮線路故障3種情況對系統進行隨機潮流分析，以節點4的電壓為例，其概率密度函數（PDF）和累積分布函數（CDF）如圖2和圖3所示。可以看出，風電的接入以及線路故障增大了電壓的期望值及波動范圍，從而增大了系統的越限風險。

圖2　節點4電壓概率密度函數Fig.2　Voltage PDF of node 4

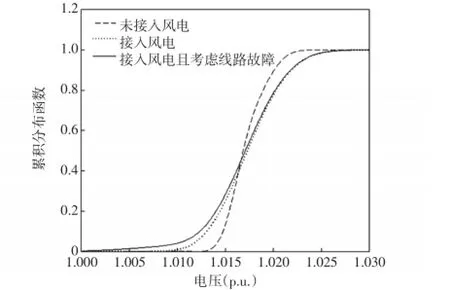
圖3　節點4電壓累積分布函數Fig.3　Voltage CDF of node 4

以系統接入風電未考慮線路故障的情況為例，采用多目標粒子群算法對系統進行優化，得到的Pareto最優解集如圖4所示。從Pareto最優解的分布來看，前沿分布相對均勻，具有良好的多樣性，證明了本文所設計程序的有效性。

圖4　未考慮線路故障的Pareto最優解集Fig.4　Pareto optimal solution set without considering line fault

系統接入風電后，針對不同的場景，得到優化后各運行風險和發電成本的結果如表4所示，對應的各個發電機出力情況如表5所示。其中，優化前不考慮線路故障，場景1為不考慮線路故障，場景2為考慮正常天氣下線路故障，場景3為考慮惡劣天氣下線路故障。

表4　不同場景下系統的運行風險和發電成本Tab.4　Operation risk and generation cost of the system under different scenarios

表5　不同場景下各發電機出力情況Tab.5　Output of the generators under different scenarios

從上述優化結果中可以看出，優化之前雖然系統的發電成本較低，但系統的運行風險卻很高，在不考慮線路故障的情況下，對系統進行發電優化，雖然發電成本有所增加，但系統的運行風險卻大大降低，優化方案取得了很好的效果。而在考慮線路故障的情況下，相比不考慮線路故障，運行風險的增幅明顯高于發電成本的增幅，主要是因為當這些線路發生故障時，系統結構發生改變，導致潮流轉移，與這些線路相鄰的線路和節點發生潮流越限和電壓越限的概率隨之增加，從而增大了系統的運行風險。而對比不同天氣狀況下的優化情況，可以看出系統在惡劣天氣下的風險要高于正常天氣下的，與實際相符，并且系統各個機組的出力狀況也有所不同，體現了不同天氣狀況下調度方案的差異性。

5　結語

電力系統的運行環境日益嚴峻，忽略系統風險的電力系統優化調度愈發顯得保守。而現有研究成果往往只注重個別風險因素對于系統運行風險的影響，不能很好地反映系統整體的運行風險。本文提出了一種計及運行風險的優化調度模型，以系統運行風險和發電成本作為目標函數。該模型將隨機潮流理論引入優化調度，以其宏觀統計特性來處理風電出力、負荷波動、發電機強迫停運、線路故障等一系列不確定因素的影響，并針對不同的天氣狀況，對線路的故障概率進行實時修正從而更加接近實際運行環境。求解模型時為體現不同目標間的競爭關系，采用多目標粒子群算法及模糊決策理論進行求解。實例證明所提模型及方法可很好地處理各種不確定因素的影響，并體現不同天氣狀況下調度方案的差異性，適合于實際的短期優化調度。

本文僅針對單個時段建立了優化調度模型，且在評估系統越限后果時，采用按一定百分比切除越限節點負荷和過載支路兩端節點負荷的方法。如何考慮不同時間斷面的耦合性，將其應用到動態優化調度之中，并且更加準確地評估系統越限后果，將是本文下一步研究工作的重點。

參考文獻：

［1］胡澤春，丁華杰，孔濤（Hu Zechun，Ding Huajie，Kong Tao）.風電-抽水蓄能聯合日運行優化調度模型（A joint daily operational optimization model for wind power and pumped-storage plant）［J］.電力系統自動化（Automation ofElectricPowerSystems），2012，36（2）：36-41，57.

［2］Vlachogiannis J G，Lee K Y.Quantum-inspired evolution?ary algorithm for real and reactive power dispatch［J］. IEEE Trans on Power Systems，2008，23（4）：1627-1636.

［3］李學斌（Li Xuebin）.機組負荷分配的多目標優化和多屬性決策（Multi-objective optimization and multi-attri?bute decision making analysis for economic load dispatch）［J］.電力系統及其自動化學報（Proceedings of the CSUEPSA），2010，22（1）：142-145.

［4］Niknam T，Azizipanah-Abarghooee R，Zare M，et al.Re?serve constrained dynamic environmental/economic dis?patch：a new multiobjective self-adaptive learning bat al?gorithm［J］.IEEE Systems Journal，2013，7（4）：763-776.

［5］陳碧云，韋杏秋，陳紹南，等（Chen Biyun，Wei Xingqiu，Chen Shaonan，et al）.基于多種群遺傳算法的電力系統多目標優化（Power system multi-objective optimization based on multi-population genetic algorithm）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（7）：24-29.

［6］張理（Zhang Li）.含風電場的發輸電系統運行風險評估（Operation Risk Assessment of Generation and Transmis?sion System Containing Wind Farms）［D］.杭州：浙江大學電氣工程學院（Hangzhou：College of Electrical Engi?neering，Zhejiang University），2013.

［7］路攀，李雪，王春亮（Lu Pan，Li Xue，Wang Chunliang）.負荷相關的風電并網系統線路過載風險控制（Risk control of transmission line overload for wind power inter?connected grid with correlated load）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27 （11）：16-20.

［8］崔曉丹，方勇杰，周霞，等（Cui Xiaodan，Fang Yongjie，Zhou Xia，et al）.基于風險的輸電斷面經濟輸電功率計算（Risk-based economical transmission power calcula?tion of transmission sections）［J］.電力系統自動化（Auto?mation of Electric Power Systems），2014，38（8）：30-34.

［9］劉新東，江全元，曹一家，等（Liu Xindong，Jiang Quanyu?an，Cao Yijia，et al）.基于風險理論和模糊推理的電力系統暫態安全風險評估（Transient security risk assess?ment of power system based on risk theory and fuzzy rea?soning）［J］.電力自動化設備（Electric Power Automation Equipment），2009，29（2）：15-20.

［10］宋曉喆，汪震，甘德強，等（Song Xiaozhe，Wang Zhen，Gan Deqiang，et al）.臺風天氣條件下的電網暫態穩定風險評估（Transient stability risk assessment of power grid under typhoon weather）［J］.電力系統保護與控制（Power System Protection and Control），2012，40（24）：1-8.

［11］徐帆，王穎，楊建平，等（Xu Fan，Wang Ying，Yang Jian?ping，et al）.考慮電網安全的風電火電協調優化調度模型及其求解（Generation scheduling model and applica?tion for wind-thermal power system considering security constraints）［J］.電力系統自動化（Automation of Electric Power Systems），2014，38（21）：114-120.

［12］陳道君，龔慶武，張茂林，等（Chen Daojun，Gong Qing?wu，Zhang Maolin，et al）.考慮能源環境效益的含風電場多目標優化調度（Multi-objective optimal dispatch in wind power integrated system incorporating energy-envi?ronmental efficiency）［J］.中國電機工程學報（Proceed?ings of the CSEE），2011，31（13）：10-17.

［13］邱威，張建華，劉念，等（Qiu Wei，Zhang Jianhua，Liu Nian，et al）.計及運行風險的多目標發電優化調度（Multi-objective optimal generation dispatch with consid?eration of operation risk）［J］.中國電機工程學報（Pro?ceedings of the CSEE），2012，32（22）：64-72.

［14］欒士巖（Luan Shiyan）.計及風力發電風險的電力系統優化調度研究（Research on Optimal Scheduling of Pow?er System Considering Wind Power Risk）［D］.上海：上海交通大學電子信息與電氣工程學院（Shanghai：School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University），2010.

［15］姚瑤，于繼來（Yao Yao，Yu Jilai）.計及風電備用風險的電力系統多目標混合優化調度（Multi-objective hybrid optimal dispatch of power systems considering reserve risk due to wind power）［J］.電力系統自動化（Automation of Electric Power Systems），2011，35（22）：118-124.

［16］陳皓勇，胡斌，葉榮（Chen Haoyong，Hu Bin，Ye Rong）.計及氣象災害因素的電網規劃方法（Transmission net?work planning considering weather disaster）［J］.電網技術（Power System Technology），2009，33（20）：82-87.

［17］張永熙（Zhang Yongxi）.極端氣象災害下考慮不確定斷線故障的電力系統隨機優化調度（Stochastic Optimal Dispatch of Power System Considering Uncertain Line Failures under Extreme Weather Disaster）［D］.長沙：長沙理工大學電氣與信息工程學院（Changsha：School of Electrical and Information Engineering，Changsha Uni?versity of Science&Technology），2011.

［18］Q/CSG 11104002—2012，南方電網運行安全風險量化評估技術規范［S］.

［19］劉怡芳，張步涵，李俊芳，等（Liu Yifang，Zhang Buhan，Li Junfang，et al）.考慮電網靜態安全風險的隨機潮流計算（Probabilistic load flow algorithm considering static security risk of the power system）［J］.中國電機工程學報（Proceedings of the CSEE），2011，31（1）：59-64.

［20］高立志（Gao Lizhi）.考慮風電場間歇性的電力系統風險評估（Power System Risk Assessment Considering Wind Farm Intermittency）［D］.北京：北京交通大學電氣工程學院（Beijing：School of Electrical Engineering，Beijing Jiaotong University），2012.

［21］王紅印，張明亮，孫素琴，等（Wang Hongyin，Zhang Min?gliang，Sun Suqin，et al）.基于風險定量分析的電壓安全評估方法（Research on voltage security evaluation meth?od based on risk quantitative analysis）［J］.電網技術（Pow?er System Technology），2007，31（S2）：98-102.

［22］Coello C A C，Pulido G T，Lechuga M S.Handling multi?ple objectives with particle swarm optimization［J］.IEEE Trans on Evolutionary Computation，2004，8（3）：256-279.

［23］彭春華，孫惠娟（Peng Chunhua，Sun Huijuan）.基于非劣排序微分進化的多目標優化發電調度（Multi-objective optimization power dispatch based on non-dominated sort?ing differential evolution）［J］.中國電機工程學報（Pro?ceedings of the CSEE），2009，29（34）：71-76.

李燦（1990—），男，碩士研究生，研究方向為電力系統優化運行。Email：215638621@qq.com

曾沅（1975—），男，博士，副教授，研究方向為電力系統安全性與穩定性、電力系統規劃、電力系統優化運行。Email：zengyuan@tju.edu.cn

秦超（1986—），男，博士，講師，研究方向為電力系統風險評估。Email：chaoqin@tju.edu.cn

中圖分類號：TM73

文獻標志碼：A

文章編號：1003-8930（2016）06-0073-07

DOI：10.3969/j.issn.1003-8930.2016.06.013

作者簡介：

收稿日期：2015-11-13；修回日期：2015-12-28

Optimization Method for Power System Dispatching Considering Operation Risk

LI Can1，ZENG Yuan1，QIN Chao1，SONG Yunting2，JI Ping2，WU Wei3
（1.Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China；2.China Elctric Power Research Institute，Beijing 100192，China；3.State Grid Fujian Electric Power Co.，Ltd.，Economic and Technology Institute，Fuzhou 350012，China）

Abstract：In view of the situation that the consideration of risk factors in the existing optimal dispatch methods is too sin?gle and one-sided，the entire operation risk of the system is measured by branch overload and node voltage violation of limit，and a model based on operation risk is formulated with operation risk and generation cost as objective functions，allowing for the influence of wind power fluctuation，unit outage，line fault，load fluctuation and other uncertain factors. In this model，the stochastic load flow theory is introduced into the optimal dispatch to deal with the effect of many un?certainties on the operation risk with its Macro statistical properties，and for different weather conditions，the line fault probability is under real-time correction to get closer to the actual operating environment.This model is solved by the multi-objective particle swarm algorithm and the fuzzy set theory to seek a balance between economy and security.The IEEE-14 system is used to test the model and the results show that it is able to deal with the impact of uncertainties on the operation risk and reflect the difference of the dispatch scheme under different weather conditions which can provide a reference for the practical short-term optimal dispatch.

Key words：optimal dispatch；operation risk；uncertainties；stochastic load flow