中國碳市場統一價格指數編制研究

王文舉 ，李　峰

(首都經濟貿易大學 a.經濟學院；b.工商管理學院，北京 100070)

?

中國碳市場統一價格指數編制研究

王文舉a，李峰b

(首都經濟貿易大學 a.經濟學院；b.工商管理學院，北京 100070)

摘要：中國7個試點碳市場已全部啟動交易，編制統一價格指數是測度中國碳市場整體發展趨勢的重要手段，也是試點碳市場機制完善和統一碳市場建設的重要參考。研究發現，由于各試點碳市場交易量波動較大，簡單價格指數編制方法中的Carli指數編制方法更適合于當前中國碳市場統一價格指數的編制；隨著碳市場的不斷發展，可采用綜合價格指數編制方法中的Paasche指數編制方法對中國碳市場統一價格指數進行編制。研究還發現，以特定時期各試點碳市場配額交易量或交易金額占總體比例作為權數，有利于提升統一價格指數的穩定性。

關鍵詞：碳市場；統一價格指數；編制方法；簡單價格指數；綜合價格指數

引　言

越來越多的國家和地區正在運用市場機制以較低成本實現溫室氣體排放控制的目標。自2011年10月底，國家發展和改革委員會發布《關于開展碳排放權交易試點工作的通知》，正式批準在深圳、上海、北京、廣東、天津、湖北和重慶5市2省開展碳排放權交易試點。經過2年多的推進，2013年6月18日深圳市碳排放交易市場正式開市，成為國內首個啟動的試點碳市場。至2014年6月19日重慶市碳排放交易市場啟動交易，中國5市2省7個試點碳市場全部啟動交易。根據段茂盛和龐韜(2013)研究，碳排放權交易體系建設在本質上是對碳排放權的一種定價機制設計。如何對已試點碳市場價格動態變化進行測度，不僅受到研究人員的關注，也受到政府、企業、投資者和平常大眾的廣泛關注。

價格指數是對市場商品交易價格水平變化進行綜合測度的重要指標，也是研究市場商品交易價格變化程度和變化規律的關鍵變量。目前，中國還沒有政府機構公開發布碳市場統一價格指數。寧金彪和鐘青(2014)以各試點碳市場發放配額量占總配額量的比例作為權數，以2013年11月26日為基期，采用價格加權平均的方法編制了中國碳指數，從而對中國碳市場價格總體變化特征的綜合測度進行了有益的探索。不足之處在于：一是以2013年11月26日為基期，沒有考慮其他6個試點碳市場尚未啟動交易的現實；二是以各試點碳市場發放配額量占總配額量的比例作為權數，沒有考慮7個試點碳市場實際的碳排放權配額交易情況。基于此，本文以最后一個試點碳市場的啟動日期2014 年6 月19日為基期，對12種具有代表性的價格指數編制方法進行了理論和實證分析，從而為中國碳市場統一價格指數編制提供了理論基礎和現實依據。

一、價格指數編制方法歷史沿革

價格指數編制方法是在解決測度商品交易價格變動的現實中不斷發展和完善起來的，其理論流派和分類方法繁雜，目前還不存在統一的理論和一致的分類方法。根據杜金富等(2014)研究，雖然價格指數理論經歷長久的歷史變遷而產生了各種各樣的編制方法，但主要遵循著指數權數的選擇及指數形式的確定這兩大問題而展開，并按照歷史沿革和權數選擇將指數分為第一代指數和第二代指數[1]；楊緒忠和張玉玲(2007)同樣按照是否使用權數將指數分為綜合指數和平均數指數[2]；徐國祥等(2011)也按照是否使用權數將指數編制方法分為簡單指數法和加權指數法[3]。借鑒上述研究，參照孫清巖(2010)所采用的歷史沿革思路[4]，本文將價格指數分為簡單價格指數和綜合價格指數兩類進行研究。

(一)簡單價格指數

簡單價格指數通常被定義為不使用權數編制的價格指數，其實質是強調只針對商品交易價格變化而較少考慮甚或不考慮商品交易數量變化的一種指數編制方法。從價格指數編制的歷史沿革來看，早期的價格指數大部分屬于此種類型。其中，較有代表性的簡單價格指數包括：1738年法國經濟學家Dutot提出的一個簡單匯總物價指數，簡稱Dutot指數；1764年意大利經濟學家Carli提出的一個簡單算術平均指數，簡稱Carli指數；1863年英國著名經濟學家Jevons提出的一個簡單幾何平均指數，簡稱Jevons指數。假設有i=1,2,…,n個商品，0為基期，t為報告期，Dutot指數可以表示為：

(1)

Carli指數可以表示為：

(2)

Jevons指數可以表示為：

(3)

可以看出，Dutot指數編制方法是通過報告期的商品交易平均價格與基期的商品交易平均價格之比來計算價格指數，而Carli指數編制方法是通過計算單個商品價格指數的平均數來計算價格指數。杜金富等(2014)將前者稱之為價格法，而將后者稱之為指數法，其中，指數法因為是先計算各商品價格指數，再對各商品價格指數進行平均，能夠保證價格指數變化與商品實際價格變化方向始終一致，因此相對于價格法更為可取[1]。Jevons指數雖然采取的是幾何平均的方法，但形式上依然屬于指數法。

上述三種簡單價格指數的共同特征是僅考慮商品交易價格數據而未考慮商品交易數量資料，從而忽略了不同商品在經濟生活中的不同地位和重要性，缺乏充分的經濟內涵。基于此，一些經濟學家和相關學者通過加入商品交易數量資料，對上述簡單價格指數進行了完善和發展，其中，較有代表性的經過完善的簡單價格指數包括：1812年英國經濟學家Young提出的一個簡單加權平均指數，簡稱Young指數；1871年德國數學家Drobish提出的另一個簡單加權平均指數，簡稱Drobish簡單指數；1936年芬蘭經濟學家Tornqvist提出的對報告期和基期價格比進行加權幾何平均計算的價格指數，1967年荷蘭經濟學家Theil也提出同樣計算方法的指數，簡稱T-T指數。其中，Young指數可以表示為：

(4)

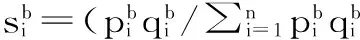
(5)

可見，Drobish簡單指數是在計算各商品交易價格指數基礎上，對各商品按照基期和報告期的交易數量賦予一定的權數進行加總，同樣考慮了各商品的市場地位和重要性。T-T指數可以表示為：

(6)

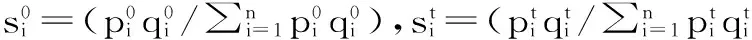
(二)綜合價格指數

綜合價格指數是指綜合考慮商品交易價格和商品交易數量共同變化特性而編制的一種價格指數，其與簡單價格指數最大的區別是，綜合價格指數加入了基于商品交易數量計算所得權數；與經過完善的簡單價格指數最大的區別是，綜合價格指數將商品交易數量看作同度量因素，從而不僅解決了不同計量單位的個體不能直接相加總的問題，客觀上也起到了權重的作用。從價格指數編制的歷史沿革來看，后期的價格指數大部分屬于此種類型。其中，較有代表性的綜合價格指數包括：1871年德國統計學家Laspeyres提出的以基期的商品交易數量作為權數計算的價格指數，簡稱Laspeyres指數；1874年，德國的另一個統計學家Paasche提出的將同度量因素固定在報告期，并用報告期商品交易數量作為權數計算的價格指數，簡稱Paasche指數。同樣，假設有i=1,2,…,n個商品，0為基期，t為報告期，則Laspeyres指數可以表示為：

(7)

Paasche指數可以表示為：

(8)

可見，Laspeyres指數將同度量因素確定為基期商品交易數量，其經濟內涵是指以基期商品交易數量作為權數，計算商品交易價格變化所帶來的報告期所需支付商品交易金額的相對變化；Paasche指數是將同度量因素確定為報告期商品交易數量，其經濟內涵是指以報告期商品交易數量作為權數，計算商品交易價格變化所帶來的報告期所需支付商品交易金額的相對變化。綜合來看，Laspeyres指數和Paasche指數的共同特征是先通過引入同度量因素進行綜合，然后再進行對比。除了以基期和報告期商品交易數量作為同度量因素外，還可以選擇其他同度量因素作為權數來計算統一價格指數。其中，較有代表性的綜合價格指數包括：1887年英國經濟學家Edgeworth和Mashall提出的以基期和報告期商品交易數量的簡單算術平均作為權數計算的加權綜合價格指數，簡稱E-M指數；1901年美國經濟學家Walsh提出，以基期和報告期商品交易數量的簡單幾何平均數作為權數計算的加權綜合價格指數，簡稱Walsh指數。其中，E-M指數可以表示為：

(9)

Walsh指數可以表示為：

(10)

可見，E-M指數將同度量因素確定為基期商品交易數量和報告期商品交易數量的算術平均數量，其經濟內涵是指以基期商品交易數量和報告期商品交易數量的算術平均數量作為權數，計算商品交易價格變化所帶來的報告期所需支付商品交易金額的相對變化；Walsh指數是將同度量因素確定為基期商品交易數量和報告期商品交易數量的幾何平均數量，其經濟內涵是指以基期商品交易數量和報告期商品交易數量的幾何平均數量作為權數，計算商品交易價格變化所帶來的報告期所需支付商品交易金額的相對變化。綜合來看，E-M指數和Walsh指數在同度量因素選擇是同時考慮了基期和報告期商品交易數量對報告期所需支付商品交易金額的相對變化的影響。除了E-M指數和Walsh指數外，還有通過直接對Laspeyres指數和Paasche指數進行再平均的辦法來綜合考慮基期和報告期商品交易數量對報告期所需支付商品交易金額的相對變化的影響。其中，較有代表性的綜合價格指數包括：1871年德國數學家Drobish提出的另一個先計算以基期數量加權的價格指數，再計算以報告期數量加權的價格指數，最后取兩者的簡單算術平均數為最終的價格指數，即取Laspeyres指數和Paasche指數簡單算術平均數的綜合價格指數，簡稱Drobish綜合指數；1899年英國經濟學家Bowley和1912年英國經濟學家Pigou先后提出應以拉式指數和派式指數的簡單幾何平均方法計算的價格指數，這一指數于1927年被美國經濟學家Fisher在其著作《指數的編制》中檢驗為是最好的指數，即理想指數，簡稱Fisher指數。其中，Drobish綜合指數可以表示為：

(11)

Fisher指數可以表示為：

(12)

可見，Drobish綜合指數和Fisher指數都是以Laspeyres指數和Paasche指數為基礎對綜合價格指數的發展。綜合來看，根據孫清巖(2010)關于型交叉價格指數和權交叉價格指數的定義[4]，上述6種綜合價格指數大致可以分為三類，其中，Laspeyres指數和Paasche指數為基礎綜合價格指數；E-M指數和Walsh指數為對Laspeyres指數和Paasche指數進行權數改造的綜合價格指數，可以稱之為權交叉綜合價格指數；Drobish綜合指數和Fisher指數為對Laspeyres指數和Paasche指數進行再平均形式的綜合價格指數，可以稱之為型交叉綜合價格指數。

二、價格指數編制方法實證分析

(一)數據來源與說明

為了分析前述各種不同的價格指數編制方法在編制中國碳市場統一價格指數中的差異，并最終選擇合適的方法，本文進行了廣泛的實證研究，共編制了12種中國碳市場統一價格指數。*實證的原始數據來源于中國碳排放交易網：http://www.tanpaifang.com/。考慮中國碳市場統一價格指數需要綜合反映深圳、上海、北京、廣東、天津、湖北和重慶7個試點碳市場價格波動情況，因此實證的起始時間為2014年6月19日，即最后一個試點碳市場——重慶市碳排放交易市場的開市時間，截至時間為2015 年12月31 日。由于各試點碳市場均存在沒有交易量的交易日，實證中以月度作為時間單位，基期為2014年6月，研究期間為2014年6月至2015年12月。需要說明的是，除了重慶試點碳市場絕大多數月份無成交量外，上海試點碳市場也存在2個沒有成交量的月份，對于沒有成交量月份的成交均價按照上一個有成交量交易日成交均價計算，這一處理方法在一般價格指數編制中被普遍采用。

(二)簡單價格指數方法實證分析

根據前述(1)～(6)式的6種簡單價格指數編制方法計算公式，基于中國7個試點碳市場數據，可計算6種簡單的中國碳市場統一價格指數變動情況，如表1所示。可以看出，無論是基于價格法編制的Dutot指數和Drobish簡單指數，還是基于指數法編制的Carli指數、Jevons指數、Yong指數和T-T指數，中國碳市場統一價格指數均存在明顯的下降趨勢。其中，Jevons指數下降幅度最大，達到50%以上，其次是Dutot指數、Carli指數、Yong指數和Drobish簡單指數，下降幅度也接近50%；T-T指數下降幅度最小，僅為40%左右。杜金富等(2014)研究指出，早期的簡單價格指數，Dutot指數一般情況下會大于或小于Jevons指數，但通常小于Carli指數，Carli指數大于等于Jevons指數[1]。與杜金富等(2014)的研究結論一致，中國碳市場Carli指數不僅明顯大于Jevons指數，同樣明顯大于Dutot指數。2015年6月后中國碳市場Dutot指數明顯大于Jevons指數，在此之前的大部分時間，Jevons指數大于Dutot指數。優化的簡單價格指數，T-T指數明顯大于Yong指數，而Yong指數則明顯大于Drobish簡單指數。綜合來看，早期簡單價格指數與優化的簡單價格指數之間并不存在明顯的數值上的大小關系，各簡單價格指數在數值大小上存在顯著差異。

表1

截至2015年12月末中國碳市場6種簡單價格指數變動情況

從表1還可以看出，早期的3個簡單價格指數中， Carli指數均值最大，標準差最小，通過標準差與均值之比計算所得的變異系數最小，僅為0.21； Jevons指數均值最小，標準差最大，通過標準差與均值之比計算所得的變異系數最大，為0.24。優化的3個簡單價格指數中， T-T指數均值最高，變異系數最低，僅為0.20；而Yong指數和Drobish簡單指數均值相對較低，而變異系數相對較高，均為0.23。綜合來看，Carli指數、Jevons指數、T-T指數和Yong指數均屬于基于指數法編制的價格指數，但各價格指數的變異系數存在顯著差異。將變異系數看作價格指數穩定性測度指標，基于價格法還是基于指數法并非價格指數穩定性的決定因素。同樣，Jevons指數和T-T指數同屬于基于幾何平均法計算所得的指數，兩者的變異系數也存在顯著差異，基于算術平均還是基于幾何平均編制也并非指數穩定性的決定因素。從價格指數穩定性角度看，早期簡單價格指數中的Carli指數編制方法和優化簡單價格指數中的T-T指數編制方法更適合作為中國碳市場統一價格指數編制方法。

(三)綜合價格指數方法實證分析

根據前述(7)～(12)式的6種綜合價格指數編制方法的計算公式，基于中國7個試點碳市場數據，可計算6種綜合的中國碳市場統一價格指數變動情況，如下頁表2所示。可以看出，兩個基礎綜合價格指數、兩個權交叉綜合價格指數和兩個型交叉綜合價格指數均顯示中國碳市場統一價格指數呈明顯的下降趨勢。其中，Laspeyres指數和E-M指數下降幅度較大，接近50%；其次是Walsh指數、Drobish綜合指數和Fisher指數，下降幅度接近40%；Paasche指數下降幅度最小，僅為25%左右。這也表明在大多數月份中，Laspeyres指數和E-M指數大致相近，但要小于Walsh指數、Drobish綜合指數和Fisher指數；Walsh指數、Drobish綜合指數和Fisher指數大致相近，但要小于Paasche指數。價格指數大小一直是價格指數編制方法爭論的一個重要領域，根據李豐(1995)研究，通常經驗表明Laspeyres指數大于Paasche指數[5]。但表2中基于Paasche指數編制方法編制的中國碳市場統一價格指數明顯大于基于其他指數編制的中國碳市場統一價格指數。可見，Laspeyres指數也不是必然大于Paasche指數，從數學上來講，Paasche指數可以小于、等于或大于Laspeyres指數。

除對Laspeyres指數和Paasche指數孰大孰小之爭外，理論界還一直存在著對Laspeyres指數和Paasche指數孰優孰劣之爭，孰大孰小之爭也是孰優孰劣之爭的依據。孫慧釣和孫桂娟(1996)基于方差和變異系數對Laspeyres指數和Paasche指數進行了研究，發現當Laspeyres指數大于Paasche指數，Laspeyres指數所對應的方差和變異系數也同時大于Paasche指數所對應的方差和變異系數，此時用Laspeyres指數反映商品價格變化一般程度上要強于Paasche指數；反之同樣成立[6]。

如表2所示，基于Paasche指數計算所得的中國碳市場統一價格指數在更多的月份上大于基于Laspeyres指數計算所得，因此，使用Paasche指數編制法編制中國碳市場統一價格指數能夠更好地反映中國碳市場配額交易價格變化。同理，權交叉綜合價格指數中基于Walsh指數編制的中國碳市場統一價格指數在更多月份大于基于E-M指數編制的中國碳市場統一價格指數，使用Walsh指數編制法編制中國碳市場統一價格指數能夠更好地反映中國碳市場配額交易價格變化；型交叉綜合價格指數中基于Drobish綜合指數編制的中國碳市場統一價格指數在更多月份大于基于Fisher指數編制的中國碳市場統一價格指數，使用Drobish綜合指數編制法編制中國碳市場統一價格指數能夠更好地反映中國碳市場配額交易價格變化。

此外，從表2還可以看出，在兩個基礎綜合價格指數中， Paasche指數均值更大，變異系數更小；兩個權交叉綜合價格指數和兩個型交叉綜合價格指數均值基本相同，變異系數趨于一致，且變異系數要小于兩個基礎綜合價格指數的變異系數。可見，將變異系數看作指數穩定性測度指標，基礎綜合價格指數中的Paasche指數穩定性要強于Laspeyres指數，更適合于編制中國碳市場統一價格指數；使用其他兩個權交叉綜合價格指數和兩個型交叉綜合價格指數編制中國碳市場統一價格指數，在價格指數穩定性方面沒有明顯差異。

結　論

以變異系數作為價格指數穩定性測度指標，簡單價格指數中的Carli指數和T-T指數編制方法更加適合作為中國碳市場統一價格指數編制方法；綜合價格指數中的Paasche指數、Walsh指數和Drobish綜合指數也都適合作為中國碳市場統一價格指數編制方法。考慮到中國7個試點碳市場成交量具有明顯的不連續性和波動性特征，將Carli指數的權重設置為各試點碳市場報告期成交金額，將Young指數和T-T指數固定參考期各試點碳市場成交金額權重轉換為報告期，重新計算所得的修正的Carli指數和Young指數的變異系數僅為0.11，要遠低于基于原來簡單價格指數的變異系數；同樣，重新計算的T-T指數的變異系數為0.15，也遠低于基于原來簡單價格指數的變異系數；前者的變異系數要明顯小于后者，表明前者更適合作為中國碳市場統一價格指數的編制方法。以2014年6月至2015年12月各試點碳市場成交金額占總體成交金額的比重作為權數，計算所得的中國碳市場統一價格指數具有更高的穩定性。

表2　截至2015年12月底中國碳市場6種綜合價格指數變動情況

綜合來看， 由于啟動時間較短且成交量波動較大， 當前中國碳市場統一價格指數適合采用指數法編制的以較長時間各試點碳市場成交金額占總體成交金額比重作為權數的簡單價格指數法來進行編制， 以修正的Carli指數和Young指數為代表， 可以保證價格指數的穩定性； 隨著各試點碳市場的發展和成交量的穩定， 中國碳市場統一價格指數適合采用以報告期成交量為權數的綜合價格指數法來進行編制， 以Paasche指數為代表， 可以更好地反映市場真實的交易情況； 在適當的時候采用對Laspeyres指數和Paasche指數進行調整的型交叉綜合價格指數來進行編制， 以Fisher指數為代表， 可以保留理想指數的良好特性。

參考文獻：

[1]杜金富，等. 價格指數理論與實務[M].北京：中國金融出版社，2014.

[2]楊緒忠, 張玉玲. 論綜合指數和平均數指數[J].統計與信息論壇, 2007，(11): 19-22.

[3]徐國祥，等. 統計指數理論、方法與應用研究[M].上海：上海人民出版社，2011.

[4]孫清巖. 股票價格指數編制：理論、方法與創新[M].大連：東北財經大學出版社，2010.

[5]李豐. L氏指數與P氏指數之差的經濟學意義[J]. 統計研究，1995, (5): 46-49.

[6]孫慧釣, 孫桂娟. Laspeyres指數與Paasche指數的比較[J]. 財經問題研究, 1996，(10): 57-58.

[責任編輯：房宏琳，曾博]

收稿日期：2016-03-16

基金項目：國家社會科學基金重大項目“中國碳市場成熟度、市場機制完善及環境監管政策研究”(14ZDA072)；北京市屬高等學校高層次人才引進與培養“長城學者”計劃資助項目“碳排放與博弈計量研究”(CIT&TCD20140321)；中國博士后科學基金第59 批面上項目“中國碳市場發展對產業競爭力的影響研究”(2016M591204)

作者簡介：王文舉(1965—)，男，副校長，教授，博士生導師，從事博弈論與計量經濟學研究；李峰(1979—)，男，通訊作者，博士后流動站研究人員，從事博弈論與計量經濟學研究。

中圖分類號：F222.1

文獻標志碼：A

文章編號：1002-462X(2016)07-0132-06