滬深300股指期權定價實證分析

□文/黃 瑞

（安徽財經大學金融學院 安徽·蚌埠）

?

滬深300股指期權定價實證分析

□文/黃 瑞

（安徽財經大學金融學院 安徽·蚌埠）

［提要］ 針對滬深300股指期權定價問題，分別基于B-S-M模型、二叉樹模型和蒙特卡洛模擬方法為期權定價。通過建立G A RCH模型估計出標的資產的時變波動率，對滬深300股指期權合約進行實證分析，得到2016年5月到期的期權合約在2016年4月1日到15日交易的理論價格，最后將各模型的實證結果進行對比。結果表明：二叉樹模型和蒙特卡洛模擬得到的理論價格更接近仿真交易的市場價格。

關鍵詞：期權定價；B-S-M模型；二叉樹；蒙特卡洛模擬

收錄日期：2016年6月15日

近年來，我國資本市場發展迅速，市值規模已躍居全球第二位，但產品結構單一問題仍較為突出。在該背景下，2013年11月8日中國金融期貨交易所推出滬深300股指期權合約的仿真交易。2015年2月9日，上海證券交易所正式上市我國首個場內期權產品——上證50ETF期權，開啟了中國證券市場的期權時代。期權、期貨等金融衍生產品的交易通常有套期保值、投機、套利和資產管理四大目的，不同于同時轉移不利風險和有利風險的期貨，期權多頭在運用期權進行套期保值時，能夠只把不利風險轉移出去而把有利風險留下，這種特征為期權帶來很大的金融市場，具有巨大的發展潛力。在可預見的未來，滬深300股指期權等期權品種將更為豐富。對期權定價的研究具有重要意義。鑒于此，本文較為系統地研究了基于GARCH模型求得波動率參數前提下，B-S-M模型、二叉樹和蒙特卡洛模擬對滬深300股指期權的定價問題。

一、理論模型

（一）B-S-M模型。BS模型假設標的資產價格呈幾何布朗運動，其價格變動連續，其波動率和無風險利率已知且保持恒定，標的資產在期權合約期內無紅利支付，市場無交易成本并且允許做空。

假設股票價格S遵循幾何布朗運動，標的資產價格服從對數正態分布，所以T時刻標的指數的對數價格服從正態分布，在風險中性世界下，看漲期權的價值c為：

對上式的積分過程進行求解，結果為：

表1 收益率序列的基本統計特征

B-S-M模型 二叉樹模型 蒙特卡洛模擬日期模型c p c p c p 4月1日4月5日4月6日4月7日4月8日4月11日4月12日4月13日4月14日4月15日平均誤差245.4081 268.2539 260.6854 219.8066 204.5708 231.6011 221.1690 251.2518 261.7305 255.5217 7.63416 61.1072 42.3642 42.0086 49.6227 58.1998 41.6190 43.0898 30.4956 26.7773 24.4416 46.6874 245.7281 268.3271 260.8700 220.1248 205.1496 232.1032 221.0372 251.0135 262.1054 255.2704 7.62683 61.7679 42.7004 42.4098 50.2174 59.1141 42.3434 43.2307 30.4500 27.2903 24.2998 46.27761 244.8107 266.1549 250.5930 219.2648 205.0415 230.7392 221.4350 251.7891 261.5108 255.1193 7.33899 61.1506 42.3578 44.9707 50.3060 58.0638 41.7757 42.7180 30.4238 26.4183 24.6168 46.37987

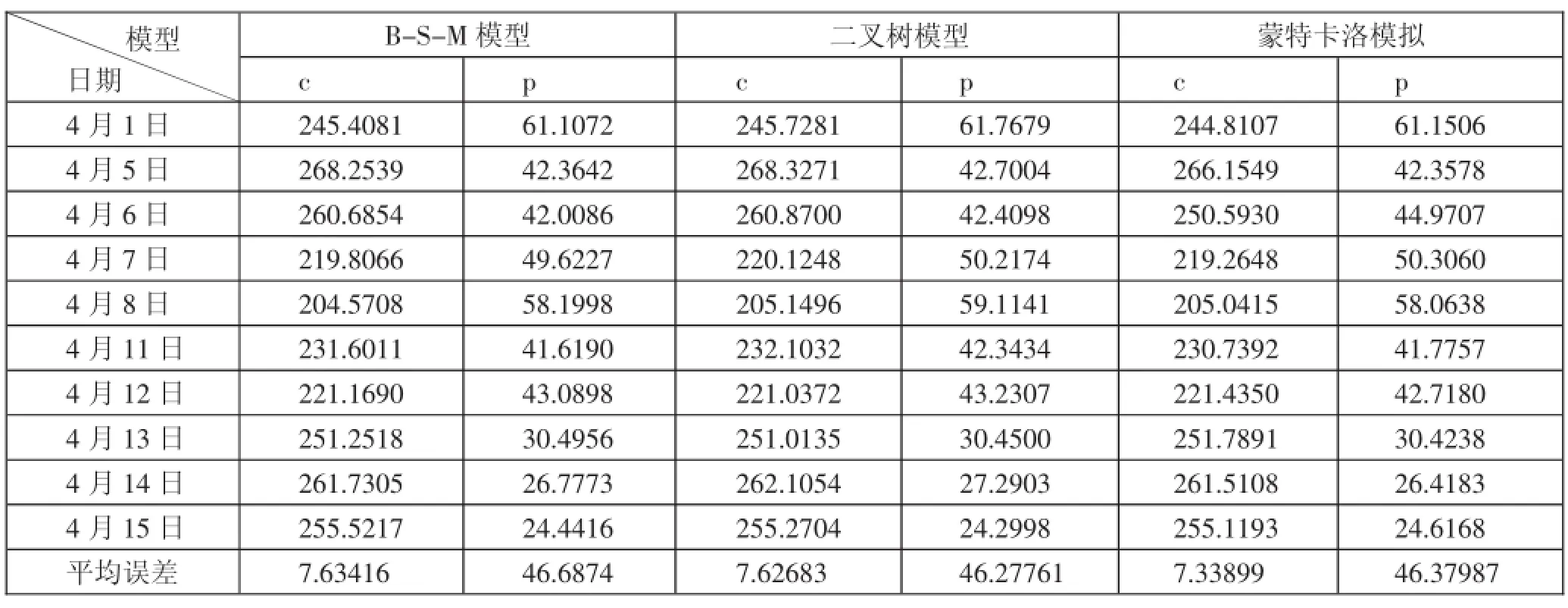
表2 IO 1605-c（p）-3050期權定價結果

（二）二叉樹模型。二叉樹定價模型假設標的資產的價格在dt時間段后從開始的S變動到Su或者Sd，并且假定在整個期權的合約期內標的資產價格每次漲價或跌價的概率和幅度不變。模型將整個合約期分為若干時間段，根據標的資產的歷史波動率模擬標的資產價格所有可能的發展路徑，對每一路徑上的每一節點計算期權的價值，從而貼現倒推出期權現值。相較于B-S公式，二叉樹模型適用于處理更為復雜的期權。

（三）蒙特卡洛模擬。蒙特卡洛模擬是一種基于模擬標的資產價格的隨機運動路徑得到期權價值期望值的數值方法。基本思路為：歐式期權的價值等于期權到期回報的期望值的貼現（式（1）），因此先模擬出風險中性世界下標的資產價格的運動路徑，然后計算所有路徑結果下期權回報的均值，最后用無風險利率貼現得到期權價值。

假定標的資產價格服從對數正態分布，則經過dt時間段后標的資產的價格為：

可由（3）式產生標的資產價格的運動路徑，模擬得到T時刻標的資產的價格。求得T時刻的每個標的資產的價格對應的看漲或看跌期權在T時刻的價值，即：cT=max（ST-K，0），pT= max（K-ST，0）。據此可求得T時刻期權價值的期望值，對期權價值的期望值貼現進而計算出期權定價。

（四）波動率的估計模型。上述模型需要事先已知一個重要的參數——波動率σ。金融時間序列常常具有條件異方差性，GARCH模型考慮到波動的自相關和均值回復的特性，能更好地描述時變的波動率。GARCH（p，q）模型的具體形式為：，其中Rt是標的資產在t時刻的收益率，σ是t時刻方差的估計值，μ為收益率的均值，假定殘差εt服從正態分布或者t分布。

為了統一單位，需要將收益率的日標準差轉化為年化標準差：

二、實證分析

（一）數據的選取和描述統計。本文選取滬深300指數日收盤價作為標的資產的數據，對滬深300股指期權的合約價值進行估計。數據均來源于WIND資訊金融終端。選擇2016年3月SHIBOR的均值為R＝3.08%，根據1+R＝er，轉換得到其連續復利利率作為無風險收益率r＝3.04%。數據的時間跨度為2015 年4月1日到2016年4月15日，共計256組日交易數據。取對數作差分形式對日收益率數據進行處理，計算公式為：Rt=ln （Pt/Pt-1），其中Rt表示t時刻樣本的對數收益率；Pt表示t時刻樣本的收盤價。

對收益率序列進行相應的統計描述。給出標的資產收益率的描述性統計量如表1所示。（表1）

（二）數據的檢驗和模型的估計。首先，采用ADF檢驗法，對滬深300指數進行單位根檢驗。檢驗結果表明，在1%的顯著性水平下，樣本收益率序列的ADF統計量為-14.79246，小于臨界值-3.45599，樣本收益率序列均平穩；其次，繪制樣本期內收益率的折線圖，發現收益率序列具有明顯的波動率聚集現象，表明誤差可能具有條件異方差性質。將收益率進行平方生成新序列，觀察新序列所有滯后階數的自相關和偏自相關系數均顯著不為0，Q統計量大于顯著性水平下的臨界值，表明收益率序列均存在ARCH效應。

對收益率分別嘗試建立殘差分別服從正態分布和t分布的GARCH（1，1）、GARCH（1，2）、GARCH（2，1）和GARCH （2，2）模型。根據AIC和SC準則，回歸結果表明殘差服從t分布的模型顯著優于其服從正態分布的模型，同時在殘差服從t分布的模型中，對收益率序列建立的GARCH（1，1）模型最優。因此，本文最終選用GARCH（1，1）-t模型對標的資產收益率建模。估計結果為：

ARCH和GARCH項系數之和均小于1，滿足參數約束條件。由MATLAB軟件導出t時刻對應的波動率σt，按照（4）式將其轉化為年化波動率用于定價。

（三）結果分析。運用B-S-M模型、二叉樹模型和蒙特卡洛模擬方法對IO1605-3050看漲和看跌期權定價。其中，二叉樹模型的區間步長為1天，蒙特卡洛模擬法對每日合約價格模擬出100，000條運動路徑。選取2016年4月1日至4月15日作為評價期間，運用這三個模型對這10天的期權進行定價。定價結果如表2所示。（表2）

假定仿真交易的數據是有效的，由表2可知，三種模型對于看漲期權的定價誤差較小，對于看跌期權的定價誤差較大，其中蒙特卡洛模擬較優，其次是二叉樹模型，B-S-M模型定價誤差較大。如果假定仿真交易數據是有效的，根據看漲期權合約定價誤差較小的結果，可知對無風險收益率的選擇是基本有效的，但是同樣的數據求得看跌期權合約的定價誤差較大，進一步套用看漲看跌平價公式，發現仿真交易數據難以滿足看跌看漲平價定理，扣除交易費用后，套利機會依然存在。誤差可能是由于仿真交易市場不夠完善或者選取參數的誤差所致。

三、結論

本文基于M-B-S模型、二叉樹定價模型和蒙特卡洛模擬方法分別對滬深300股指期權進行定價，對資產收益率序列建立GARCH模型，選用時變波動率作為波動率參數。將定價結果與仿真交易數據進行比較，發現二叉樹模型和蒙特卡洛模擬方法較優，進一步計算發現仿真交易數據并不滿足期權看漲看跌平價定理，扣除交易費用后依然存在套利機會，說明仿真的期權市場需要進一步完善，以期為未來滬深300股指期權的推出奠定基礎。本文得到的定價結果表明，三種期權定價方法對看漲期權的定價誤差較小，說明模型是有效的。

主要參考文獻：

［1］張原錕，楊華.基于Bl ack-Schol es模型的滬深300股指期權定價研究［J］.北華大學學報，2014.15.1.

［2］鄭振龍，陳蓉.金融工程［M］.北京：高等教育出版社，2015.

中圖分類號：F830.91

文獻標識碼：A