風力發電機傳動系統故障診斷的機電仿真研究

時獻江，　房欽國，　趙曉文，　杜恒，　司俊山

(哈爾濱理工大學 機械動力工程學院，黑龍江 哈爾濱 150080)

?

風力發電機傳動系統故障診斷的機電仿真研究

時獻江，房欽國，趙曉文，杜恒，司俊山

(哈爾濱理工大學 機械動力工程學院，黑龍江 哈爾濱 150080)

摘要:為了研究風力發電機組傳動系統齒輪故障在發電機電流信號中的響應過程，擴展電流信號診斷方法的應用范圍。在考慮齒輪嚙合剛度變化和模擬斷齒故障變化特征的基礎上，建立齒輪副動力學模型；以典型的雙饋風力發電機為對象，建立雙饋發電機及其控制系統模型。利用齒輪副和發電機的轉速參數關聯兩個模型，構建機電聯合仿真模型。在理論上研究齒輪正常或存在斷齒時的電流故障特征，并與試驗臺模擬故障試驗比較。仿真與試驗結果表明，發電機定子電流可以準確反映齒輪的故障特征信息，且在離網狀態下，主要會引起電流信號的頻率調制特征。

關鍵詞:風力發電機；傳動系統；齒輪；定子電流；故障診斷;仿真

0引言

隨著風力發電技術的發展，以單體機組大型化、集中安裝和控制為特點的風電場成為主要發展方向[1]。隨著風力發電機組的保有量和在役運行時間的增長，其維修成本越來越大，據統計，目前風機的維護費用占總成本的25%～30%[2]。雖然大多數風場均配備較完善的數據采集與監控系統(supervisory control and data acquisition，SCADA)，但是其檢測參數多為溫度、電壓和電流等常規靜態檢測參數，缺乏振動等動態監控及診斷手段，主要原因是振動診斷傳感器成本高，安裝與信號傳輸不便。為此，本文探討一種利用發電機電信號(電壓、電流)進行機械故障診斷的間接診斷方法-電機電流信號分析法，也稱無傳感器診斷方法。

目前，國內外已有多篇關于該方法的報道，如國外學者Royo等建立了一個異步發電機系統的簡易模擬實驗臺，研究和分析了定子匝間短路和軸承故障的定子電流頻譜[3]。而馬宏忠等用分析雙饋異步發電機定子負序電流來確定定子繞組匝間短路故障的來源[4]。Yang Wenxian等建立了較完善的風力發電機組故障模擬試驗臺，采集發電機電流、電壓及功率參數，利用小波變換方法進行機組的機械故障診斷，證明了用電參數方法進行機械故障診斷方法的優點[5]。Amirat等采用定子電流的幅值解調法以及基于經驗模態分析方法進行風力發電機軸承故障診斷，取得了較好結果[6-7]。這些研究成果表明，電機電流信號分析法用在風力發電機故障診斷中是完全可行的。

但是，上述文獻多針對發電機本身的電氣或機械故障，對于傳動系統的機械故障診斷研究較少。而傳動系統故障診斷，比如齒輪箱故障診斷是風力發電機組監測與診斷工作中的極為重要一環。有文獻報道，一個大型風電機的齒輪箱更換工作就要花費上百萬元[2]。另外，由于風力發電機是一個機械結構和控制系統異常復雜的機電一體化產品，而且安裝環境較惡劣，直接以其為對象進行故障診斷研究較為困難[8]。因此，進行計算機模擬仿真和試驗臺模擬研究不失為一種捷徑。本文主要以典型的雙饋風力發電機(double fed induction generator，DFIG)傳動鏈中的齒輪故障診斷為對象，聯合發電機電氣仿真模型和齒輪傳動系統的機械動力學模型，通過仿真分析，在理論上探討無傳感器診斷方法的可行性，最后，通過自制的試驗臺進行了驗證分析。

1風力發電機的主要結構及組成

DFIG發電機是目前風力發電商業市場上的主力型式[1]。一個典型的DFIG風電機組的機械組成和控制系統如圖1所示，包括葉片、主軸和主軸承，增速齒輪箱和雙饋發電機等。發電機定子與電網直接連接，轉子通過兩個背靠背的交-直-交變頻器連接到電網中。當發電機轉子旋轉頻率fr2變化時，自動控制系統控制轉子勵磁頻率f2來保證定子輸出頻率f1與電網頻率相等，即

f1=pnfr2+f2。

(1)

式中pn為發電機的極對數。

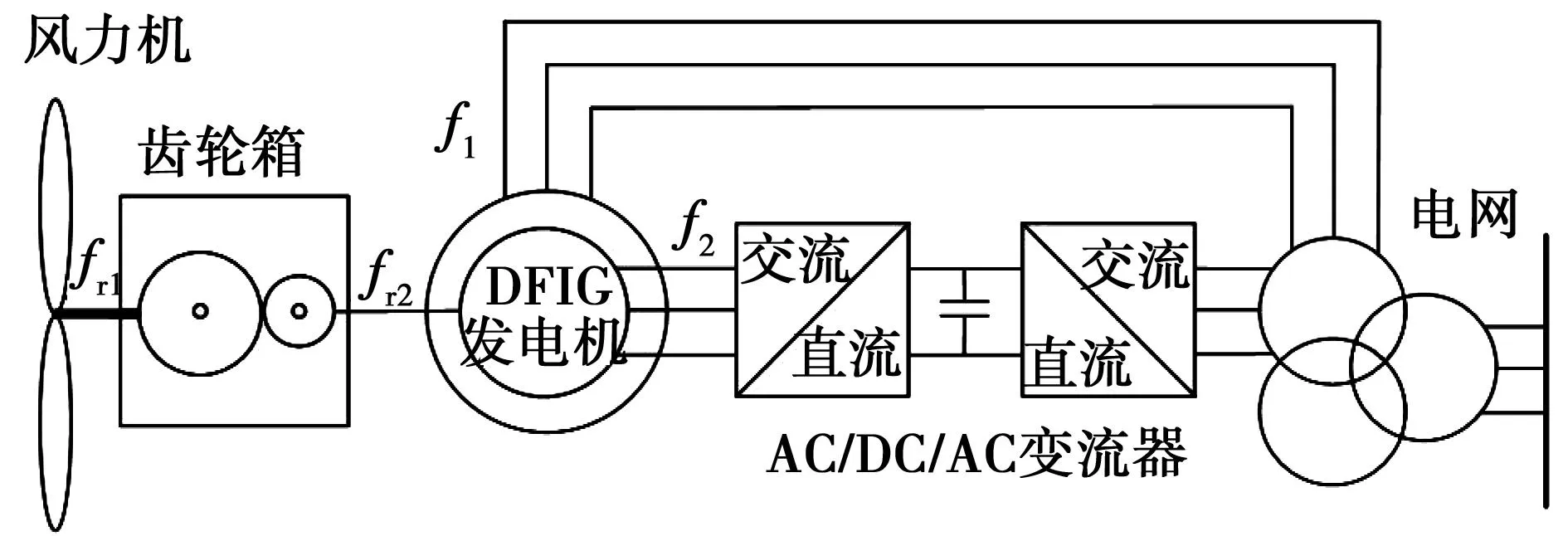
圖1　DFIG風力發電機組的基本組成Fig.1　Basic composition of DFIG wind turbine units

2雙饋風力發電機組數學模型

2.1交流異步風力發電機的數學模型

根據交流電機理論，異步發電機在d-q旋轉坐標系下的動態特性可由下述方程描述[9]:

電壓方程：

(2)

式中：usq，usd，isq和isd為定子電壓、電流矢量的d-q坐標分量；urq，urd，irq，ird為轉子電壓、電流矢量的d-q坐標分量；Rs，Rr為定子、轉子電阻；Ψsq,Ψrq,Ψsd和Ψrd為定、轉子磁鏈矢量的d-q坐標分量；ωs=ω1-ωr,為d-q坐標系相對于轉子的角速度，其中ω1，ωs為同步轉速和轉子電角速度；p為微分算子，p=d/dt。

磁鏈方程為：

(3)

式中：Ls，Lr和Lm為定子、轉子的自感以及互感。

根據異步電機電磁轉矩定義，可得d-q坐標系下異步發電機電磁轉矩Te方程為

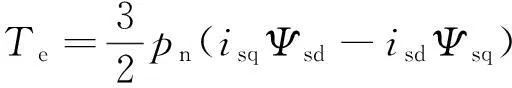
(4)

異步發電機的運動方程為

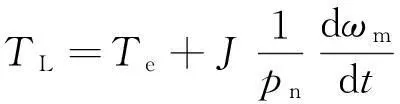
(5)

式中：TL為風力機提供的拖動轉矩；ωm為風力機提供的拖動轉速；J為系統的轉動慣量。

2.2風力發電機傳動齒輪副力學模型

由文獻[10]可知，圖2所示直齒輪傳動副的動力學微分方程為

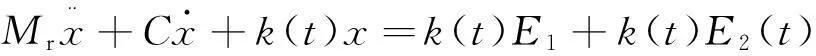
(6)

式中：x為沿作用線上齒輪的相對位移；C為齒輪嚙合阻尼；k(t)為齒輪嚙合剛度；Mr為兩齒輪的等效質量；E1為齒輪受載后的平均靜彈性變形；E2(t)為齒輪的誤差和故障造成的兩個齒輪間的相對位移。

其中Mr為

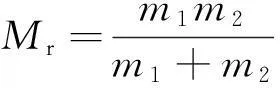
(7)

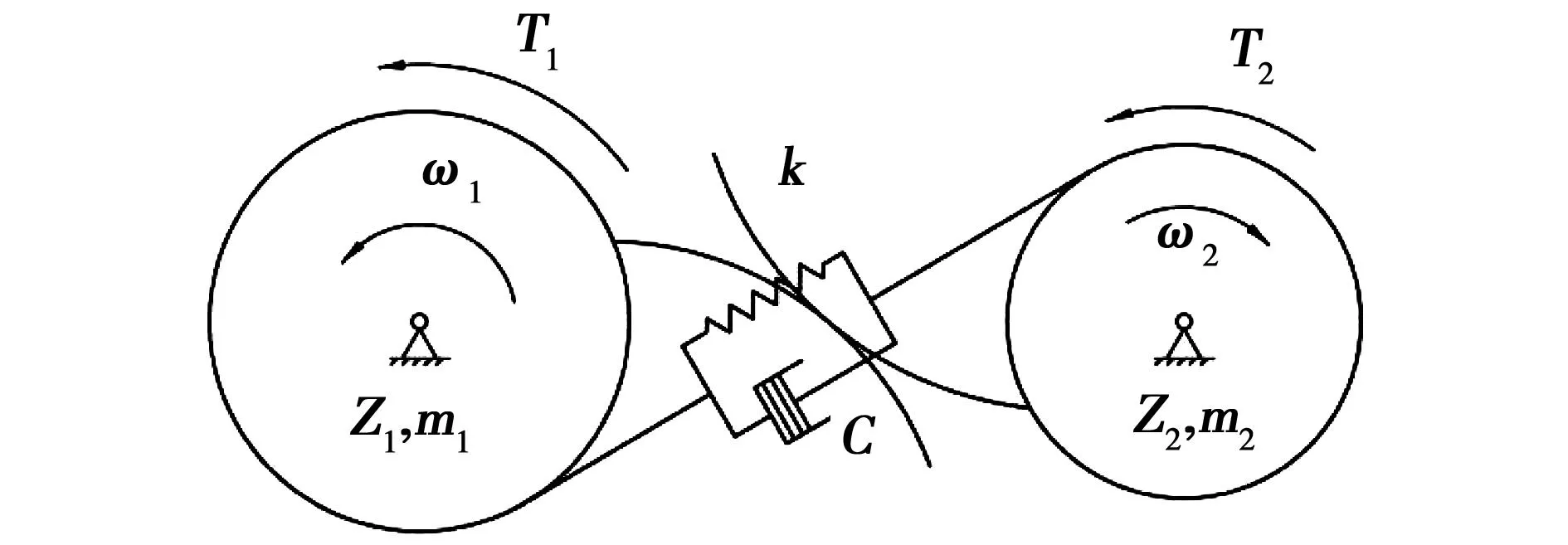
圖2　發電機傳動齒輪副的力學模型Fig.2　Mechanical model of generator drive gears

由式(6)可知，齒輪的振動為自激振動，該公式的左端代表齒輪副本身的振動特征，右端為激振力函數。由激振力函數可以看出，齒輪的振動來源于兩部分：其中一部分為k(t)E1，它是與齒輪的誤差和故障無關的常規振動，理想狀態下可以認為該項為0，此時式(6)簡化為：

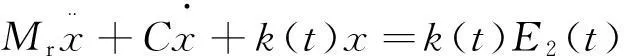
(8)

此時，激振力僅為另一部分k(t)E2(t)，這是一個調制信號，它取決于齒輪的綜合剛度和故障函數的變化過程。圖3為一個直齒輪的嚙合剛度k(t)的變化曲線，理想狀態下可近似認為是一個方波函數；E2(t)取決于齒輪的故障類型，假如出現斷齒故障時，E2(t)則以該齒輪的轉頻周期性出現。可以說齒輪的振動主要是由k(t)和E2(t)調制的這種周期性變化引起的。

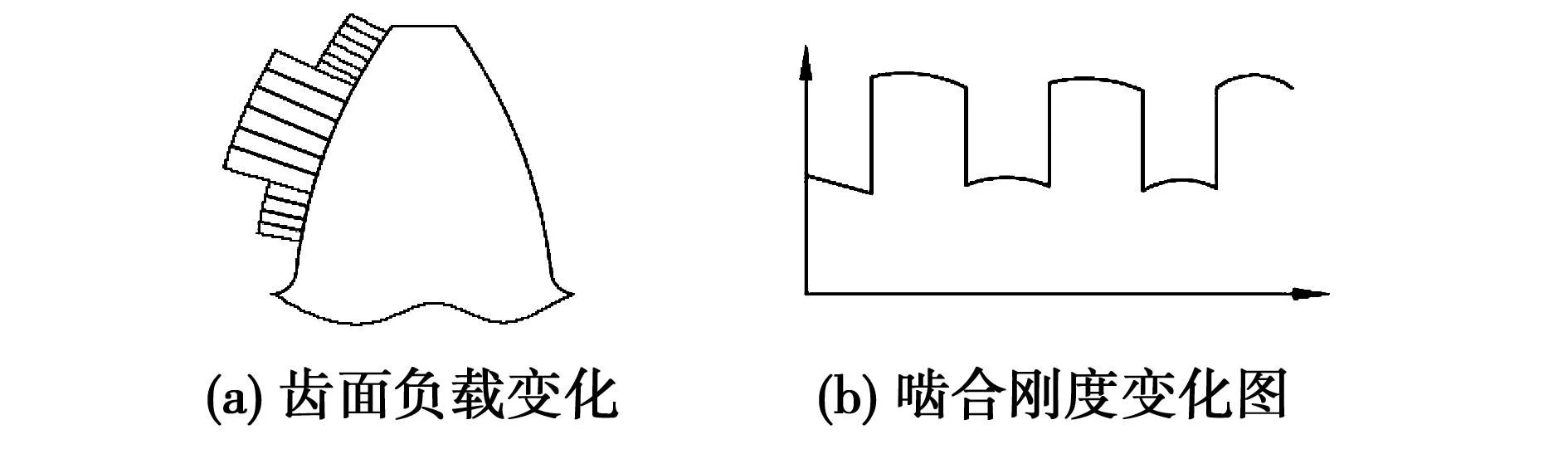
圖3　齒面載荷和剛度變化Fig.3　Tooth surface load and stiffness changes

3雙饋風力發電機組仿真模型

3.1風力發電機傳動齒輪副仿真模型

根據振動微分方程(8) 知，只要對輸出加速度作適當的二次積分則可求得相應的輸出位移響應。可利用SIMULINK的基本模塊庫建立仿真模型如圖4所示。由于發電機模型仿真時需要角速度輸入，所以抽出該模型的速度參量，除以齒輪半徑作為角速度波動輸出。該模型可封裝成一個子模塊Sub_Gear供調用。

圖4　發電機傳動齒輪副的力學仿真模型Fig.4　Mechanical simulation model of generator　　　drive gears

仿真時，假設大小齒輪的齒數為Z1=32，Z2=23，模數m=3，齒寬B=20，考慮電機質量時的等效質量Mr=4.5 kg，k=200～250 kN，C=300 N· s/m, 齒輪的嚙合阻尼

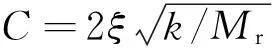
(9)式中：ξ為齒輪嚙合時的阻尼比,一般為0.03～0.17[9]；k為齒輪的平均嚙合剛度。系統受激振力為

F(t)=k(t)E2(t)=

10square(2πfzt)(1+sin(2πfr1t))。

(10)

式中：fz為齒輪嚙合頻率，等于嚙合剛度的變化頻率；fr1為故障齒輪軸的旋轉頻率。

3.2包含齒輪傳動副的雙饋風力發電機的機電仿真模型

交流雙饋發電機的機電仿真模型如圖5所示。仿真模型包括發電機模塊、發電機轉子變頻勵磁模塊、負載模塊、電參數測量模塊和齒輪故障模擬仿真子模塊(如圖4所示)。雙饋發電機模型由繞線式異步電動機模塊代替，設置成發電機運行方式。發電機的定子繞組接三相阻性負載，采用脈寬調制(pulse width modulation,PWM)功率變頻器模塊給發電機轉子單向勵磁供電，僅模擬離網工況。

仿真系統的基本參數為:發電機額定功率3 kW，額定電壓220 V AC，額定轉速1 400 rpm，極對數pn=2，定子電阻、電感Rs=1.918 8 Ω、Ls=0.241 22 H，折算到定子側的轉子電阻、電感Rr=2.571 2 Ω、Lr=0.241 22 H，定子、轉子互感Lm=0.234 H。參考坐標系取同步參考坐標系，初始狀態均為0。

發電機的機械輸入設為轉速輸入，取齒輪故障模擬仿真子模塊的輸出和一個平均轉速的疊加。由于齒輪故障模擬仿真子模塊的輸出僅為一個速度波動成分，所以需要加上平均速度值。

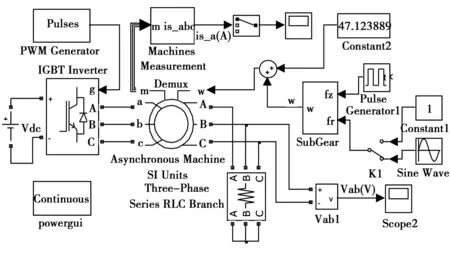
圖5　雙饋感應發電機及控制系統仿真模型Fig.5　DFIG and control system simulation model

4風力發電機組故障模擬實驗臺

模擬試驗臺的整體結構示意圖及實物圖片如圖6及圖7所示，由模擬風力發電機組(包括模擬風機的交流異步電動機，增速齒輪箱和DFIG發電機、發電機控制系統，以及數據采集系統和計算機組成。風機模擬電機采用1.5 kW的交流異步電機，變頻驅動；采用1.5 kW的繞線式三相異步電機作為雙饋感應發電機。兩臺電機的極對數均為3，電動機的額定轉速為920 rpm。由于實驗室的條件限制，并網控制存在一定的難度[11]，所以發電機的定子繞組僅與三相阻性負載連接，離網運行。采用的三相變頻器輸出不同頻率的100 V的轉子相電壓，單向給轉子繞組勵磁，僅模擬發電機的同步和次同步運行狀態。采用齒輪對模擬風力發電機組的增速箱，其中電動機端齒輪齒數為34，發電機端齒輪齒數為23，增速比約為1.478。

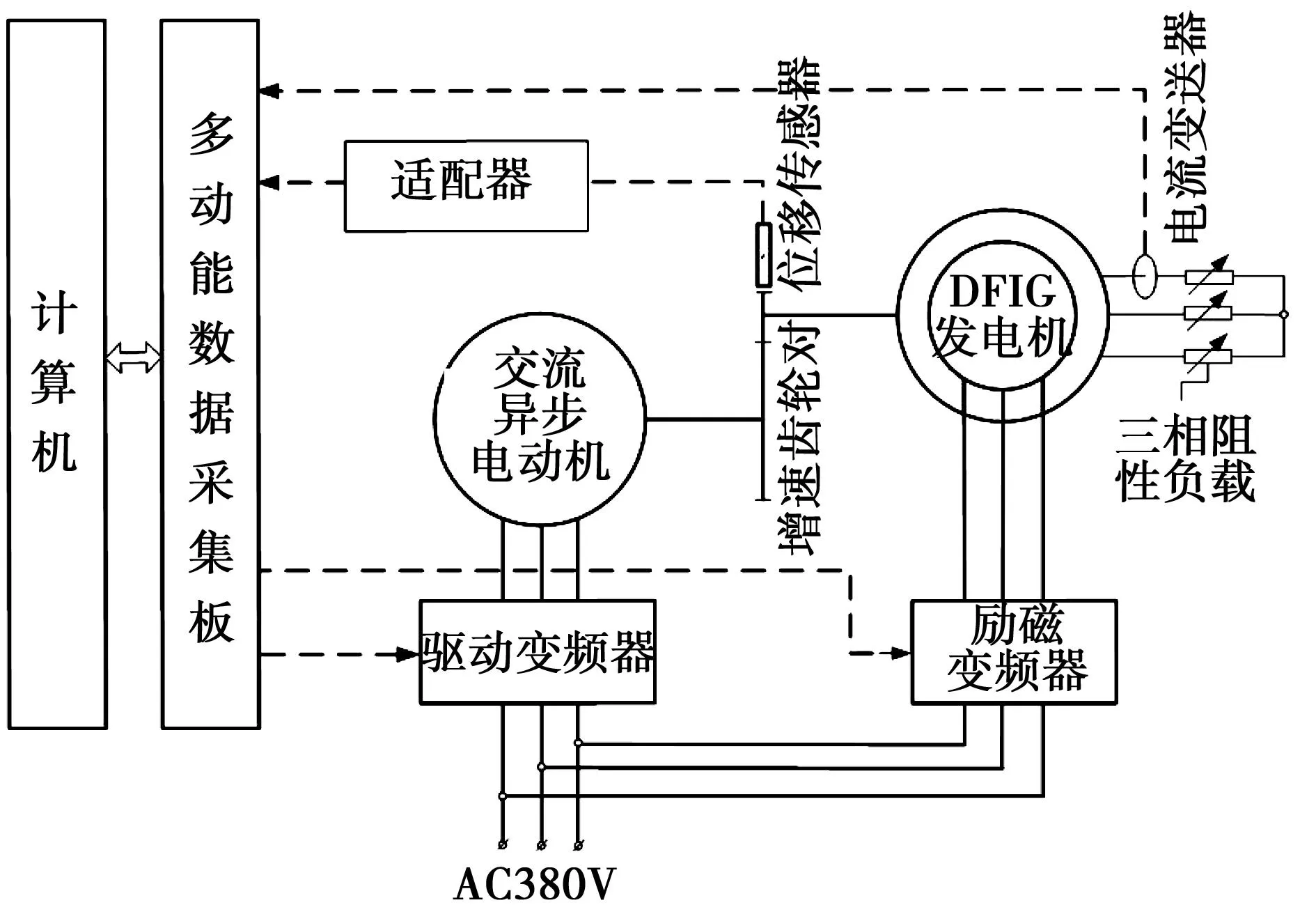
圖6　風電機組齒輪故障模擬實驗臺及　　　控制系統示意圖Fig.6　Diagram of wind turbine gear fault simulation　　　 test bench and the control system

圖7　風電機組齒輪故障模擬實驗臺照片Fig.7　Photo of the wind turbine gear fault　　　 simulation test bench

5Hilbert變換幅值和頻率解調原理

設x(t)為一個實時域信號，其Hilbert變換定義為

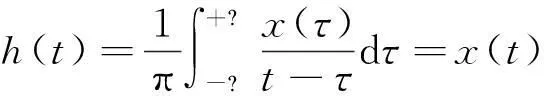
(11)

則原始信號x(t)和它的Hilbert變換信號h(t)可以構成一個新的解析信號

z(t)=x(t)+jh(t)=a(t)ejφt。

(12)

其幅值

(13)

等于為原始信號x(t)的幅值解調信號，對其進行FFT分析即得幅值解調譜或稱包絡譜。

(14)

為相位解調信號。相位解調信號的導數即為瞬時頻率，即瞬時頻率解調信號

(15)

或

(16)

對其進行FFT分析即得瞬時頻率解調譜。

6齒輪故障模擬仿真結果分析

仿真時，在齒輪故障模擬仿真子模塊的fz輸入端接一個方波信號，模擬k(t)的理想變化規律，方波頻率為齒輪的嚙合頻率fz；另一個輸入端接一個簡諧信號或常數，其中為簡諧信號時模擬齒輪有局部故障；為常數時模擬正常齒輪。

當圖5中的手動開關K1切向常數1時，相當于齒輪的動力學方程(8)中的E2(t)為恒定值，即系統激勵只與k(t)有關，系統為正常狀態，無故障。仿真時，轉子平均轉速為ωr2=47.124 rad/s，轉子供電頻率f2=35 Hz，此時的發電頻率為

f1=pnfr2+f2=

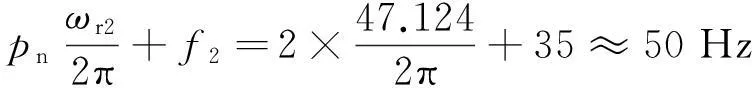
利用式(13)和式(16)計算出的幅值譜、幅值包絡譜和瞬時頻率解調譜如圖8所示。可見定子電流信號除50 Hz的工頻分量外，沒有其它明顯的頻率成分。

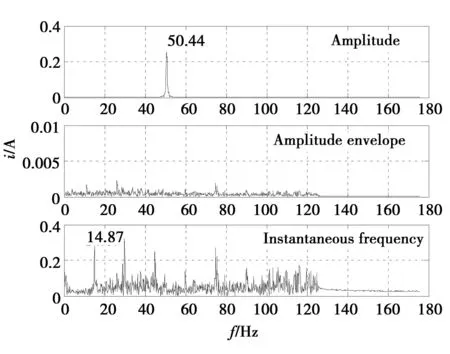
圖8　正常時發電機定子電流頻譜　　　(f2=35 Hz,ωr2=47.124 rad/s)Fig.8　Spectrum of generator stator current in normal　　　times(f2=35 Hz,ωr2=47.124 rad/s)

當圖5中的手動開關K1切為簡諧信號輸入時，可以模擬齒輪有局部故障。若模擬大齒輪故障，只需設定故障頻率為該軸轉頻，如fr1=3 Hz，此時的定子電流頻譜如圖9所示。與圖8相比，在幅值譜中明顯可以分辨出由于轉矩和速度波動引起的發電主頻率(50 Hz)上調制有邊帶成分，雖然沒有在幅值包絡譜上發現調制成分，但是在瞬時頻率譜中可以清楚地得到轉速波動的2.89 Hz成分，說明在離網狀態下，發電機的發電頻率波動主要是由斷齒故障引起的速度波動導致的，其波動頻率與模擬故障頻率一致。

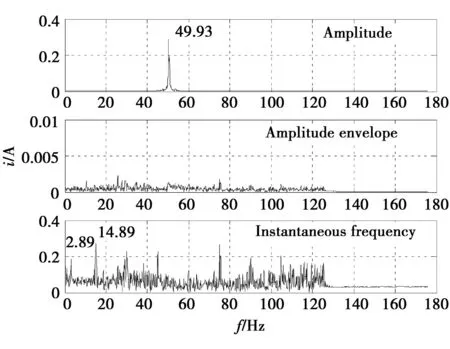
圖9　模擬故障時發電機電機定子電流頻譜　　　(f2=35 Hz,ωr2=47.124 rad/s,fr1=3 Hz)Fig.9　Spectrum of generator stator current when　　　 simulate fault(f2=35 Hz,ωr2=47.124 rad/s,　　　fr1=3 Hz)

7齒輪模擬故障時的實驗臺驗證

在圖6所示的試驗臺上進行了模擬實驗驗證。試驗時，發電機轉子供電電壓為100 V，頻率35 Hz；電動機定子供電頻率10 Hz，測得發電機定子側的相電流信號的頻譜如圖10所示。 可以在看出對應的大小齒輪軸的轉頻2.91 Hz和4.61 Hz，其中4.61 Hz是發電機軸的轉頻。由于發電機的安裝問題，其多少存在一定的不平衡或不對中現象，所以會出現這個頻率成分。2.91 Hz為模擬風輪軸的轉頻，正常齒輪時，在發電機定子電流中不應該出現此頻率成分，實際該軸上的大齒輪有1個模擬斷齒，導致每轉產生一次沖擊，所以該軸的旋轉頻率(約2.91 Hz)就反映在發電機定子電流信號中。

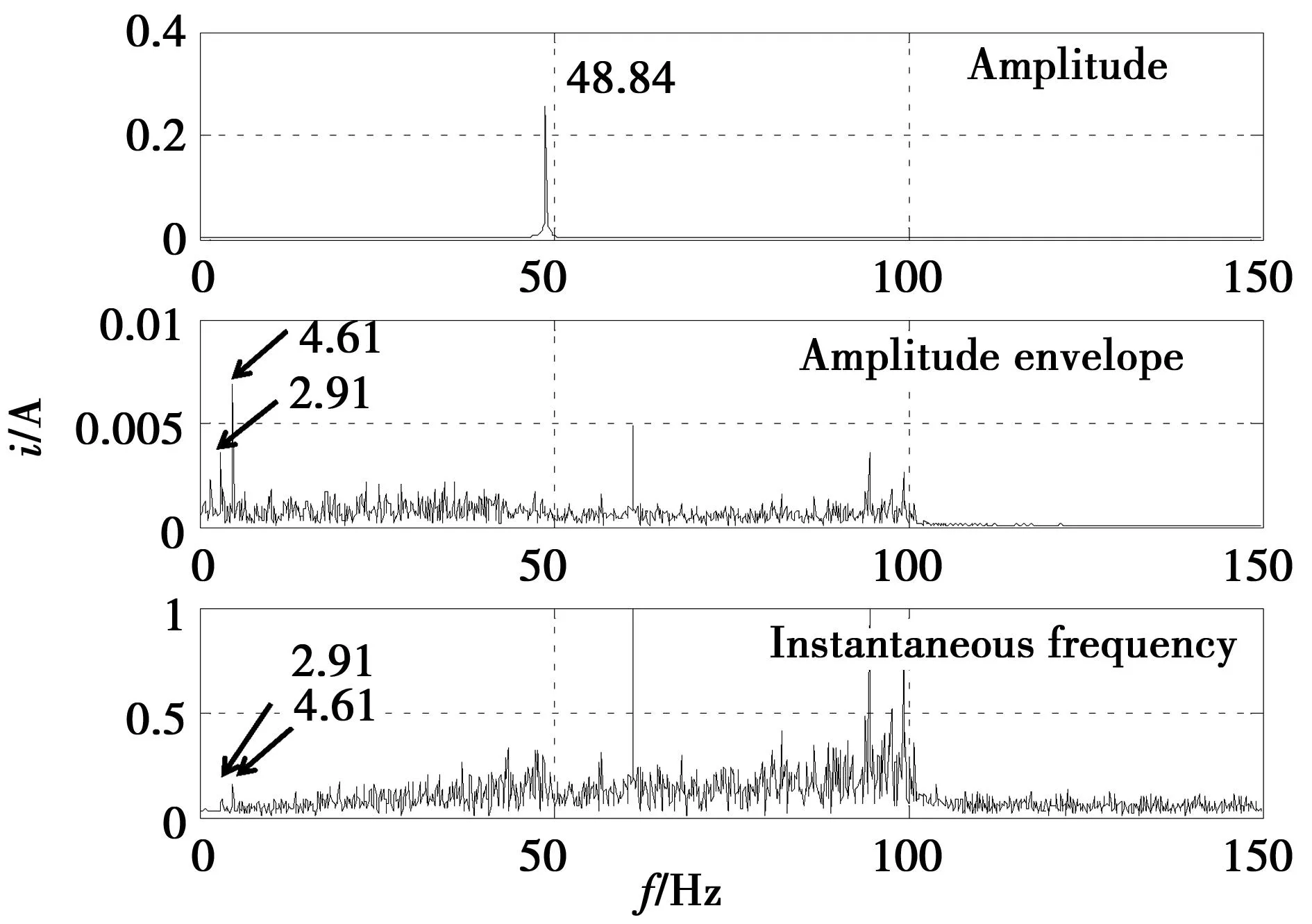
圖10　模擬斷齒故障時發電機定子電流頻譜　　　(f2=35 Hz，電動機定子供電頻率10 Hz)Fig.10　Generator stator current signal spectrum when　　　simulate broken teeth fault(f2=35 Hz,power　　　frequency of motor is 10 Hz)

8結論

通過對理論仿真和試驗結果的對比分析，說明本文提出的機電聯合仿真模型是可行的，表明發電機電流信號能夠準確反映機械故障的特征信息。另外，在離網環境下，理論仿真表明，機械故障信息主要以頻率調制的形式出現，意味著發電機發電頻率發生了波動現象。而幅值調制現象較弱，但是，從試驗臺模擬測試結果可以看出，實際上幅值調制和頻率調制均是存在的，這說明仿真模型只能考慮單一的條件，而實際情況下，由于實驗設備本身的各種故障及安裝誤差的影響，電流信號并不是模擬的理想狀態，這一點通過振動等分析可以驗證。

參 考 文 獻:

[1]沈艷霞，李帆. 風力發電系統故障診斷方法綜述[J]. 控制工程, 2013,20(3):789-793.

SHEN Yanxia, LI Fan.A survey of diagnosis methods for wind power system[J]. Control Engineering of China,2013, 20(3),789-793.

[2]陳雪峰,李繼猛, 程航, 等. 風力發電機狀態監測和故障診斷技術的研究與進展[J].機械工程學報, 2011,47(9):45-52.

CHEN Xuefeng, LI Jimeng, CHENG Hang, et al. Reseasch and application of condition monitoring and fault diagnosis technology in wind turbines[J]. Journal of Mechanical Engineering, 2011, 47(9):45-52.

[3]ROYO J,ARCEGA F J.Machine currentsignature analysis as a way for fault detection in squirrel cage wind generators [C]//2007 IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, SDEMPED, 2007:383-387.

[4]馬宏忠, 張志艷,張志新, 等. 雙饋異步發電機定子匝間短路故障診斷研究[J]. 電機與控制學報, 2011,15(11):45-52.

MA Hongzhong, ZHANG Zhiyan, ZHANG Zhixin, et al. Research on DFIG stator winding inter-turn short circuit fault[J]. Electric Machines and Control, 2011,15(11):45-52.

[5]YANG Wenxian,TAVNER P J,CRABTREE C J,et al.Cost-effective condition monitoring for wind turbines [J]. IEEE Transaction on Industrial Electronics, 2010, 57(1): 263-271.

[6]AMIRAT Y,CHOQUEUSE V,BENBOUZID M E H. Wind turbines condition monitoring and fault diagnosis using generator current amplitude demodulation[C]//2010 IEEE International Energy Conference and Exhibition, 2010: 310-315.

[7]AMIRAT Y,CHOQUEUSE V,BENBOUZID M E H,et al.Bearing fault detection in DFIG-based wind turbines using the first intrinsic mode function[C]//19th International Conference on Electrical Machines, ICEM 2010, 2010:1-6.

[8]周真,周浩,馬德仲, 等. 風電機組故障診斷中不確定性信息處理的貝葉斯網絡方法[J].哈爾濱理工大學學報, 2014,19(1): 64-68.

ZHOU Zhen, ZHOU Hao, MA Dezhong, et al. Method of Bayesian network for uncertainty information processing of wind turbines fault diagnosis[J].Journal of Harbin University of Science and Technology, 2014,19(1): 64-68.

[9]熊飛,王雪帆, 華斌，等. 繞線轉子無刷雙饋電機的d-q軸數學模型[J]. 電機與控制學報, 2015,19(5):81-89.

XIONG Fei,WANG Xuefan,HUA Bin, et al.D-q axis mathematical model of wound-rotor brushless doubly-fed machine[J]. Electric Machines and Control, 2015, 19(5):81-89.

[10]楊建國, 姜立標, 林波,等. 變速器齒裂及軸承故障建模與故障特征提取[J]. 汽車工程, 2004, 26(2):224-228.

YANG Jianguo, JIANG Libiao, LIN Bo, et al. Modeling and feature extraction for tooth crack and bearing faults in transmission[J]. Automotive Engineering,2004, 26(2):224-228.

[11]師楠，朱顯輝.風電并網的頻率控制問題[J].哈爾濱理工大學學報，2012,17(2)：84-88.

SHI Nan, ZHU Xianhui. The frequency control issues about wind farm grid integration[J].Journal of Harbin University of Science and Technology, 2012, 17(2):84-88.

(編輯：張楠)

Research of electromechanical simulation model of wind turbine drive train fault diagnosis

SHI Xian-jiang,FANG Qin-guo,ZHAO Xiao-wen,DU Heng,SI Jun-shan

(School of Mechanical and Power Engineering, Harbin University of Science and Technology, Harbin 150080, China)

Abstract:In order to study the response process of the wind turbine drive train gear fault in the generator current signal,the application range of the current signal diagnostic methods was extended.On the basis of considering the gear mesh stiffness change and simulating the broken gear fault characteristics,the gear dynamics model was built.Taking a typical doubly-fed wind power generator as object,models of doubly-fed generator were set up and its control system using gears and speed parameters of generator was used to link the two models,and electrical and mechanical joint simulation model were constructed.Current fault feature was simulated in the situation of broken teeth gear and normal gear in theory,and the results were compared with the simulation fault test in test-bed. Simulation and experimental results show that the generator stator current accurately reflects the characteristics of the gear fault information, and it mainly causes frequency modulation of current signal in the condition of off-grid.

Keywords:wind turbine generation; drive train; gear; stator current; fault diagnosis; simulation

收稿日期:2014-12-16

基金項目：國家自然科學基金(51275136)

作者簡介：時獻江(1962—)，男，博士，教授，研究方向為機械故障診斷；

通信作者:時獻江

DOI:10.15938/j.emc.2016.07.011

中圖分類號:TM 315

文獻標志碼:A

文章編號:1007-449X(2016)07-0082-06

房欽國(1990—)，男，碩士研究生，研究方向為機械故障診斷；

趙曉文(1989—)，男，碩士研究生，研究方向為機電系統自動化；

杜恒(1989—)，男，碩士研究生，研究方向為機械故障診斷；

司俊山(1962—)，男，碩士，教授，研究方向為機電一體化。