向量教學要有結構性與邏輯性

王娜

[摘 要] 在平面向量等內容的教學當中，概念多且層次感不是很強，學生掌握得也不是很好. 同時學生對向量的認識折射出高一的教學存在很大的問題：學生的機械記憶來源于我們對向量概念教學的不到位，沒能使學生真正理解，因此導致學生對向量的認識只停留在套用公式的淺層認識上. 其原因是在講概念的過程當中，只注重了概念本身的描述，忽視了概念之間的結構性與邏輯性. 這說明向量教學要有結構性和邏輯性.

[關鍵詞] 平面向量；物理背景；實數類比

[?] 問題提出

在平面向量等內容的教學當中，概念多且層次感不是很強，學生掌握得也不是很好. 如2008年王寬明在《高中學生運用平面向量解決問題的影響因素分析》和2011年陸燕的《新課改下高中向量的教學研究》通過調查得出，學生對向量的認識折射出高一的教學存在很大的問題：學生的機械記憶來源于我們對向量概念教學的不到位，沒能使學生真正理解，因此導致學生對向量的認識只停留在套用公式的淺層認識上. 在筆者的教學當中也發現了同樣的問題. 分析其原因是在講概念的過程當中，只注重了概念本身的描述，忽視了概念之間的結構性與邏輯性. 由此，向量教學要有結構性和邏輯性.

平面向量的特征

《課標》指出：向量是近代數學中重要和基本的數學概念之一，它是溝通代數、幾何與三角函數的一種工具，有著極其豐富的實際背景. 在本模塊中，學生將了解向量豐富的實際背景，理解平面向量及其運算的意義，能用向量語言和方法表述與解決數學和物理中的一些問題，發展運算能力和解決實際問題的能力.

1. 平面向量的起源——豐富的物理背景

英國數學家哈代曾說：“還沒有哪個數學家純到對物理世界毫無興趣的地步”，所以說，數學和物理學的關系在中學階段應該得到重視和發展，事實上一個良好的物理學習是學生對數學產生興趣和學好數學的重要因素，尤其到今天，數學和物理學的關系是有目共睹的. 而向量在力學中的應用即使在中學階段也是不難發現的. 使學生盡早地認識到數學與物理世界的緊密關系，不僅可以增強學生學習的興趣，同時也使學生認識到數學偉大的社會性.

2. 向量的運算——代數學的基本研究對象

向量可以進行加、減、數乘、數量積（點乘）、向量積（叉乘）等多種運算，這些運算及其規律賦予向量集合特定的結構，使得向量具有一系列豐富的性質. 向量的運算及其性質自然成為代數學的研究對象.

3. 平面向量的應用——代數幾何的完美結合

向量是一個具有幾何和代數雙重身份的概念，同時向量代數所依附的線性代數是高等數學中一個完整的體系，具有良好的分析方法和完整結構，通過向量的運用對傳統問題的分析，可以幫助學生更好地建立代數與幾何的聯系，也為中學數學向高等數學過渡奠定了一個直觀的基礎. 這方面的案例包括平面幾何、立體幾何和向量解析幾何.

平面向量教學的結構性與邏輯性

針對向量的三個特征，要有結構性和邏輯性地安排平面向量章節的教學.

1. 以物理背景為主線教學

向量的每一個定義都有其物理背景，所以以物理背景為主線進行教學，可以讓知識之間更具備結構性.

如，以力、位移等矢量為背景引入向量的定義，以位移為例講解有向線段的三要素，以位移的合成為背景講解向量的加減法的三角形法則，以力的合成為背景講解平行四邊形法則，以輪船過河為背景深化向量的加減法法則.

如，以自由落體的速度公式vt=gt體會向量數乘運算的存在，也可以位移的倍數或者速度的倍數為背景體會位移的倍數依然是位移，速度的倍數依然是速度. 這樣可以使學生對向量的數乘運算的結果仍然是一個向量有直觀的認識.

在引入向量的數量積運算時，可以力做的功為背景. 一個物體受到力F的作用，如果在力的作用方向上發生一段位移s，我們就說這個力對物體做了功.如果力F的方向與位移s的方向相同，功的大小就等于力的大小F與位移s大小的乘積，即Fs. 如果力F的方向與位移s的方向成θ角，那么與位移s方向相同的分力為F1=Fcosθ，物體在力F1的方向上產生了位移s，因而對物體做的功為F·scosθ. 總之，力所做的功是一個標量，它是由兩個向量——力和位移所決定的，這正是向量的數量積的意義. 在引入向量的一些運算律時，也可以力做功為背景.當力擴大幾倍時，力所做的功也相應擴大幾倍，得出向量的數乘運算與數量積運算滿足結合律：（λa）·b=λ（a·b）；兩個力的合力所做的功等于這兩個力分別所做的功的和，向量的加法運算滿足分配律：（a+b）·c=a·c+b·c. 具體如表1：

2. 與代數學中研究數集的類比進行教學

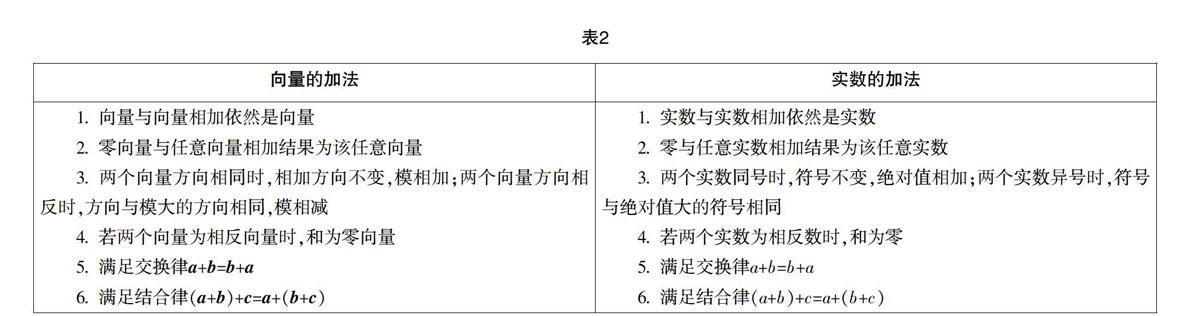
在研究數集的過程中，0和1是最特殊的數，要進行特殊的研究，如0與任何實數a相加都等于a，0與任何實數相乘都等于0，1與任何實數相乘都等于這個實數. 同理，整數之間進行的加、減、乘的運算是封閉的，也就是運算之后依然是整數，但整數之間除的運算是有理數集. 把數集研究的這些方法和性質，類比到向量的教學，可以使向量的每一個定義都順理成章，并且具備內在的邏輯性，不至于顯得那么零散. 在講解向量定義之后，自然就要研究特殊的向量，零向量和單位向量，繼而研究向量之間的加法和減法以及數乘和其運算定律. 可以發現這兩個不同的代數結構在本質上是相同的，即有類似的運算和運算法則. 不同的只是兩個代數結構的元素有所區別. 可見從進一步抽象的角度來看，無論是向量代數系統還是我們熟悉的實數代數系統都是某一個更一般或更抽象的數學模式——歐幾里得空間在一定情況下的特例而已. 如表2：

3. 從幾何方面理解向量

向量的知識點之間也是有內在的邏輯聯系的，找到各知識點之間的聯系，可以強化知識體系，讓學生更好地理解向量的本質.

向量是具有大小和方向的量，于是向量只有平移和旋轉的兩種變化方式.根據向量有自由向量的特征，使得向量在平移的過程當中是不變的. 于是在平移的基礎上，得到了向量加減法的三角形法則和平行四邊形法則. 在平移的過程中若模發生變化，則產生向量數乘的定義. 在學習了數乘和向量的加減法之后，將其結合在一起就引入了平面向量基本定理. 在確定了兩個基底之后，將線性運算與坐標進行了結合，得到了平面向量的坐標表示. 以上都是平移的應用，但是向量之間的旋轉呢？這就引入了平面向量的數量積，完成向量由平移到伸長到旋轉的過程.

從幾何的角度來說，幾何解決的就是平行，旋轉以及旋轉中特殊的垂直問題. 向量是研究幾何的有效工具，我們可以利用向量的數乘及向量的加減法來研究幾何問題. 但是會出現向量個數太多的問題，平面向量基本定理解決了這個問題. 在眾多基底當中，發現兩個互相垂直的單位向量為基底更具備優勢，引入了向量的坐標運算，這與實數和坐標軸的關系一樣. 引入了向量的數量積則解決了所成角的問題.

綜上，在向量的教學當中注重知識的結構性和邏輯性可以讓學生從本質上理解知識之間的聯系，同樣的教學方式也可以應用到集合等概念的教學當中，從而形成良好的知識體系. 讓學生將知識點縱向穿成線，再橫向連成網，學習中只要觸碰到一個知識點就會引起對橫縱向知識點的思考，對于學生思維的培養和數學的應用起到不可估量的作用.