漫談什么是解題

王惠

?

漫談什么是解題

王惠

簡單地說，解題就是求出未知結論的過程。羅增儒先生說：“解題就是解決問題，即求出數學題的答案。這個答案在數學上也叫做解。所以，解題就是找出題的解的活動。小至一個學生算出作業的答案，一個教師講完概念的構建與定理的證明，大至一個數學課題得出肯定或否定的結論，一個數學技術應用于實際、構建出適當的模型等，都叫做解題。”

波利亞發現，在日常解題和攻克難題而獲得數學上的重大發現之間并沒有不可逾越的鴻溝。他說：“一個重大的發現可以解決一些重大的問題，但在求解任何問題的過程中，都會有點滴的發現。”“一個有意義的題目的求解，為解此題所花的努力和由此得到的見解，可以打開通向一門新的科學的大門。”

大家非常熟悉的哥尼斯堡七橋問題，歐拉解決了，也就是說，歐拉解答了這個問題，由此創立了圖論這個數學分支，即誕生了新的科學。像這樣的例子，在數學上不勝枚舉。這就驗證了波利亞上面的論述。

波利亞主張把解題作為培養學生的數學才能和教會他們思考的一種手段與途徑。這一主張得到了國際數學教育界的贊同。1976年，國際數學管理者委員會把解題能力列為十項基本技能的首位，美國數學教師聯合會理事會把解題提到了“1980年代學校數學教學的核心”之高度。可見，解題對數學學習的重要。

例1“！”表示階乘運算，如2！=2×1，3！=3×2× 1，求！的值。

分析：將各階乘數轉化為乘法運算，并找出消掉一些數的方法。不然的話，直接計算會相當繁雜，也不是此題的本意。這就聯想到階乘運算中的公式：n· n！=（n+1）！-n！。通過觀察可知，公式左邊有點像題目的左邊，右邊出現了減法，那就有可能消掉某些數。沿著這個思路試試，也許會有驚喜。

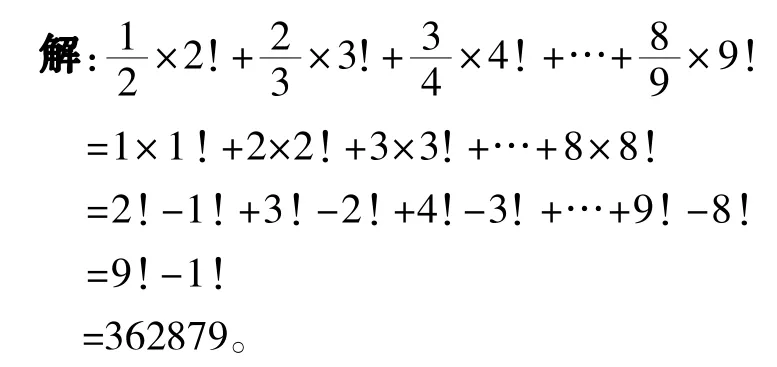
例2n是自然數，n2+n+11是素數嗎？

分析：目前還沒有表示所有素數的公式，那么，可以肯定所表示的數不可能全是素數。這就需要找出n2+n+11能表示哪些素數。解題方向明確了，我們就可以開始尋找解題方法。顯然，n2+n+11在實數范圍內不能分解因式，我們只能采取取值辦法一一驗證，找到結論。

解：記（fn）=n2+n+11，則分別令n=1，2，3，4，5，6，（fn）的值為13，17，23，31，41，53。顯然這些數都是素數。是不是（fn）表示的所有的數都是素數？還需要繼續驗證。

令n=7，8，9，（fn）分別為67，83，101。還要驗證嗎？要！

令n=10，（fn）=121=112，不是素數！

因此，n2+n+11所表示的數不全是素數。

例350條直線最多能將平面分成多少部分？

分析：50條直線，多了點吧？畫出50條直線來找答案，估計難以找到一個會這樣解的人！怎么辦？先畫幾條直線，從中找找分平面數的規律。

解：分別作出1條～5條直線分平面的情況，見下圖。

它們分平面的部分數分別為2，4，7，11，16。再將這5個數分解為2=1+1，4=1+1+2，7=1+1+2+3，11= 1+1+2+3+4，16=1+1+2+3+4+5。

這樣，規律就凸顯出來了。

我們從這3道題的解答過程中可以看到數學思維方法的運用。如靈活運用（n+1）！-n！=n·n！，將復雜的運算式子變得簡便；要否定一個命題，只要舉出一個反例即可；從最簡單的情形出發，遞推出結論。

解題過程中，很重要的一步就是要充分挖掘已知條件，顯性的、隱性的都要充分利用。如例1中，等式（n+1）！-n！=n·n！是不可能告訴你的，必須根據階乘的運算挖掘出來。如果沒有這個等式的運用，計算量將會大大增加。事實上，由條件挖掘隱性的東西是成功解題的關鍵。

（作者單位：安鄉縣圍庵小學）