基于人工魚群算法的位移型阻尼器位置和參數的優化方法
閆維明, 杲曉龍, 謝志強, 彭凌云
(北京工業大學 建筑工程學院,北京 100124)
基于人工魚群算法的位移型阻尼器位置和參數的優化方法
閆維明, 杲曉龍, 謝志強, 彭凌云
(北京工業大學 建筑工程學院,北京100124)
摘要:對耗能減震結構中,阻尼器參數和位置決定著結構的減震效果。基于人工魚群算法提出一種針對位移型阻尼器優化設計的人工魚群優化模型,模型面向以有限元模型表示的多維多自由度實際結構,對各層位移型阻尼器的位置和參數進行優化。針對結構中添加位移型阻尼器會使結構層剪力增大的問題,提出一種同時考慮結構各樓層層間位移角、各樓層加速度和層剪力變化的優化目標函數,同時利用均方根的形式更加有效的反應各響應在地震波峰值段的變化特性。結構減震控制優化設計時可根據結構的不同設計需求修正目標函數的加權系數。最后,通過數值算例驗證本文優化模型的有效性。
關鍵詞:耗能結構;位移型阻尼器;魚群算法;阻尼器位置;阻尼器參數
結構減震控制是指在結構的特定部位添加耗能裝置來減小結構的振動反應,以滿足結構抗震安全性的要求。耗能減震結構中采用的阻尼器分為位移型阻尼器和速度型阻尼器。其中位移型阻尼器的性能主要由屈服力和初始剛度兩個參數確定。采用位移型阻尼器對結構進行減震控制時阻尼器參數、位置、數量決定著阻尼器的減震效果,因此對阻尼器的參數、位置和個數進行優化計算有著重要意義,而優化算法、結構模型以及目標函數的選擇對耗能減震體系的優化結果有著至關重要的影響。
國內外學者在阻尼器的參數和位置優化方面進行了深入研究,并提出不同的優化模型。Takewaki[1]基于結構傳遞函數,通過最小化結構層間位移角得到阻尼器的最優控制參數。Aydin等[2]通過建立與耗能器參數相關的拉格朗日方程,利用順序搜索法求解耗能器參數的最優解。Mousavi等[3]通過建立與層間位移角相關的頻域方程,利用逐步增量法得到阻尼器參數的最優解,并提出實際建筑結構的設計流程。Singh等[4-6]利用遺傳算法求解阻尼器的最優參數。Singh等[7-10]利用遺傳算法對阻尼器的位置進行優化。
以往的優化算法中[4-9],多數研究者將結構各層簡化為兩個平動或兩個平動加一個轉動的單質點體系,而實際結構是多維多自由度體系,模型的過度簡化導致傳統優化結果僅能給結構減震控制提供參考,無法直接應用于實際工程。同時已有關于位移型阻尼器的優化算法大多是對阻尼器參數和位置分別進行優化計算[9],但阻尼器的參數、位置和個數之間存在密切關系,以往的串行優化模式極有可能丟失系統的最優解。近年來,智能算法快速發展并成為解決多目標優化問題的有效手段。在這些智能算法中,人工魚群算法具有并行性、簡單性、快速性等特點,因此在多目標優化方面得到了廣泛關注和應用。周麗萍等[11]利用魚群算法對鋼結構-控制系統進行協同優化設計。李亮等[12]利用魚群算法求解兩個復雜土坡的最小安全系數。已有成果表明利用魚群算法求解結構減震控制中的多目標優化問題具有可行性和優越性。此外,當采用位移型阻尼器對結構進行減震控制時,會出現結構構件內力增加的情況[13],構件內力的增加是由于結構層剪力的增大而引起的,而已有的阻尼器優化目標函數較少考慮層剪力的變化,很可能影響實際的減震效果。
針對上述研究中存在的問題,本文建立了一種面向實際減震結構的位移型阻尼器優化模型。提出考慮層剪力變化的優化目標函數,目標函數中引入均方根的概念,更加有效的反應結構各響應在地震波峰值段的變化特性。通過構建優化算法與有限元軟件的接口,使優化算法能夠直接指導結構有限元模型的建立和調整。在優化過程中,通過限定阻尼器在多遇地震時提供給結構的附加阻尼比對位移型阻尼的參數和位置進行同步優化。此外,通過偽并行計算思想的引入,即在每次迭代計算時首先進行各層尋優,然后再整合各層優化結果進行整體分析最終得到最優解。
1阻尼器參數和位置優化的數學模型
1.1優化目標函數的建立
結構各層加速度、層間位移角和層剪力都是影響結構安全性和舒適度的重要指標,阻尼器的參數和位置優化的目的就是在阻尼器個數一定的條件下,求解阻尼器的最優參數和最優布置位置,使得上述控制指標對應的數值盡量小。介于目標函數中單一的控制指標可能會造成其他控制指標的增大[9],同時為了更加有效的反應各指標在地震波峰值段的響應大小,本文目標函數采用有控結構在地震作用下,時程分析得到的各層加速度、層間位移角和層剪力在地震波峰值段的均方根數值的最大值與其相應的無控結構對應的各響應的均方根的最大值比值的無量綱線性組合。通過改變加權系數的大小決定對各個指標的優化控制程度,定義目標函數如下:
Z=sum(σdi)
(1)
式中:
(2)
式中,wA、wB、wC分別代表各項的加權系數,σAi,max、σBi,max、σCi,max分別代表有控結構第i層的層間位移角、絕對加速度和層剪力在峰值段均方根的最大值。σA0i,max、σB0i,max、σC0i,max分別代表無控結構第i層的層間位移角、絕對加速度和層剪力在峰值段均方根的最大值。均方根的表達式為:
(3)
式中,n為地震波峰值段的步數,xi為地震波作用下各響應。
1.2優化參數關系的確定
為了使位移型阻尼器在設防和罕遇地震下更加有效地保護主體結構,阻尼器在設防地震作用下提供給結構的附加有效阻尼比應大于多遇地震作用下的附加有效阻尼比[14]。本文優化模型中通過限制多遇地震作用下位移型阻尼器提供給結構的附加阻尼比來滿足上述要求。同時為了減少優化變量,推導了附加有效阻尼比、阻尼器的參數和位置之間的關系,推導過程如下:
位移型阻尼器一般通過與連接件的串聯布置在結構的層間位置,假定位移型阻尼器的本構關系為圖1所示的理想彈塑性模型,包括2個參數:彈性剛度Kd、屈服強度fy。

圖1 位移型阻尼器滯回模型Fig.1 Hysteretic model of the displacement-based energy dissipative devices
《建筑抗震設計規范》(GB 50011-2010)[15]規定,消能部件附加有效阻尼比可按下式估算:
(4)
式中,ζa為消能減震結構的附加有效阻尼比;Wcj為第j個消能部件在結構預期層間位移下往復一周所消耗的能量;Ws為設置消能部件的結構在預期位移下的總應變能。
不計及扭轉影響時,消能減震結構在水平地震作用下的總應變能,可按下式估算:
Ws=(1/2)∑Fiui
(5)
式中:Fi為質點i的水平地震作用標準值;ui為質點i對應于水平地震作用標準值的位移。
圖1所示的單個位移型阻尼器滯回耗能計算公式如下:
Wcj=4KdDd(d-Dd)=4fy(d-Dd)
(6)
式中,Kd為阻尼器的初始剛度;Dd阻尼器的屈服位移;d為阻尼器兩端的位移。fy為阻尼器的屈服力。
假定整個結構總共添加nf個阻尼器,所有阻尼器的耗能相等。由式(3)可得單個阻尼器的耗能可表示為:
Wcj=4πWsξa/nf
(7)
根據式(5)~式(6)可求得各阻尼器的初始剛度與阻尼器屈服力、消能減震結構總應變能、阻尼器的兩端位移、消能部件附加給結構的有效阻尼比之間的關系如下:
(8)
模型在優化計算時,阻尼器的位置確定后可確定阻尼器兩端的位移d,優化計算時可根據阻尼器的個數nf和屈服力fy和結構的應變能Ws確定阻尼的初始剛度。
1.3約束條件
(1)
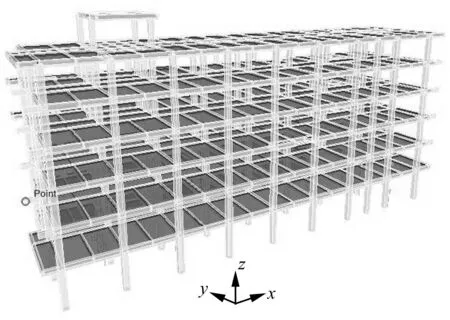
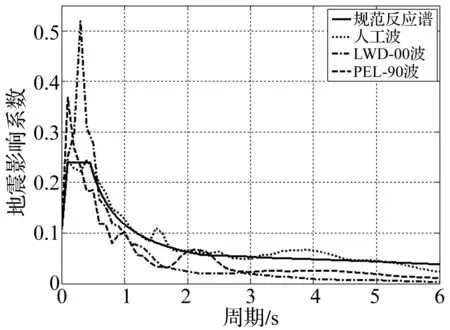
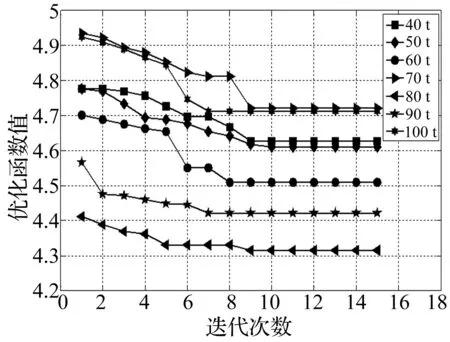
0 (9) 0 (10) 式中,f、k分別指由阻尼器性能決定的阻尼器的噸位和初始剛度。 (2) θimax-θ≥0 (11) 式中,θimax和θ分別指結構的各層層間位移角最大值和規范規定的層間位移角限制。 (3) ξa-ξ0=0 (12) 式中,ξa指阻尼器附加給結構的有效阻尼比,ξ0指為保證位移型阻尼器在設防和罕遇地震下更加有效地保護主體結構而設定的阻尼器在多遇地震作用下提供給結構的附加阻尼比。 (4) 阻尼器的布置位置需要滿足建筑要求,阻尼的個數可根據工程預算初步確定。 2阻尼器參數和位置的優化 2.1人工魚群算法的優化原理 人工魚群算法[16]是集群智能思想的一個具體應用,它不需要了解問題的特殊信息,只需要對問題進行優劣比較,算法主要通過單條人工魚的覓食、聚群和追尾三個個體行為來尋求全局最優值。算法具有并行性、簡單性、全局性、快速性、跟蹤性等特點。算法中隨機因素少,基本上可以步步向最優搜索。本文在基本人工魚群算法的基礎上開發偽并行魚群算法優化模型,將其用于位移型阻尼器的參數和位置的優化。 人工魚狀態{X}=(x1,j,k,x2,j,k,…,xi,j,k,E),其中xi,j,k表示阻尼器的空間位置,i表示第i條人工魚,j表示第j個樓層,k表示第k個阻尼器,{E}為阻尼器的參數向量。di,j=‖Xi-Xj‖表示人工魚個體之間的歐式距離。本文距離可以表示為:假定兩個決策變量A={a1,a2,…,an}和B={b1,b2,…,bn},A和B分別代表兩條魚中的某一樓層阻尼器的位置。則它們之間的距離可表示為: (13) (14) 人工魚的覓食行為是魚類的本能行為之一,表現為魚在視野范圍內的探尋活動,該行為保證人工魚向最優狀態持續行進。本文人工魚在覓食行為中通過尋求各層層間位移角最大值對應的豎向構件,在距離最大層間位移角對應的豎向構件最近的位置添加阻尼器來指導人工魚的游動方向,并通過給定次數的迭代計算使得人工魚向著最優方向行進。人工魚追尾行為,是一種向鄰近的有著最高適應度的人工魚追逐的行為,在算法中可以理解為是向附近的最優伙伴靠近的過程。假定人工魚當前狀態Xi,探索當前領域內(di,j 2.2人工魚群算法的優化過程 基于上述基本人工魚群算法的原理、優化參數及優化目標,在多遇地震作用下對添加位移型阻尼器的結構進行優化時,為了使位移型阻尼器在設防和罕遇地震下更加有效地保護主體結構,要求阻尼器在多遇地震作用下提供給結構的附加阻尼比不宜太大,建議取值1%。根據確定的附加阻尼比、阻尼器個數和噸位即可按照下述流程進行計算。 1) 首先初始化生成NP條人工魚,初始化公告牌。根據建筑要求、結構特性和阻尼器個數在對應樓層,可添加阻尼器的位置隨機布置阻尼器。 2) 假定各個阻尼器耗散相同的能量且每個樓層X、Y向布置相同參數的阻尼器。給定一個阻尼器的屈服力后可根據式(7)在給定附加有效阻尼比的情況下確定各層阻尼器的初始剛度,此時結構中的阻尼器單元被賦予屬性,使得式(7)中的結構應變能發生變化,因此需要迭代計算調整阻尼器的初始剛度,直到多遇地震作用下阻尼器提供給結構的附加有效阻尼比滿足約束條件(3)。 3) 啟動迭代優化,各條人工魚分別執行覓食、聚群和追尾行為,將其得到的優化結果與公告牌進行對比并及時更新公告牌。 4) 對不同噸位阻尼器下對應的優化結果進行對比分析,在優化結果中選擇合理的阻尼器參數和布置方式。 5) 用規范規定的其他地震波對優化結果進行回歸驗證,判斷得到的阻尼器優化布置方案在其它地震波作用下時能否使結構滿足規范要求。 綜上所述,位移型阻尼器參數和位置的優化過程如圖2所示。 圖2 算法流程圖Fig.2 Flow chart of algorithm 圖3 結構三維模型Fig.3 Structure model of three-dimensional 圖4 各條地震波對應反應譜與規范反應譜的比較Fig.4 The comparison between the response spectra of every seismic waves and standard response spectra 3算例 本文優化算法在MATLAB平臺上開發,建立了MATLAB與SAP2000有限元軟件的接口,結構計算在SAP2000中完成。 某鋼筋混凝土框架結構地下1層,地上6層,平面尺寸為57 m×16.3 m,結構總高度28.5 m。結構三維透視圖見圖3。按《建筑抗震設計規范》(GB50011-2010)要求抗震設防烈度為8度,設計基本地震加速度為0.30 g,設計地震分組為第二組,建筑場地類別二類,設計地震反應譜特征周期0.4 s。該結構主要問題是多遇地震作用下結構的層間位移角最大值X向為1/458,Y向為1/337,超過規范限值要求,擬通過在結構中布置位移型阻尼器使得結構滿足規范要求。根據結構特性、場地類別選取2條天然場地波和1條人工波對結構進行分析,地震波峰值加速度為110 gal。本文優化時選用對無控結構響應最大的人工波激勵結構,同時驗算罕遇地震作用下結構各響應的變化情況。各地震波影響系數曲線與規范反應譜的對比如圖4所示。 魚群算法中各參數選擇:人工魚的總個數為8,視野范圍為7,擁擠度因子為8,嘗試次數為10,總迭代次數為15,移動步長為4。每條人工魚代表一種阻尼器布置方案,本次優化時分別在結構的1~5層每層各布置8個位移型阻尼器。分別取屈服力40~100 t的阻尼器按照第2節所述優化過程對各位移型阻尼器進行位置和初始剛度的優化。 為了說明本文目標函數對結構層剪力控制的有效性,選用表1所示的兩種不同加權系數對應的目標函數對結構進行優化。目標1和目標2分別指目標函數中考慮和不考慮層剪力的變化。圖5~圖6給出了選擇不同噸位阻尼器時兩種目標函數下模型的迭代優化過程。 表1 加權系數 圖5 目標1對應迭代過程中目標函數的變化Fig.5 Transformation progress of function for the first goal 圖6 目標2對應迭代過程中目標函數的變化Fig.6 Transformation progress of function for second goal 從圖5和圖6可以看出目標函數中不考慮層剪力的變化時,阻尼器噸位的越大,對目標函數的優化結果越好,阻尼器噸位取100 t時得到的優化結果最佳。目標函數中考慮層剪力變化后, 80 t的阻尼器對應的優化結果最好。表2給出了兩種阻尼器布置方案對應的各層位移型阻尼器的初始剛度,可以看出,由于本文模型中限定了阻尼器提供給結構的附加有效阻尼比,因此噸位大的阻尼器對應的阻尼器的初始剛度偏大,間接表明本文目標函數對位移型阻尼器初始剛度的一個約束效果。 表2 阻尼器參數優化結果 按照上述得到的阻尼器的優化布置方案在結構中布置阻尼器,為了表明文中優化模型對阻尼器位置優化的有效性,在結構1~5層的四個邊角處每層布置8個阻尼器,阻尼器的參數選取表2中目標1對應的阻尼器參數。利用時程分析方法,計算各有控結構及無控結構各層層間位移角、加速度和層剪力在上述3條地震波作用下的峰值,根據計算結果繪制結構各響應峰值對比圖。限于篇幅,本文僅給出三條波作用下多遇地震和罕遇地震對應的結構層間位移角和層剪力的包絡曲線,如圖7~圖10所示。表3~表4給出多遇地震和罕遇地震作用下各有控結構各響應最大峰值和最大均方根值的減震效果對樓層的平均值。 圖7 多遇地震作用下層間位移角最大值優化對比Fig.7 The comparison of maximum story drift under frequent earthquake 圖7~圖8及表3可以看出:多遇地震作用下兩種控制方式均能使結構的層間位移角滿足規范要求,采用目標2對應的優化方案時,多數樓層的層間位移角峰值要小于目標1對應的層間位移角峰值,但目標2對應的層剪力峰值均大于目標1,甚至部分樓層層剪力大于原結構。在各樓層邊角處均勻布置阻尼器時,層間位移角響應較目標1和目標2對應的結果偏大,層剪力較目標1整體上略微偏大。圖9~圖10及表4可以看出:罕遇地震作用下,結構的層間位移角均能滿足規范要求,由于罕遇地震作用下結構中部分構件已進入非線性階段,減震效果相對多遇地震有所減小。目標2對應的結構層間位移角峰值最小,目標1對應的層間位移角峰值介于目標2和無優化之間,目標1對應的結構層剪力均小原結構,而目標2和無優化對應的部分樓層層剪力會出現增大的情況,表明本文提出的目標函數中考慮層剪力的必要性及本文優化模型的有效性。 表3 多遇地震作用下層間位移角和層剪力減震效果平均值比較 注:表中數據意義為“目標2(目標1)[無優化]”。 表4 罕遇地震作用下層間位移角和層剪力減震效果平均值比較 注:表中數據意義為“目標2(目標1)[無優化]”。 圖8 多遇地震作用下層剪力最大值優化對比Fig.8 The comparison of maximum story shear force under frequent earthquake 圖9 罕遇地震作用下層間位移角最大值優化對比Fig.9 The comparison of maximum story drift under rare earthquake 圖10 罕遇地震作用下層剪力最大值優化對比Fig.10 The comparison of maximum story shear force under rare earthquake 4結論 本文在人工魚群算法的基礎上提出一種針對位移型阻尼器位置和參數優化的優化數學模型,并建立了優化算法與有限元軟件的接口, 實現了面向三維建筑結構的位移型阻尼器優化設計。可以直接在實際工程中應用,設計人員僅需根據結構的特征修正目標函數的加權系數及覓食行為中的指導因子即可得到阻尼器的優化布置方案。算例表明了該種優化模型的有效性。 在結構中添加位移型阻尼器后,有時會引起結構層剪力的增加,本文提出一種考慮層剪力的優化目標函數,采用均方根描述結構的響應,能夠更加有效的考慮結構各響應在地震波峰值段的特性。算例驗證了本文優化目標函數的有效性。 實際減震設計時,可根據工程預算確定阻尼器個數,根據結構需求確定阻尼器添加的樓層,運行優化模型,對比不同噸位的優化結果,選擇充分滿足結構適用性和安全性的阻尼器布置方案。 致謝:感謝教育部學術創新團隊“土木抗震減震”和北京市屬高等學校創新團隊建設與教師職業發展計劃項目資助。 參 考 文 獻 [1] Takewaki Ι. Optimal damper placement for minimum transfer functions Earthquake [J]. Engineering and Structural Dynamics,1997, 26(11):1113-1124. [2] Aydin E, Boduroglu M H, Guney D. Optimal damper distribution for seismic rehabilitation of planar building structures[J]. Engineering Structures,2007,29(2):176-185. [3] Mousavi S A, Ghorbani-Tanha A K. Closure to “Discussion on ‘Optimum placement and characteristics of velocity-dependent dampers under seismic excitation’ by SA Mousavi and AK Ghorbani-Tanha” by Izuru Takewaki[J]. Earthquake Engineering and Engineering Vibration,2013, 12(4): 681-682. [4] Singh M P, Moreschi L M. Optimal seismic response control with dampers[J]. Earthquake Engineering & Structural Dy-namics, 2001, 30(4): 553-572. [5] Moreschi L M, Singh M P. Design of yielding metallic and friction dampers for optimal seismic performance [J]. Earthquake Engineering & Structural Dynamics, 2003,32(8): 1291-1311. [6] 李鋼, 李宏男. 位移型耗能減震結構優化設計[J]. 振動與沖擊,2007,26(4):65-68. LI Gang, LI Hong-nan. Optimum design of displacement-based energy dissipative devices [J]. Jouranl of Vibration and Shock,2007,26(4):65-68. [7] Singh M P, Moreschi L M. Optimal placement of dampers for passive response control [J]. Earthquake Engineering & Structural Dynamics, 2002, 31(4): 955-976. [8] 黃銘楓,唐家祥. 高層建筑粘彈性阻尼器的優化設置[J]. 華中科技大學學報,2001,29(11):73-75. HUANG Ming-feng, TANG Jia-xiang. Optimum installation of the viscoelastic dampers[J]. Journal of Huazhong University of Science and Technology,2001,29(11):73-75. [9] 曲激婷,李宏男,李鋼. 位移型消能器在結構減震控制中的位置優化研究[J]. 工程力學,2009,26(1):43-48. QU Ji-ting, LI Hong-nan, LI Gang. Optimal placement of displacement-based energy dissipative devices for passive response control[J]. Engineering Mechanics, 2009,26(1):43-48. [10] 烏蘭,李愛群,沈順高. 基于遺傳算法的偏心結構粘滯阻尼器優化布置研究[J]. 工程抗震與加固改造,2014,36(2):1-7. WU Lan, LI Ai-qun, SHEN Shun-gao. Optimal distribution of viscous damper for eccentric structure by genetic algorithm[J]. Earthquake Resistant Engineering and Retrofitting, 2014,36(2):1-7. [11] 周麗萍,凌云,徐斌. 基于魚群算法的耦合地震作用下鋼結構-控制系統協同優化設計[J]. 工業建筑,2014,44(7):164-169. ZHOU Li-ping, LING Yun, XU Bin. Integrated optimization of steel structure and control system under coupling earthquake based on artificial fish awarm algorithm[J]. Industrial Construction,2014,44(7):164-169. [12] 李亮,遲世春,林皋. 禁忌魚群算法及其在邊坡穩定分析中的應用[J]. 工程力學,2006,23(3):6-10. LI Liang, CHI Shi-chun, LIN Gao. Tabu fish swarm algorithm and its application to slope stability analysis[J]. Engineering Mechanics, 2006,23(3):6-10. [13] 李鋼, 李宏男. 位移型耗能減震結構對框架柱軸力影響的研究[J]. 建筑結構,2009,39(2):25-27. LI Gang, LI Hong-nan. Study on influence of column axial force on the dissipative buildings[J]. Building Structure, 2009,39(2):25-27. [14] 閆維明,王維凝,彭凌云. 不同水準地震作用下鉛阻尼器附加給結構的有效阻尼比及其設計取值研究[J]. 工程力學,2014,31(3):173-180. YAN Wei-ming, WANG Wei-ning, PENG Ling-yun. Study on the additional damping ratio provided by lead dampers and its design values under different earthquake standards[J]. Engineering Mechanics, 2014, 31(3):173-180. [15] GB 50011-2010, 建筑結構抗震規范[S]. 北京: 中國建筑工業出版社, 2010. [16] 李曉磊,邵之江,錢積新.一種基于動物自治體的尋優模式:魚群算法[J].系統工程理論與實踐, 2002, 22(11): 32-38. LI Xiao-lei, SHAO Zhi-jiang, QIAN Ji-xin. An optimizing method based on autonomous animats: fish-swarm algorithm[J]. Systems Engineering-Theory & Practice,2002,22(11): 32-38. Optimization method for the placements and parameters of displacement-based dampers using artificial fish swarm algorithm YAN Wei-ming, GAO Xiao-long, XIE Zhi-qiang, PENG Ling-yun (The College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China) Abstract:In an energy dissipation structure, the seismic mitigation effect of dampers is depended on their parameters and placements. An optimized model based on artificial fish swarm algorithm, was proposed for the optimal design of displacement-based dampers. The model can be applied in structural finite element models with multi dimensions and degrees of freedom to determinate the placements and parameters of displacement-based dampers in each story. In order to deal with the increment of story shear force after installing displacement-based dampers, an optimized objective function was proposed, in which the variation of maximum story-drift angle, story acceleration and story shear force was considered, and the form of root mean square (rms) was adopted to reflect the vibration properties of each story’s responses in the process of earthquake wave excitation more effectively. In the optimal design process of the energy dissipation structure, the weighting coefficients of the objective function can be flexibly adjusted according to the design demands. Some examples were illustrated to verify the effectiveness of the new mathematic model. Key words:dissipative structure; displacement-based dampers; fish swarm algorithm; placement of damper; parameter of damper 基金項目:國家自然科學基金項目(51378039;51421005);北京市教委科技計劃面上項目(KM201110005021) 收稿日期:2015-01-25修改稿收到日期:2015-04-25 通信作者杲曉龍 男,碩士,1990年7月生 中圖分類號:TU352.1 文獻標志碼:A DOI:10.13465/j.cnki.jvs.2016.10.011 第一作者 閆維明 男,博士,教授,1960年7月生