基于果蠅優化算法的自適應隨機共振軸承故障信號檢測方法

崔偉成， 李　偉， 孟凡磊， 劉林密

(海軍航空工程學院 飛行器工程系，山東 煙臺　264001)

基于果蠅優化算法的自適應隨機共振軸承故障信號檢測方法

崔偉成， 李偉， 孟凡磊， 劉林密

(海軍航空工程學院 飛行器工程系，山東 煙臺264001)

摘要：針對傳統自適應隨機共振系統只能單參數優化，而基于群智能算法的自適應隨機共振系統存在優化算法參數選取困難、收斂速度慢的缺陷，提出了基于果蠅優化算法的自適應隨機共振方法。該方法以雙穩隨機共振系統輸出信噪比作為果蠅優化算法的味道濃度，結合二次采樣技術，自適應選取隨機共振系統的結構參數，實現周期信號的特征增強。數據仿真與軸承內圈故障數據分析表明，該方法簡單易行，收斂速度快，能有效的檢測特征信號，實現軸承故障診斷。

關鍵詞：隨機共振；果蠅優化算法；參數優化；軸承故障診斷

1981年Benzi等學者在研究古冰川氣象問題時提出了隨機共振(Stochastic Resonance，SR)的概念[1]，此后隨機共振現象在很多領域受到了廣泛的關注。隨機共振指的是在非線性系統的作用下，噪聲可能起著與人們直覺相反的作用，即一定量的噪聲不僅不會降低系統的輸出響應，在一定程度上還有可能加強系統的輸出響應[1-3]。

隨機共振在信號檢測領域的應用始于小參數(小幅值、小頻率、小噪聲)信號檢測方法的研究，采用二次采樣、參數歸一化等技術處理的隨機共振可處理工程實際中的大參數信號，為其廣泛應用奠定了基礎[3-5]。級聯隨機共振、自適應隨機共振等技術的應用則顯著提高了隨機共振對信號的檢測能力。隨機共振的產生需要對系統參數或噪聲能量進行調節，應用更多的是調節系統參數以達到隨機共振狀態。傳統的自適應隨機共振只針對某一參數進行優化設計，假定其他參數不變，忽略了參數間交互作用[6-9]。為了對系統的多個參數進行同步優化，文獻[8-10]分別采用遺傳算法、粒子群算法及人工魚群算法等群智能算法設計自適應隨機共振系統，在旋轉機械故障信號檢測領域取得了初步進展。但這些優化算法存在參數選取困難、收斂速度慢的缺陷。

本文以周期信號的隨機共振為研究對象，利用果蠅優化算法初始化參數少，易于收斂的優點[11]，選擇雙穩隨機共振系統輸出信噪比作為味道濃度，與二次采樣隨機共振技術結合，對系統結構參數a、b進行同步優化，準確找到最優參數，實現了大參數下周期信號的檢測，可用于軸承故障診斷。

1基本理論

1.1隨機共振

隨機共振現象是非線性系統中噪聲和特征信號的一種協同作用。對最簡單的情形，即非線性系統為雙穩系統，其勢函數為：

(1)

式中，a、b是雙穩系統的結構參數。系統以單頻正弦信號和高斯白噪聲為輸入信號時，對應的郎之萬(Langevin)方程為：

(2)

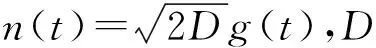
若參數a、b和D相匹配，系統的輸出會按照外力s(t)的調制頻率f0在勢函數的2個勢阱之間進行周期性切換，從而使周期分量得到加強，這就是利用隨機共振實現信號增強的基本原理[1-2]。

在信號檢測領域，添加噪聲D的方法一般不宜采用，實用的方法是調節雙穩系統的結構參數a、b以達到隨機共振狀態。傳統的參數調節方法有單參數調節和參數歸一化兩種。單參數調節方法假定a或b不變，針對另一參數進行優化設計[7]；參數歸一化方法則通過線性變換將a或b歸一，再調節另一參數[8-9]，其本質與單參數調節方法相同。這兩種方法均忽略了參數間的交互作用，不一定能取得最好的效果。僅從提高系統輸出信噪比的角度來說，對參數a，b同步調節的效果更好。

1.2果蠅優化算法

果蠅優化算法(Fruit Fly Optimization Algorithm，FOA)是一種基于果蠅覓食行為推演出的尋求全局優化的新方法，由臺灣學者潘文超提出。果蠅優化算法依照果蠅的覓食行為，將最優解作為食物源，果蠅依靠嗅覺搜索食物氣味并往食物方向飛去， 最終達到逐步逼近食物源的目的[11]。 其步驟如下：

(1) 給定種群規模、最大迭代次數，隨機初始化果蠅群體的位置(X,Y)。

(2) 隨機設置果蠅個體用嗅覺搜尋食物的方向與距離(搜索步長)，得到新的位置(Xi,Yi)。

(3)

(3) 計算果蠅個體與原點之距離，然后計算味道濃度判定值Si。

(4)

式中，Di是果蠅個體與原點之距離。

(4) 將味道濃度判定值Si代入味道濃度判定函數，求出果蠅個體所處位置的味道濃度。

Smelli=fitness(Si)

(5)

式中，Smelli是果蠅個體所處位置的味道濃度，fitness()是味道濃度判定函數。

(5) 求出果蠅群體中味道濃度的極值，并記錄下此果蠅個體的位置。

(6) 果蠅群體利用視覺向步驟(5)記錄的位置飛去，形成新的群聚位置。

(7) 進入迭代尋優，重復執行步驟(2)～(6)，并判斷味道濃度是否優于前一迭代味道濃度，直至迭代次數達到最大迭代數。

相比于其他經常被用作處理最優化問題的群演算法，包括遺傳算法、蟻群算法、粒子群算法等，果蠅優化算法有需優化參數少，計算過程簡單，易于收斂，便于理解等優點。

2果蠅優化算法的自適應隨機共振

基于果蠅優化算法具有隨機、自適應的全局優化能力，本文設計了果蠅優化算法的自適應隨機共振系統，對隨機共振結構參數a、b進行同步優化，其流程見圖1。

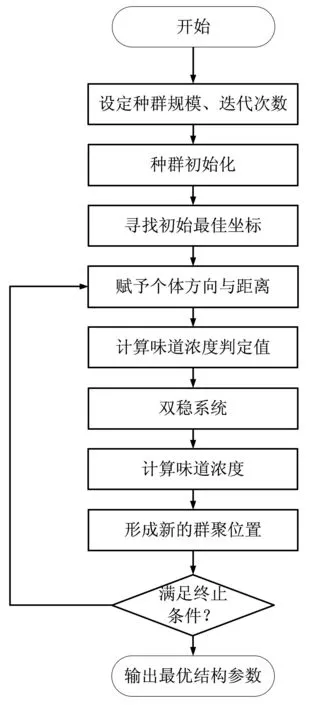
圖1　基于果蠅優化算法的隨機共振流程圖Fig.1 Flowchart of stochastic resonance based on FOA

2.1種群規模及迭代次數確定

種群規模、迭代次數越大，進化得到的解的品質越好，同時計算量也越大，在實際應用中往往做折中處理。

2.2種群初始化

優化參數有2個：a、b，因此設定2個果蠅種群，初始種群采用隨機產生。

2.3味道濃度判斷值縮放

范圍不當的味道濃度判斷值會使果蠅優化算法早熟，從而陷入局部最優。因此，結合隨機共振的參數范圍將味道濃度判斷值進行縮放。對于每次尋優，設置搜索步長，使S的范圍在[0,10]，然后計算果蠅到原點的距離，得到味道濃度判斷值S1i、S2i，按照a=m*S1i，b=n*S2i適當縮放味道濃度判定值以保證a、b的取值范圍。本文取a∈[0,10]，b∈[0,1 000]，因此m=1，n=100。

2.4味道濃度計算

計算味道濃度是果蠅優化算法的基礎。本文定義味道濃度判定函數(適應度函數)為

Smell=fitness(a,b)=SNRout(sr(a,b))

(6)

式中：sr(a,b)是系統的輸出結果；SNRout是系統輸出信噪比，其定義為：

(7)

式中，f0為信號頻率，S(f0)為信號功率，N(f0)為噪聲功率。

2.5尋找初始最佳坐標

坐標初始值的選取一般會影響尋優結果。在工程中常用的隨機共振參數為a=1、b=1，該組參數通常能實現隨機共振。因此，初始最佳坐標的選取以實現a=1、b=1為約束。具體過程為：果蠅位置分別隨機賦值，計算味道濃度判斷值并縮放，得到a、b，若滿足a=1、b=1，則將該位置作為初始最佳坐標；否則，重新隨機賦值，直至a=1、b=1。

2.6迭代尋優

進入迭代尋優過程，保留最佳味道濃度及對應的最佳結構參數值a、b。

2.7迭代終止

迭代終止的條件有兩個：① 迭代次數大于設定閾值；② 找到最佳結果，即味道濃度達到最佳。

果蠅優化算法在尋優的過程中可能陷入局部最優。本文采用添加擾動項的方法避免該問題。具體過程是：

(1)若2代之間的味道濃度之差小于預設精度，即

(8)

式中：Smellz為第z代味道濃度。記錄味道濃度極值Smellex1，進入步驟(2)；否則，進入正常尋優步驟。

(2) 將搜索步長添加擾動項

(9)

式中：r為擾動項累計階數。

(3) 繼續尋優，直至再次尋重新找到味道濃度極值Smellex2。

(4) 若連續兩次的味道濃度極值之差小于預設精度，即

(10)

則尋優結束，迭代終止。否則記

Smellex1=max(Smellex1,Smellex2)

(11)

并進入步驟(2)。

3仿真數據分析

設定雙穩隨機共振系統的輸入信號為u(t)=A0sin(2πf0t)+n(t)。其中，A0=0.2，f0=20 Hz，噪聲n(t)為高斯白噪聲，其均值為0、方差D=2，采樣頻率為fs=5 000 Hz，采樣點數n=4 096。此時，系統的輸入信噪比理論上為SNRin=10lg((A2/2)/(2D))=-23.01 dB，實際信噪比為-25.74 dB。輸入信號的原始時域波形圖及幅值譜分別如圖2(a)、(b)所示。由于強噪聲的加入，在圖2(a)上很難發現周期成分，在圖2(b)上特征頻率點(由于計算誤差的存在，實際為19.53 Hz)的譜線被噪聲淹沒，很難辨認。

在該仿真實例中，輸入信號頻率遠大于1 Hz，通過二次采樣，將其轉化為小參數，再進行果蠅優化自適應隨機共振系統處理[7]。取頻率壓縮率R=1 000，則二次采樣頻率fsr=fs/R=5 Hz，特征頻率壓縮為f0r=f0/R=0.02 Hz。設定果蠅種群規模為20，最大迭代次數為100，適應度精度為0.000 01，擾動項累計階數為5，對二次采樣信號尋找隨機共振系統的最佳參數。

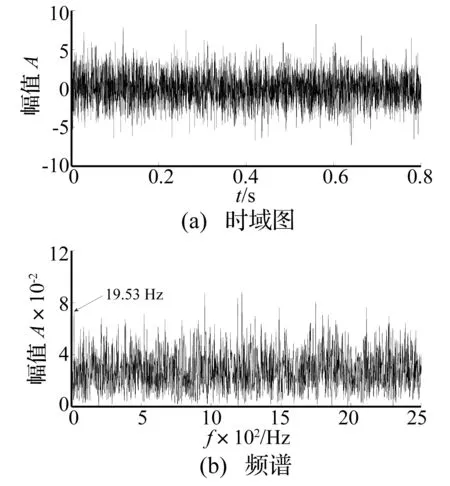
圖2　輸入信號時域波形及頻譜Fig.2 Input signal in time domain waveform and spectrum

經過41次迭代，果蠅優化算法收斂，優化結果為a=0.279 4，b=0.122 6。將二次采樣信號輸入至優化后的隨機共振系統，系統輸出信號的原始時域波形圖及幅值譜如圖3(a)、(b)所示。從圖3(a)可以看出系統輸出在時域上呈現周期性。圖3(b)中的頻率已按照fs=fsr*R、f0=f0r*R還原，為了便于觀察，只畫出了低頻部分。可以看出特征頻率(19.53 Hz)處的譜線存在明顯的峰值。此時，系統的輸出信噪比為SNRout=-8.363 8 dB，較輸入信噪比已大大提高。可見，該方法可有效檢測出微弱正弦信號的特征頻率。

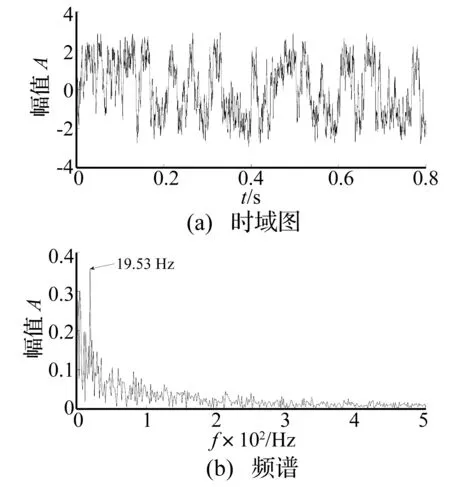
圖3　果蠅優化算法自適應隨機共振系統輸出信號時域波形及頻譜Fig.3 The FOA stochastic resonance system output signal in time domain waveform and spectrum

為了分析果蠅優化算法在隨機共振系統參數自適應調節中的優勢，將之與遺傳算法(GA)和粒子群算法(PSO)進行對比。遺傳算法參數設置為：種群數量20，最大迭代次數100，交叉概率0.7，變異概率0.05。粒子群算法的參數設置為：種群數量20，最大迭代次數100，最大搜索速度為調整步長的10%。仿真數據的優化效果對比見表1。從表1可以看出，三種優化算法均能調整參數達到隨機共振狀態，但果蠅優化算法迭代次數少，在計算速度方面具有優勢，更適合工程應用。

表1　仿真數據的優化效果對比

從優化參數與信號增強的效果來看，三種算法獲得的a、b數值相差較大，但輸出信噪比近似，說明隨機共振在最佳參數附近的信號增強性能對參數不敏感，具有較強的魯棒性。因此，在隨機共振的工程應用中，應綜合考慮輸出響應的提高程度與算法復雜度、計算耗時等因素。

4工程應用

實驗數據來自美國凱斯西儲大學電氣工程實驗室[12]。其實驗選用型號為6205-2RS的深溝球軸承，該軸承的尺寸參數如表2如示。

表2　 滾動軸承6205-2RS的尺寸參數

使用電火花加工技術在該軸承內圈上布置了單點故障，故障直徑為0.177 8 mm，該軸承用于支承電機軸，電機轉速為1 772 r/min，則滾動軸承內圈點蝕故障特征頻率為：

(9)

式中：f0為內圈點蝕故障特征頻率，α為接觸角。

在電機支撐端采用加速度傳感器采集軸承的振動信號，采樣頻率為fs=12 kHz，計算時，采樣點數取n=8 192。

圖4(a)和圖4(b)分別給出了原始采樣信號的時域波形圖和幅值譜。在圖 4(a)的波形圖上可以看出原始信號比較雜亂，且沖擊現象明顯，不易發現周期成分。在圖4(b)的頻譜圖上隱約可以看見滾動軸承內圈故障頻率f0(由于計算誤差的存在，實際為159.7 Hz)處存在譜線。

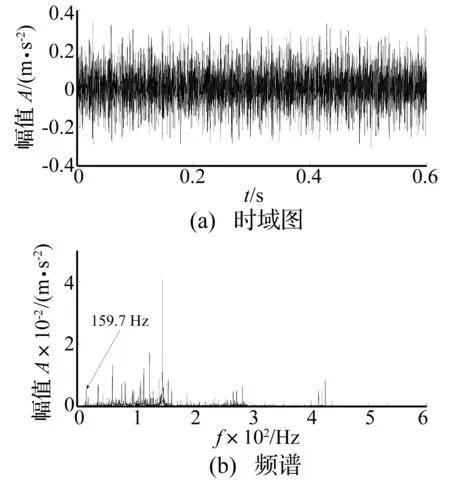
圖4　原始信號時域波形及頻譜Fig.4 The original input signal in time domain waveform and spectrum

取頻率壓縮率R=2 000對原始信號進行二次采樣。二次采樣頻率為fsr=fs/R=6 Hz，特征頻率為f0r=f0/R=0.079 Hz。設定果蠅種群規模為20，最大迭代次數為200，適應度精度為0.000 01，擾動項累計階數為5，對二次采樣信號尋找隨機共振系統的最佳參數。經過75次迭代，算法收斂，輸出的最優參數為a=0.010 0、b=14.296 7。將最優參數代入隨機共振系統，對原始采樣信號進行隨機共振處理，分別得到圖 5(a)、(b)所示的時域波形圖和幅值譜(頻率已還原，且只畫出了低頻部分)。

由圖5(a)可以看出，隨機共振處理后的時域波形中的噪聲成分被極大的削弱了，周期成分已比較明顯。在圖 5(b)中可以非常清楚的看到特征頻率f0(159.7 Hz)處的譜線存在明顯的譜峰，并且特征頻率二倍頻處(319.4 Hz)的譜峰也清晰可見。這與滾動軸承存在內圈故障的事實相吻合。可見，該方法在工程中的應用是可行的。

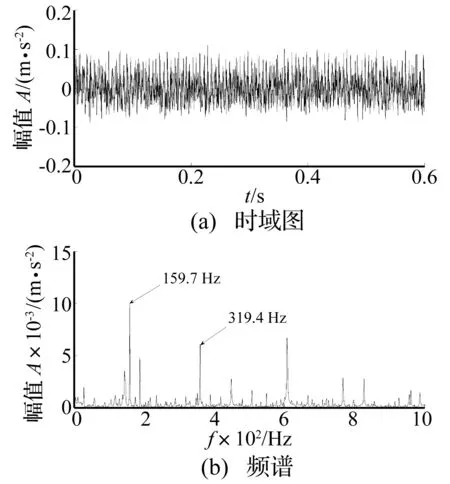
圖5　果蠅優化算法自適應隨機共振系統輸出信號時域波形及頻譜Fig.5 The FOA stochastic resonance system output signal in time domain waveform and spectrum

將果蠅優化算法與遺傳算法(GA)和粒子群算法(PSO)進行對比。其中，遺傳算法、粒子群算法的最大迭代次數設置為200，其他參數設置與前文所述的仿真數據優化的參數一致。優化效果見表3。從表3中的優化的參數來看，三種算法獲得的a數值接近、b數值相差較明顯，但輸出信噪比近似，在此印證了隨機共振的魯棒性，表明三種算法均可用于軸承故障信號檢測；從迭代次數及計算耗時方面可以看出果蠅優化算法在計算成本上的優勢。

5結論

本文提出了一種基于果蠅優化算法的雙參數同步優化自適應隨機共振方法。該方法以系統輸出信噪比作為果蠅優化算法的味道濃度，與二次采樣隨機共振技術相結合，實現了參數的自適應選取。該方法簡單易行，收斂速度快，能有效的檢測軸承故障的特征信號，具有一定的工程應用價值。

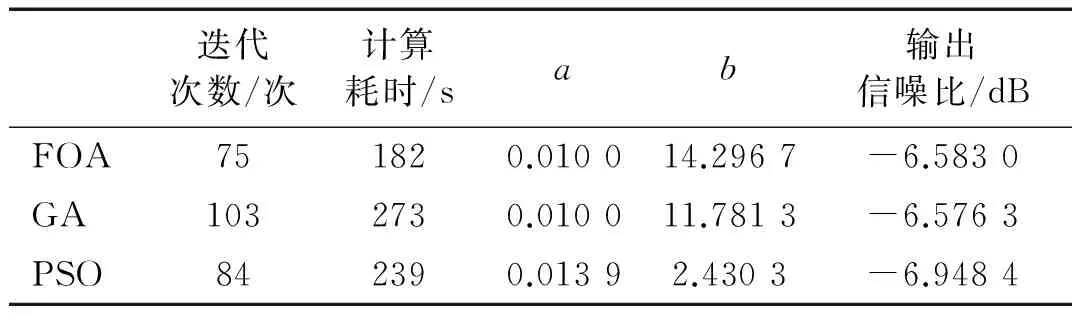
表3　實測數據的優化效果對比

參 考 文 獻

[1] Benzi R, Sutera A, Vulpinai A. The mechanism of stochastic resonance [J]. Journal of Physics A: Mathematical and General, 1981, 14(11): 453-457.

[2] Mcnamara B, Wiesenfeld K, Roy R. Observation of stochastic resonance in a ring laser [J]. Physical Review Letters, 1988, 60(25): 2626-2629.

[3] Li Qiang, Wang Tai-yong, Leng Yong-gang, et al.Engineering signal processing based on adaptive step-changed stochastic resonance [J]. Mechanical Systemsand Signal Processing, 2007, 21(5): 2267-2279.

[4] Li Jian-long，Xu Bo-hou． Effects of signal spectrum varying on signal processing by parameter-induced stochastic resonance[J]. Physica A: Statistical Mechanics and its Applications, 2006, 361(1): 11-23．

[5] 冷永剛，王太勇．二次采樣用于隨機共振從強噪聲中提取弱信號的數值研究[J]．物理學報，2003，52(10) ：2432-2437．

LENG Yong-gang, WANG Tai-yong. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise [J]. Acta Physica Sinica, 2003, 52(10): 2432-2437.

[6] 雷亞國，韓冬，林京，等． 自適應隨機共振新方法及其在故障診斷中的應用[J]． 機械工程學報，2012，48(7): 62-67．

LEI Ya-guo，HAN Dong，LIN Jing，et al． New adaptive stochastic resonance method and its application to fault diagnosis [J]. Journal of Mechanical Engineering,2012,48(7): 62-67.

[7] 陳敏，胡蔦慶，秦國軍，等．參數調節隨機共振在機械系統早期故障檢測中的應用 [J]．機械工程學報，2009，45(4): 131-135．

CHEN Min, HU Niao-qing, QIN Guo-jun, et al. Application of parameter-tuning stochastic resonance for detecting early mechanical faults [J]. Journal of Mechanical Engineering, 2009, 45(4): 131-135.

[8] 王晶，張慶，梁霖，等．采用遺傳算法的自適應隨機共振系統弱信號檢測方法研究 [J]．西安交通大學學報，2010，44(3):32-36．

WANG Jing, ZHANG Qing, LIANG Lin, et al. Adaptive stochastic resonance based on genetic algorithm with applications in weak signal detection [J]. Journal of Xi’an Jiaotong University, 2010, 44(3): 32-36.

[9] 張仲海，王多，王太勇，等．采用粒子群算法的自適應變步長隨機共振研究[J]．振動與沖擊，2013，32(19):125-130．

ZHANG Zhong-hai, WANG Duo, WANG Tai-yong, et al. Self-adaptive step-changed stochastic resonance using particle swarm optimization[J]. Journal of Vibration and Shock, 2013, 32(19):125-130.

[10] 朱維娜，林敏．基于人工魚群算法的軸承故障隨機共振自適應檢測方法 [J]．振動與沖擊，2014，33(6):143-147．

ZHU Wei-na, LIN Min. Method of adaptive stochastic resonance for bearing fault detection based on artificial fish swarm algorithm [J]. Journal of Vibration and Shock, 2014, 33(6):143-147.

[11] Pan Wen-chao. A new fruit fly optimization algorithm: taking the financial distress model as an example [J].Knowledge-Based System, 2012, 29:69-74.

[12] Case Western Reserve University Bearing Data Center [EB/OL].[2011-10-16]http: //csegroups.case.edu/bearingdatacenter.

Adaptive stochastic resonance method for bearing fault detection based on fruit fly optimization algorithm

CUI Wei-cheng, LI Wei, MENG Fan-lei, LIU Lin-mi

(Department of Aircraft Engineering, Naval Aeronautical and Astronautical University,Yantai 264001, China)

Abstract:The traditional adaptive stochastic resonance method can only realize one-parameter optimization, moreover the swarm-aptitude optimization algorithms need to choice appropriate parameters and the convergence speed will slow down with the increase of population. In order to avoid the disadvantages, a new adaptive stochastic resonance method based on the fruit fly optimization algorithm(FOA) was proposed．The output signal to noise ratio of a bi-stable system was taken as a fitness function in FOA, and the parameters were selected adaptively. The analysis of the simulation data and the real fault data of a bearing shows that the new adaptive stochastic resonance method can effectively realize the characteristic signal detection and early fault diagnosis effectively.

Key words:stochastic resonance; fruit fly optimization algorithm; parameter optimization; bearing fault diagnosis

基金項目：國家部委預研基金資助(9140A27020214JB1446)

收稿日期：2015-07-02修改稿收到日期：2015-10-31

中圖分類號:TN911.23；TP206.3

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.10.015

第一作者 崔偉成 男，博士生，講師，1981年6月生