緊鄰建（構）筑物水下爆破振動安全判據研究綜述?

蘇 瑩吳 立彭亞雄周瑞鋒蘇小毛

①武漢科技大學城市學院（湖北武漢，430083）

②中國地質大學（武漢）（湖北武漢，430074）

③湖南創意爆破工程有限公司（湖南長沙，410001）

?

緊鄰建（構）筑物水下爆破振動安全判據研究綜述?

蘇 瑩①②吳 立②彭亞雄②周瑞鋒②蘇小毛③

①武漢科技大學城市學院（湖北武漢，430083）

②中國地質大學（武漢）（湖北武漢，430074）

③湖南創意爆破工程有限公司（湖南長沙，410001）

［摘 要］簡要闡述了水下爆破作用下建（構）筑物安全性能評價指標，綜合分析了振動幅值單因素安全判據在水下爆破緊鄰建（構）筑物安全性能評定中的應用，并介紹了振速-頻率雙因素安全判據理論研究方法及各國安全判定標準，分析討論了兩種判據在爆破振動安全評定考慮因素與應用范圍上的不足。基于累積損傷機理及振動疊加理論，介紹了爆破振動持續時間及微差爆破延時間隔對建（構）筑物安全性能的影響。提出爆破振動安全判據應從爆破振動持續時間及微差爆破延時間隔這兩方面加以完善，并建議在實際工程中采用最佳微差延時間隔以達到最優降振效果。

［關鍵詞］安全判據；振動速度；振動頻率；振動持續時間；微差爆破延時間隔

引言

高強度的爆破振動會使周邊建（構）筑物局部失穩甚至整體破壞［1-2］。因此，必須采用合理的爆破振動安全判據，對緊鄰建（構）筑物的穩定性與安全性進行判斷，使其振動狀態始終處于安全可控的范圍內。水下爆破時緊鄰建（構）筑物受迫振動的主要評價指標包括：振動速度、振動頻率、振動持續時間等［3-4］。工程上多采用爆破質點振速單因素安全判據或綜合考慮振速-頻率的雙因素安全判據［5］。

爆破振速安全判據考慮因素過于單一，不能很好地反映建（構）筑物受迫振動的真實狀態，目前已很少運用于實際工程［6］。振速-頻率的雙因素安全判據考慮了頻率作用下質點安全振速的折減，與單因素判據相比較，更為合理［7-9］。因而，近年來各國在原安全標準基礎上，提出了考慮頻率因素的振速安全標準。

爆破振動持續時間會導致振動疊加，從而影響結構動力響應特征［10］。國內外學者也對此開展了一系列理論研究。凌同華等［11］利用時-能密度法，對微差爆破延期時間進行優化分析，得出爆破振動幅值最小情況下的最優微差延期時間范圍；Aldas等［12］基于對振動疊加理論與微差爆破干擾降振理論的研究，開發了一個系統的爆破振動監測控制體

系。但目前工程領域尚無可指導實踐的統一安全判據，需要繼續進行研究探討。

1 水下爆破安全判據

1. 1 振動幅值單因素安全判據

1. 1. 1 爆破振動強度因子

單因素爆破振動安全判據可以用統一的爆破振動強度因子A來表示，其經驗公式為［13］：

A＝KQαrβ。（1）式中：A為測點所在地質點爆破振動強度因子（振動速度、位移或加速度）；r為爆心至測點之間的距離，m；Q為單段裝藥量，kg；K、α、β為與地質條件有關的系數。

霍永基等［14］研究發現，爆破振動強度因子中，振動速度與建（構）筑物的穩定性與安全性關系更為緊密，對其影響更大，因而在水下爆破工程中，一般采用振動速度來判斷緊鄰建（構）筑物受迫振動的安全性與穩定性。

1. 1. 2 質點爆破振速

質點爆破振速可按Sadaovsk公式求解［15-16］：

式中：v為待測質點爆破振速，cm/ s；ε為與藥量相關的指數；K、α為與地質條件有關的系數，其參考取值如表1所示。

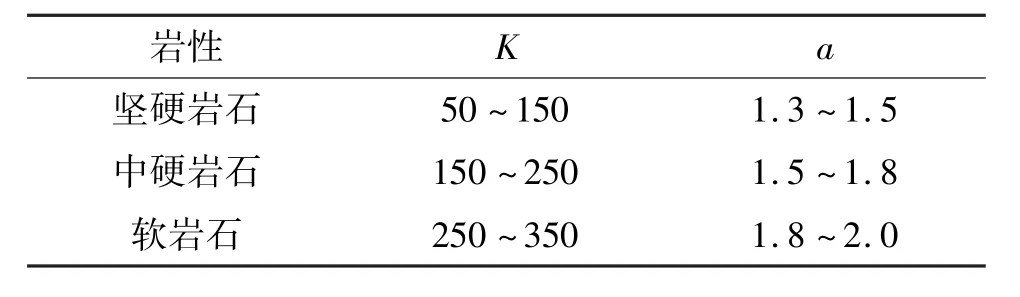
表1 爆區不同巖性的K、α值Tab. 1 Value of K and α under different lithological characters in blasting area

K、α的取值隨著爆破類型、方式的不同而不同；同時，由于實際工程中地質條件復雜多變，該取值多采用現場試驗或回歸分析等方法獲得。ε一般取1/2或1/3［17］。對實測數據分別用ε＝1/2和ε＝1/3進行回歸分析，發現ε＝1/3時，剩余標準差較小，因此，一般情況下，取ε＝1/3較為合理［18-19］。

由于水下爆破振速測量環境與爆破影響因素的復雜性，采用薩達夫斯基公式無法準確得知質點振速。針對水下爆破的特殊性，孟吉復等［20-23］引入高程差因子γ，對傳統薩達夫斯基公式進行修正，修正后質點振速的表達式為：

式中：H為爆破點至測點間的相對高差，m；γ為高差修正系數；K、α和γ取值可采用現場試驗或多組監測數據的回歸分析獲取。

水下爆破工程中，緊鄰建（構）筑物在持續爆破振動作用下的動力響應狀態不僅與爆破振動特性有關，還應當充分考慮結構自身的動力特性［24］。質點振速、振動頻率以及振動持續時間均會對建（構）筑物安全性能判定產生較大影響，因而采用單一的質點振動速度判定結構安全性缺乏合理性［25-27］。目前，國內外多采用振速-頻率雙因素安全判據。

1. 2 振速-頻率雙因素安全判據

1. 2. 1 基于頻率比的折合振速

焦永斌［28］采用頻率比βf計算頻率作用下質點振動折合速度，其表達式為：

式中：vf為頻率作用下地面質點折合振速，cm/ s；βf為頻率效應影響系數；vc為地面質點的振動速度，cm/ s。

βf可通過最小二乘法分析獲得：

式中：Kβ為頻率比例系數；fg為建（構）筑物的自振頻率，Hz；fb為爆破振動作用下地面質點的振動頻率，Hz。

fb/ fg＜5時，Kβ＝1～2，βf＜1，折合振速小于監測值，建（構）筑物在爆破振動作用下不會產生共振，對其安全有利；fb/ fg＞5時，Kβ＝2～4，βf可能等于或者大于1，折合振速大于或等于監測值，可能引發建（構）筑物共振，對其安全不利［29］。

目前，國內對于fb有兩種較為常用的計算方法。焦永斌［28］研究得出fb的計算公式如下：

式中：Kf為與振動頻率相關的系數，Kf＝0. 01～0. 03；cs為巖石的橫波波速，cm/ s。

唐春海等［30］針對不同的爆破形式，得出：

式中：k為與頻率相關的系數，硐室爆破中，k＝0. 8～5. 0；臺階爆破中，k＝5. 0～50. 0；拆除爆破時，k＝1. 0～10. 0。k在其取值范圍內，與Q存在如下關系：Q值較大時，k可取較小值；反之亦反。

折合振速及兩類頻率預測公式均屬于經驗公式，較為粗糙，無法準確判斷建（構）筑物安全性，但仍為爆破振動安全判據做了有益探索，值得借鑒。

1. 2. 2 國內外頻率-振速雙因素安全判據

國內外對于爆破振動安全判據做了一系列探索，結合各國工程經驗與實際抗震設防要求，獲得了符合各國實際的頻率-振速爆破振動安全判據，具體如表2～表5所示［21-32］。

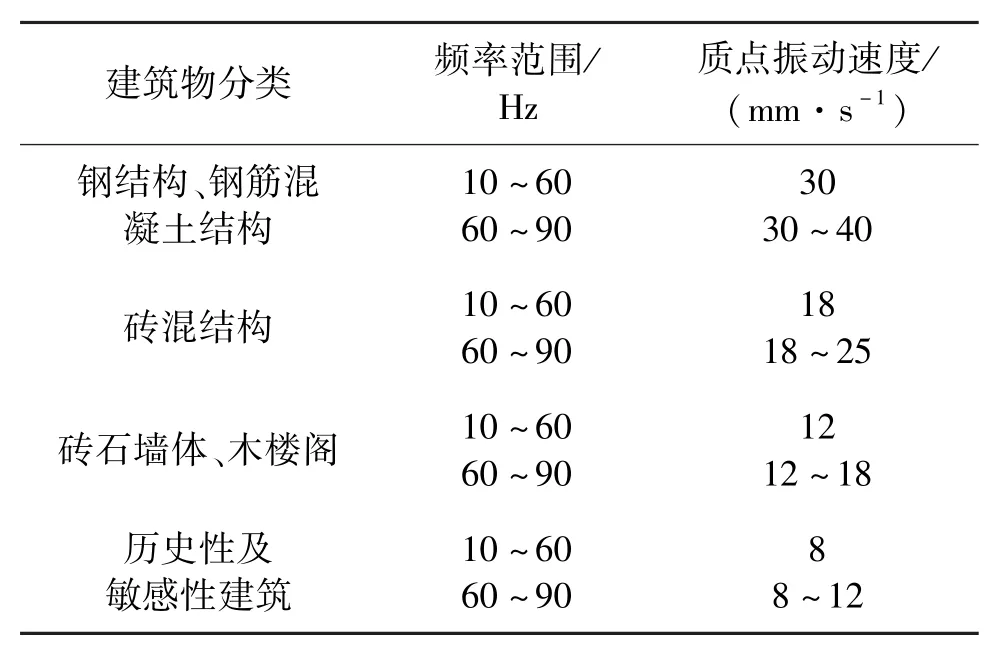
表2 瑞士爆破振動安全判據Tab. 2 Safety criterion of blasting vibration in Switzerland

1. 2. 3 基于頻率-振速因素的工程設計方法

張立國等［33］通過量綱和諧原理及δ定理建立相似準數方程，推導了爆破振動主頻預測公式：

式中：K、α為與傳播介質相關的參數，可通過現場試驗獲得。

工程地質條件與周邊建（構）筑物分布已知時，以頻率-振速雙因素安全標準為控制值，可獲得爆破現場合理振動幅值。結合式（3）與式（8），可獲得同時考慮頻率、振速的最優單段裝藥量。

表3 德國爆破振動安全判據（DIN4150）Tab. 3 Safety criterion of blasting vibration in Germany（DIN4150）

表4 美國露天礦務局標準（OSM標準）Tab. 4 Criterion of the open-pit mine bureau in America（OSM criterion）

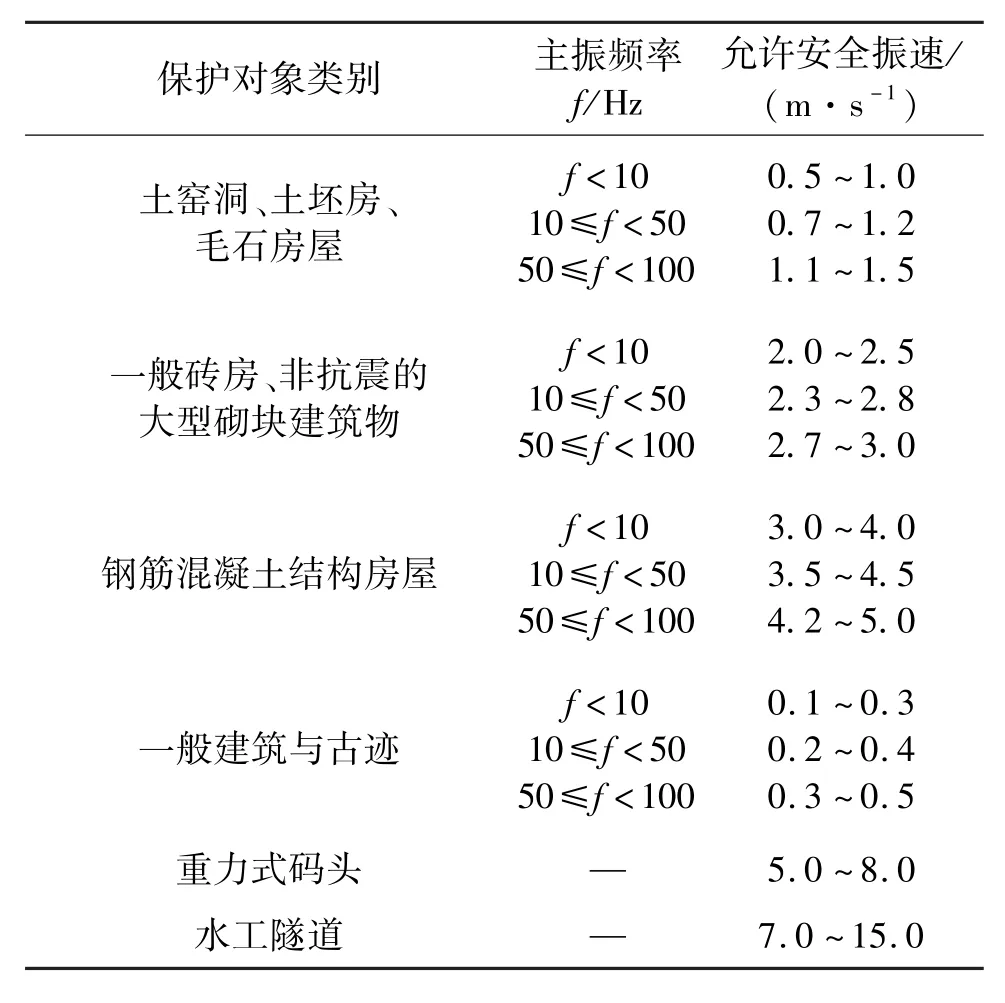
表5 中國爆破振動安全允許標準Tab. 5 Safety criterion of blasting vibration in China

1. 3 考慮振動持續時間的爆破振動安全判據

在持續爆破振動影響下，圍巖裂隙發展直至破壞，同時建（構）筑物振動速度允許值下降（降低2倍以上［34］），嚴重危害圍巖及臨近建（構）筑物安全性能。同時，結構反應超過彈性極限后可能會導致強度有所喪失，其具體表現為：1）線性體系中，結構反應較大值的發生概率隨振動持續時間的上升而上升；2）非線性體系中，振動持續時間的升高也會導致結構內部產生永久變形的概率上升；3）爆破振動作用下，結構物的損壞程度仍將隨振動持續時間的上升而上升。

振動持續時間t與距離r之間的近似關系可表示如下［35］：

高富強等［36］參照薩達夫斯基公式，采用量綱分析得出：

式中：vmax/ r為比例速度，反映的是振動速度幅值與爆心距測點距離之間的定量關系。

振動持續時間由1 s增加至50 s的過程中，爆破能量對于緊鄰結構物的破壞能力平均可增大40倍［35］。從以上結論可以得知，振動持續時間也應當作為水下爆破作用下緊鄰建（構）筑物安全判據的考慮因素之一，但目前國內外暫無相關成果。

1. 4 微差爆破振動疊加效應

1. 4. 1 微差爆破振動疊加理論

微差爆破振動傳播過程中，由于地震波在傳播介質中衰減較慢，一般會產生相互干擾與疊加，與齊發爆破相比，情況更為復雜。微差爆破振動疊加強度的影響因素包括：起爆順序及抵抗線方向、爆心距、微差間隔時間。當爆心與測點之間的距離超過50 m時，不同起爆順序下振動疊加放大系數差別不大［37］。而與之相反的是，爆心距及微差爆破間隔時間這兩個因素對爆破振動疊加放大系數會產生較大的影響。圖1為不同微差爆破間隔時間下振動疊加放大系數與爆心距的關系圖。

由圖1可知，當爆心距較小時，振動疊加系數趨于1，基本未產生振動疊加；當其值增大到一定程度后，爆破振動疊加系數將隨著爆心距的增大而增大。與此同時，振動疊加系數也與微差爆破間隔時間有一定關系。微差爆破間隔時間的不同會引起爆破作用及振動效應的改變［38-41］。

1. 4. 2 最優微差延時間隔

若采用的微差爆破間隔時間趨于合理，爆破振動能夠最大限度地疊加相消［42］。Langefors等［43］研究發現，在爆破振動周期及波形一致的情況下，若將微差爆破間隔時間取為Δt＝T/2（T為振動周期），可以最大限度地使爆破振動干擾相消，從而達到最佳降振效果。然而，實際微差爆破相鄰段爆破振動的干擾并非簡單疊加，而應當綜合考慮實際地質條件及爆破方案等諸多因素的影響［44］。

沈伯騫［45］推導出的微差爆破相較于同條件下齊發爆破的爆破振動效應降低系數求解公式為：

式中：B為微差爆破地震效應的降低系數；An為微差爆破振幅；Aji為齊發爆破振幅；n為微差爆破的段數；Δt為微差起爆的延遲時間，ms；ω為巖層的自振頻率，Hz。

B值越小，說明微差爆破延時間隔的取值對于減振更為有利。當式（11）分子部分取0時，將獲得最佳減振效果。故最優微差延時間隔的求解公式如下：

2 問題與思考

1）采用水下爆破作用下地面質點振動速度單因素安全判據在某種程度上能夠判定建（構）筑物安全性，但卻具有很大的局限性。其原因在于：建（構）筑物安全性能影響因素很多，建（構）筑物自身動力特性、起爆方式、地震波傳遞介質等都會對其產生較大影響［46-49］。地面質點振動速度相同，振動頻率及振動持續時間差別較大時，建（構）筑物實際所處狀態會與單因素判據評估結果相距甚遠［50］。因而，振動頻率及振動持續時間對建（構）筑物安全性能的影響是不容忽視的，需要加大研究力度，形成可運用于實踐的多因素統一安全判據。

2）國內外日漸普及的振速-頻率雙因素安全判據是在實踐過程中形成的修正判據，與單因素相比更具合理性，但仍存在一定缺陷。其一，工程領域已開始采用考慮爆破振動頻率與爆破振速協同作用的雙因素安全判據對以房屋為主的建筑物在爆破振動作用下的安全性能進行判定，但對于結構動力響應復雜的建（構）筑物（巖石邊坡、洞室圍巖和新澆混凝土等）卻無可供參考的雙因素安全判據［51］；其二，雙因素安全判據未考慮振動持續時間對建（構）筑物動力特性的影響，考慮因素不夠全面，對建（構）筑物在爆破振動作用下的安全判定有失準確［52］；其三，在水下爆破實踐中，由于水環境較陸地環境復雜，影響因素繁多，該判據在水下爆破工程中的適用性還有待考察［53-54］。因而，該安全準則的廣度與深度還需要在實踐中補充強化。

3）目前工程領域對于爆破振動持續時間的研究仍停留于理論層面，未與振動速度及振動頻率聯系起來，無法用于準確判定建（構）筑物安全性能。同時，在微差爆破過程中，間隔時間的不同會在中遠區產生不同程度的疊加，直接影響建（構）筑物安全性能，因而微差爆破間隔時間也應當考慮在爆破振動安全判據內［55］。在工程實踐中，可運用微差爆破振動疊加理論和建（構）筑物累計損傷機理，選擇降振效果最佳的微差爆破時間，從而減小微差爆破振動疊加對建（構）筑物安全性能的影響［56-57］。

3 結論

1）質點振動速度單因素安全判據考慮因素單一，對建（構）筑物的安全判定結果與其實際所處狀態相差較大，應減少其工程應用。

2）振速-頻率雙因素安全判據是對前者的修正，具有一定合理性，但未體現出振動持續時間對結構安全性能的影響，且多應用于房屋為主的建筑物，水下環境適用性也有待考察。

3）爆破振動持續時間會使建（構）筑物在反復的水下爆破振動沖擊作用下產生累計損傷，有必要將其列入安全判據范疇，對相關行業標準進行修正，并運用于工程實踐。

4）微差爆破會在中遠區產生振動疊加，影響建（構）筑物安全性能，需要在安全判據中加以考慮，并在實際工程中采用最佳微差爆破間隔時間，達到最優降振效果。

參考文獻

［1］ JONES J P，WHITTIER J S. Waves at a flexibly bonded interface［J］. Journal of Applied Mechanics，1967，34 （4）：905-909.

［2］ SCOTT D F，WILLIAMS T J，DENTON D K，et al. Seismic tomography as a tool for measuring stress in mines ［J］. Mining Engineering，1999，51（1）：77-80.

［3］ 石崇，畢衛國.爆破地震破壞判據的探討［J］.巖土力學，2004，25（增刊）：115-118. SHI C，BI W G. Discussion of blasting damage criteria ［J］. Rock and Soil Mechanics，2004，25（Suppl.）：115-118.

［4］ 陽生權，廖先葵，劉寶琛.爆破地震安全判據的缺陷與改進［J］.爆炸與沖擊，2001，21（3）：223-228. YANG S Q，LIAO X K，LIU B C. Default of the judging standard of blasting vibration safety abstract［J］. Explosion and Shock Waves，2001，21（3）：223-228.

［5］ 言志信，王永和，江平，等.爆破地震測試及建筑結構安全標準研究［J］.巖石力學與工程學報，2003，22 （11）：1907-1911. YAN Z X，WANG Y H，JIANG P，et al. Study on measurement of blast-induced seism and building safety criteria［J］. Chinese Journal of Rock Mechanics and Engineering，2003，22（11）：1907-1911.

［6］ 汪旭光，于亞倫.關于爆破震動安全判據的幾個問題［J］.工程爆破，2001，7（2）：88-92. WANG X G，YU Y L. On several problems of safety criterion for blasting vibration［J］. Engineering Blasting，2001，7（2）：88-92.

［7］ 程康，徐學勇.爆破振動頻率對振動效應影響的試驗研究［J］.爆破，2003，20（3）：79-81. CHENG K，XU X Y. Experimental Research on influence of blasting vibration frequency on its vibration effect［J］. Blasting，2003，20（3）：79-81.

［8］ 李孝林，穆太升，董鑫，等.頻率在爆破震害中的作用及其影響因素分析［J］.工程爆破，2001，7（3）：15-18. LI X L，MU T S，DONG X，et al. Role of frequency in harm of blasting vibration and analysis on its influence factors［J］. Engineering Blasting，2001，7（3）：15-18.

［9］ 陶劉群，于亞倫.爆破振動安全判據三大核心問題研究［J］.金屬礦山，2012（10）：127-129. TAO L Q，YU Y L. Research of three key issues on safety standards of blasting vibration［J］. Metal Mine，2012 （10）：127-129.

［10］ 陽生權.爆破地震累積效應理論和應用初步研究［D］.長沙：中南大學，2002. YANG S Q. Study on theory and application of blasting vibration cumulative effect［D］. Changsha：Central South University，2002.

［11］ 凌同華，李夕兵，王桂堯.爆破震動災害主動控制方法研究［J］.巖土力學，2007，28（7）：1439-1442. LING T H，LI X B，WANG G Y. A study on initiative control of blast vibration damages［J］. Rock and Soil Mechanics，2007，28（7）：1439-1442.

［12］ ALDAS G G U，ECEVITOGLU B. Waveform analysis in mitigation of blast-induced vibrations［J］. Journal of Applied Geophysics，2008，66（1/2）：25-30.

［13］ 黃樹棠，張雪亮.爆破地震效應［M］.北京：地震出版社，1981.

［14］ 霍永基，王湘均，費驥鳴.爆破地震效應及安全評定方法［M］/ /中國力學學會工程爆破專業委員會.土巖爆破文集（第二輯）.北京：冶金工業出版社，1985.

［15］ 中華人民共和國國家質量監督檢驗總局，中國國家標準化管理委員會.爆破安全規程：GB6722—2014 ［S］.北京：中國標準出版社，2015. General Administration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China，Standardization Administration of the People’s Republic of China. Safety regulations for blasting：GB6722—2014 ［S］. Beijing：China Standard Press，2015.

［16］ 長江重慶航道工程局.水運工程爆破技術規范：JTS204—2008［S］.北京：人民交通出版社，2008. Changjiang Chongqing Waterway Engineering Bureau. Technical code of blasting for port and waterway engineering：JTS204—2008［S］. Beijing：China Communications Press，2008.

［17］ LOPEZ J C，LOPEZ J E，JAVIER F. Drilling and blasting of rocks［M］. Rotterdam，Netherlands：AA Balkema，1995：1-150.

［18］ 趙明生，梁開水，曹躍，等.爆破地震作用下建（構）筑物安全標準探討［J］.爆破，2008，25（4）：24-27. ZHAO M S，LIANG K S，CAO Y，et al. Discussion on the security criteria of construction（structure）of building under blasting vibration［J］. Blasting，2008，25 （4）：24-27.

［19］ 言志信，吳德倫，王漪，等.地震效應及安全研究［J］.巖土力學，2002，23（2）：201-203. YAN Z X，WU D L，WANG Y，et al. The study of blast vibration effect and safety［J］. Rock and Soil Mechanics，2002，23（2）：201-203.

［20］ 孟吉復，惠鴻斌.爆破測試技術［M］.北京：冶金工業出版社，1992.

［21］ 唐海，李海波.反映高程放大效應的爆破振動公式研究［J］.巖土力學，2011，32（3）：820-824. TANG H，LI H B. Study of blasting vibration formula of reflecting amplification effect on elevation［J］. Rock and Soil Mechanics，2011，32（3）：820-824.

［22］ 周同嶺，楊秀甫，翁家杰.爆破地震高程效應的實驗研究［J］.建井技術，1997，18（增刊）：31-35.

［23］ 李春軍，吳立，付海濤，等.基于AHP-Fuzzy法的水下爆破設計方案優選［J］.爆破器材，2015，44（4）：45-50. LI C J，WU L，FU H T，et al. Design optimization of underwater blasting based on AHP-Fuzzy method［J］. Explosive Materials，2015，44（4）：45-50.

［24］ 魏海霞.爆破地震波作用下建筑結構的動力響應及安全判據研究［D］.青島：山東科技大學，2010. WEI H X. Study on dynamic response and safety criterion of buildings to blasting vibration waves［D］. Qingdao：Shandong University of Science and Technology，2010.

［25］ 許紅濤，盧文波.幾種爆破震動安全判據［J］.爆破，2002，19（1）：8-10. XU H T，LU W B. Advance on safety criterion for blasting vibration［J］. Blasting，2002，19（1）：8-10.

［26］ LONGERFORS U，WESTERBERG H，KIHLSTR?M B. Ground vibrations in blasting［J］. Water Power，1958：335-421.

［27］ 余永強，楊小林，梁為民.爆破開挖的振動效應與安全判據［J］.金屬礦山，2008（2）：35-39. YU Y Q，YANG X L，LIANG W M. Vibration effect and safety criteria of blasting excavation［J］. Metal Mine，2008（2）：35-39.

［28］ 焦永斌.爆破地震安全評定標準初探［J］.爆破，1995（3）：45-47.

［29］ 胡冬冬，程康，劉陽，等.頻率因素對爆破振動影響的分析探討［J］.爆破，2012，29（4）：127-130. HU D D，CHENG K，LIU Y，et al. Discussion of blasting vibration effect on frequency factor condition［J］. Blasting，2012，29（4）：127-130.

［30］ 唐春海，于亞倫，王建宙.爆破地震動安全判據的初步探討［J］.有色金屬，2001，53（1）：1-4. TANG C H，YU Y L，WANG J Z. Elementary study of safety criterion for blasting vibration［J］. Nonferrous Metals，2001，53（1）：1-4.

［31］ 劉先鋒，況龍川，孔凡林，等.爆破震動安全判據評述［J］.四川建筑科學研究，2010，36（5）：153-155. LIU X F，KUANG L C，KONG F L，et al. Review of safety criterion for blasting vibration［J］. Sichuan Building Science，2010，36（5）：153-155.

［32］ 劉殿中.工程爆破實用手冊［M］.北京：冶金工業出版社，1999.

［33］ 張立國，龔敏，于亞倫.爆破振動頻率預測及其回歸分析［J］.遼寧工程技術大學學報，2005，24（2）：187-189. ZHANG L G，GONG M，YU Y L. Forecast and regression analysis of blasting vibration frequency［J］. Journal of Liaoning Technical University，2005，24（2）：187-189.

［34］ 張志呈.爆破地震參量與振動持續時間［J］.四川冶金，2002（3）：1-4.

［35］ 李的林，高振儒，朱立新.爆破震動危害中幾個重要因素分析［J］.工程爆破，1999，5（3）：64-67. LI D L，GAO Z R，ZHU L X. Analysis on several principal factors of blasting vibration hazards［J］. Engineering Blasting，1999，5（3）：64-67.

［36］ 高富強，侯愛軍，楊小林，等.基于量綱理論的爆破振動持續時間分析［J］.金屬礦山，2010（9）：143-145. GAO F Q，HOU A J，YANG X L，et al. Analysis of blasting vibration duration based on dimension theory ［J］. Metal Mine，2010（9）：143-145.

［37］ 甄育才，朱傳云.中遠區微差爆破振動疊加效應影響因素分析［J］.爆破，2005，22（2）：11-16. ZHEN Y C，ZHU C Y. Analysis on influential factors of vibration superposition in middle and far field of millisecond blasting［J］. Blasting，2005，22（2）：11-16.

［38］ 宗琦，劉積銘，徐穎.合理延遲時間的理論分析和試驗研究［J］.中國礦業大學學報，1998，27（1）：86-89. ZONG Q，LIU J M，XU Y. Theoretical analysis and experiment research on reasonable delay time of millisecond blasting［J］. Journal of China University of Mining & Technology，1998，27（1）：86-89.

［39］ 吳騰芳，王凱，倪榮福.微差爆破間隔時間計算模型的探討［J］.工程爆破，1997，3（4）：59-62. WU T F，WANG K，NI R F. Study on calculating models of interval time in millise-cond blasting［J］. Engineering Blasting，1997，3（4）：59-62.

［40］ 蘇華友，陸文.微差爆破間隔時間合理性分析［J］.四川冶金，2000（3）：15-17.

［41］ 張丹，段恒建，曾福洪.分段爆破地震強度的試驗研究［J］.爆炸與沖擊，2006，26（3）：279-283. ZHANG D，DUAN H J，ZENG F H. Experimental study on subordinate blasting seismic intensity［J］. Explosion and Shock Waves，2006，26（3）：279-283.

［42］ WHEELER R M. How millisecond delay periods may enhance or deduce blast vibration effects［J］. Mining Engineering，1998，40（10）：969-973.

［43］ LANGEFORS U，KIHLSTR?M B. The modern technique of rock blasting［M］. Stockholm：Almqvist & Wiksell，1963.

［44］ 郭學彬，張繼春，劉泉，等.微差爆破的波形疊加作用分析［J］.爆破，2006，23（2）：4-8，49. GUO X B，ZHANG J C，LIU Q，et al. Analysis of waveform superimposed action of millisecond blasting［J］. Blasting，2006，23（2）：4-8，49.

［45］ 沈伯騫.微差爆破最佳微差時間的計算［J］.遼寧師院學報（自然科學版），1978（1）：29-35.

［46］ MOORE A J，RICHARDS A B，GAD E F，et al. Structural response of brick veneer houses to blast vibration ［C］/ / Proceedings of the 29th Annual Conference on Explosives and Blasting Technique. Nashville，Tennessee，USA，2003：223-230.

［47］ MYER L R，PYRAK-NOLTE L J，COOK N G W. Effects of single fracture on seismic wave propagation ［J］. Rock Joints，1990，15：467-473.

［48］ ADWARDS A T，NORTHWOOD T D. Experimental studies of the effects of blasting on structures［J］. Engineer，1960，210：538-546.

［49］ DUVALL W I，FOGELSON D E. Review of criteria for estimating damage to residences from blasting vibration：BM-RI-5968［R］. Washington：U-S-Bureau of Mines Report Investigation，1962：59-68.

［50］ 羅憶，盧文波，陳明，等.爆破振動安全判據研究綜述［J］.爆破，2010，27（1）：14-22 . LUO Y，LU W B，CHEN M，et al. View of research on safety criterion on blasting vibration［J］. Blasting，2010，27（1）：14-22.

［51］ 盧文波，李海波，陳明，等.水電工程爆破振動安全判據及應用中的幾個關鍵問題［J］.巖石力學與工程學報，2009，28（8）：1513-1520. LU W B，LI H B，CHEN M，et al. Safety criteria of blasting vibration in hydropower engineering and several key problems in their application［J］. Chinese Journal of Rock Mechanics and Engineering，2009，28（8）：1513-1520.

［52］ FARNFIELD R A. Environmental effect of blast-recent experience［J］. International Mining & Mineral，1998，1 （4）：94-99.

［53］ 陳春歌，申志兵，張賢凱，等.水下爆破沖擊波危害及安全控制措施的模擬分析［J］.安全與環境工程，2011，18（1）：58-61. CHEN C G，SHEN Z B，ZHANG X K，et al. Simulation of underwater explosion shock hazards and safety control ［J］. Safety and Environmental Engineering，2011，18 （1）：58-61.

［54］ 張占峰.復雜城市環境下水下鉆孔爆破安全控制研究［D］.廣州：華南理工大學，2013. ZHANG Z F. Study on safety control of underwater drilling blasting under the complex urban environment ［D］. Guangzhou：South China University of Technology，2013.

［55］ 李彬峰.爆破地震效應及其控制措施分析［J］.爆破，2003，20（2）：83-85. LI B F. Analysis of controlling measurement and blasting vibration effect［J］. Blasting，2003，20（2）：83-85.

［56］ 張藝峰，姚道平，謝志招，等.爆破地震效應主控因素分析及減震措施探討［J］.巖土力學，2010，31（1）：304-308. ZHANG Y F，YAO D P，XIE Z Z，et al. Analysis of master control factor of blasting seismic effect and discussion on shock absorption measures［J］. Rock and Soil Mechanics，2010，31（1）：304-308.

［57］ MA G C，MIYAKE A，OGAWA T，et al. Study on the numerical simulations of the blasting and the reduction of vibrations in blasting demolition［J］. Journal of the Japan Explosives Society，1995，56（1）：33-43.

Research Review on Safety Criterion of Underwater Blasting Nearby Constructions

SU Ying①②，WU Li②，PENG Yaxiong②，ZHOU Ruifeng②，SU Xiaomao③

①City College，Wuhan University of Science and Technology（Hubei Wuhan，430083）
②China University of Geoscieneces（Wuhan）（Hubei Wuhan，430074）
③Hu’nan Chuangyi Blasting Engineering Co.，Ltd.（Hu’nan Changsha，410001）

［ABSTRACT］ Evaluation indexes for the safety performance of structures under the underwater blasting were briefly expounded，and the application of the single vibration amplitude criterion to the safety performance evaluation under this circumstance was analyzed. Besides，the theoretical research methods of the dual-factor vibrating velocity-frequency safety criterion as well as the national current standards were introduced. From the above，the lack of the consideration and application scope of both criterions in the safety performance evaluation of blasting vibration was discussed. Based on the cumulative damage mechanism and the vibration superposition theory，the effect that the blasting vibration duration and the differential blasting delay interval result in the safety performance of structures was studied. It was proposed that the safety criterion of blasting vibration should be improved from two aspects，the blasting vibration duration and differential blasting delay interval，and the ideal millisecond delay intervals should be applied in practical engineering to achieve optimal effect of vibration reduction.

［KEY WORDS］ safety criterion；vibration velocity；vibration frequency；vibration duration；delay interval of differential blasting

收稿日期：［分類號］ TD235?2015-07-18

doi：10. 3969/ j. issn. 1001-8352. 2016. 03. 012

基金項目：湖北省科技廳自然基金重點基金項目（2013CFA110）；中國地質大學（武漢）教學實驗室開放基金（SKJ2014065）

作者簡介：蘇瑩（1991 -），女，碩士，主要從事工程爆破、圍巖動力響應方面的研究。E-mail：18672765612@163. com

通信作者：吳立（1963 -），男，教授，博導，主要從事工程爆破、圍巖動力響應方面的研究。E-mail：lwu@ cug. edu. cn