重視變式訓練拓展學生思維

◇　山東　楊　希

?

重視變式訓練拓展學生思維

◇山東楊希

變式訓練的核心是通過變式的構造,將數學知識生成和發展的演變過程表示出來,并將解題思路和易錯點揭示給學生．通過變式訓練的設置,我們可以增加標準試題中的干擾因素,增強學生解題的邏輯思維能力,提高學生分析問題、解決問題的能力．同時,變式訓練也有效提高了數學訓練效率,實現了新課改要求的減負目標．在本文中,我們將從高中數學實踐角度出發,對數學訓練中的變式訓練進行探討,實現對學生數學思維的拓展訓練．

1本質不變,更換表述

在傳統的高中數學訓練中,我們往往采用題海戰術,但這樣的訓練方式不僅枯燥,而且缺乏高效性．有些學生做了大量數學題,但一碰到新題時還是無從下手,很多時候題目只是換了一種說法,就給解題帶來了阻礙．對此,我們在變式訓練實施過程中,采取本質不變、更換表述的形式,深化學生對變式習題的認識．

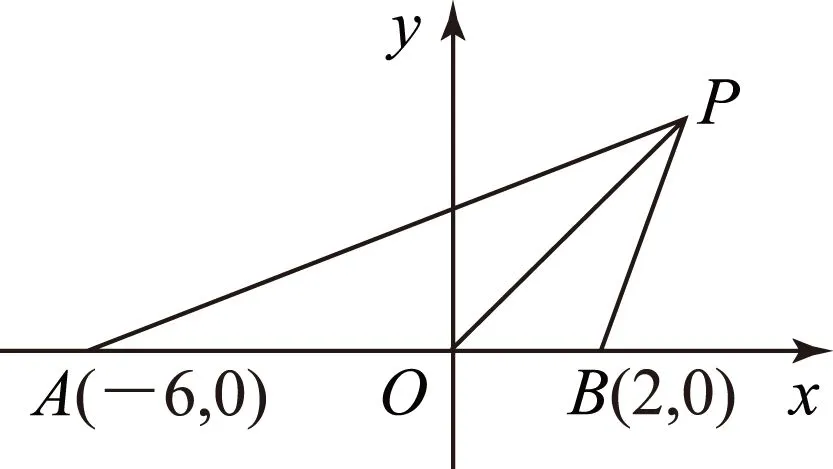
圖1

變式過點A(-6,0)的動直線l1與過點B(2,0)的動直線l2和x軸圍成的△PAB中,PO始終平分∠APB,試求點P的軌跡方程．

很多學生做到這里就終止了,細心的同學可以發現我們還缺乏對定義域的判定．當方程過原點時,點P與原點重合,故可知x≠0．由于題意可知,當點P落于x軸上除線段AB以外的任意一點處均有∠APO=∠BPO=0．所以,這也是本題成立的一種特殊情況,即在方程y=0(x<-6及x>2)時成立．故本題的最終答案即上述二者的綜合．

通過此類換湯不換藥的變式訓練,學生們對題目表述的認識越發深刻,審題及解題思路越發清晰．

2題設不變,改變解法

變式訓練不僅指對題目的改變,針對相同的一道習題使用不同的解法,同樣可以實現變式訓練的目的,也就是我們所說的一題多解．通過一題多解式的變式訓練,可以激發學生數學解題的潛能與積極性,對學生創新能力及綜合能力的培養作用顯著．在日常的高中數學教學中,我們不妨利用相同的題目,通過解法的變化達到有效的變式訓練作用．

設函數g(x)=x2+2x+a，則g(x)在[1,+∞)遞增,由二次函數的性質可知,在x=1時,gmin(x)=3+a．此時,要想保證x2+2x+a>0恒成立,即是要保證3+a>0,最終可以得到a>-3．

方法2在法1的基礎上,對x2+2x+a>0的形式進行改編,由原式恒成立進一步可得a>-x2-2x恒成立．故可得a>h(x)=-x2-2x,在x∈[1,+∞)時恒成立．而在該定義域內,hmax(x)=-3,故a的取值范圍是(-3,+∞)．

方法3首先對函數表達式進行化簡,即

在定義域x∈[1,+∞)中,當a≥0時函數f(x)的值恒為正;當a<0時,函數f(x)為增函數,故x=1時函數可以取到最小值fmin(x)=3+a,當且僅當3+a>0時恒成立,即是a>-3．

從本題的求解來看,面對相同的一道題目,我們采取了多樣化的求解方式．在實際訓練過程中,我們同樣可以采用類似的一題多解變式訓練,幫助學生拓展自身的解題思維．

3逐層深入,改變提問

高中數學變式訓練的核心在于變式構造,將數學問題發展演變的思路揭示給學生．在日常的變式訓練中,我們最常使用的就是遞進式變式,通過對提問難度的逐層增加,實現變式訓練在數學思維與解題方法上的教學目的．

變式已知sin4x+cos4x=23/32,試求sinx-cosx的值．

sin4x+cos4x+2sin2xcos2x=1,

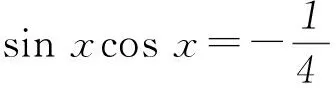
題目經過變式改編后,其難度得到了適當提高．首先由關系式sin4x+cos4x=23/32可得

(sin2x+cos2x)2-2sin2xcos2x=23/32,

即sinxcosx=±3/8．

然后針對2個值進行討論分析:

當sinxcosx=3/8時,

當sinxcosx=-3/8時,

雖然只是小小的改變,但題目的難度和復雜性卻得到了顯著提高,此類變式可以在數學復習階段廣泛采用,可以顯著提高習題課的效率．

總之,在高中數學訓練中,很多問題都是同根同源的．在訓練設計上,我們必須秉承新課改理念,優化變式訓練實效性,在實際教學過程中有目的、有原則、有方法地推進變式訓練在高中數學解題中的使用．唯有從學生角度出發,實施綜合性、創新性的變式教學,才是拓展學生思維的有效方式．

(作者單位：山東省淄博市周村區實驗中學)