矢量控制反坦克導彈頂攻彈道模型
李永盛,李經瑋,權維利,張 可
(航天科工六院四十一所,內蒙古 呼和浩特 010010)
?
矢量控制反坦克導彈頂攻彈道模型
李永盛,李經瑋,權維利,張可
(航天科工六院四十一所,內蒙古 呼和浩特010010)
摘要:針對目前頂攻反坦克導彈矢量控制主要集中在單一的燃氣舵矢量控制的不足,提出了空氣動力和燃氣動力共同作用下的矢量控制反坦克導彈頂攻彈道模型。該模型包括典型頂攻彈道7個階段的數學模型,各階段模型分別表述了所對應階段的彈道設計方案和力學模型。通過建立simulink程序進行了彈道仿真計算,并進行了風洞試驗和發射試驗,仿真與試驗結果表明,建立的數學模型準確可靠。
關鍵詞:反坦克導彈;頂攻彈道;矢量控制
0引言
反坦克導彈矢量控制主要指通過改變發動機燃氣方向,從而改變發動機的推力來控制導彈飛行方向和姿態角,目前國內外頂攻反坦克導彈矢量控制以燃氣舵矢量控制為主。國內對燃氣舵矢量控制在反坦克導彈的研究和應用與世界先進水差距較大,主要研究集中在燃氣舵氣動特性、響應特性等方面。文獻[1]提出了燃氣舵引入對彈體特性的影響,文獻[2]針對繼電式燃氣舵矢量控制反坦克導彈的問題,提出了重力補償方法,并進行了仿真驗證。目前,國內對于燃氣舵和空氣舵復合控制下的力學數學模型研究較少,主要集中于單一的燃氣舵矢量控制。本文針對此問題,提出了空氣動力和燃氣動力共同作用下的矢量控制反坦克導彈頂攻彈道模型。
1氣動模型
1.1軸向力和法向力
氣動模型采用體軸系,在主動段(發動機工作)時,軸向力包括前體軸向力和部分底部軸向力系數,法向力包括攻角產生的法向力、舵偏角產生的法向力以及燃氣舵產生的法向力。由于燃氣舵的存在,發動機推力有損失。燃氣舵氣動力系數通過風洞試驗測試(如圖1所示)。軸向力、法向力和發動機推力如下:
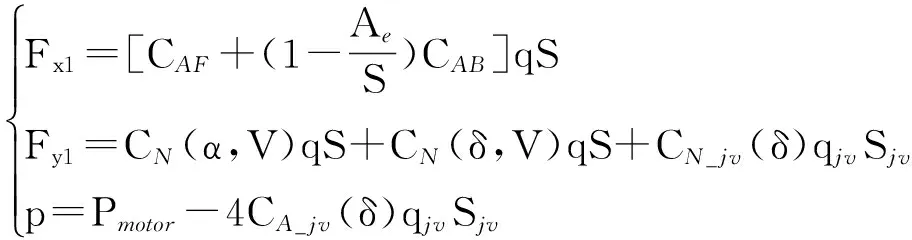

圖1 燃氣舵的流場紋影照片Fig.1 Schlieren of flow field whin vector
在被動段(發動機停止)為前體軸向力系數CAF與底部軸向力系數CAB之和,法向力為包括攻角產生的法向力、舵偏角產生的法向力。軸向力和法向力如下:
1.2舵偏角解算
導彈氣動舵與燃氣舵為1∶1偏轉[2],按照飛行發動機工作前、飛行發動機工作、飛行發動機熄火,舵偏角的解算可分為:
2各階段物理、數學模型
彈道模型基于“瞬時平衡”假設,根據目標與導彈距離可將導彈飛行過程分為多個階段,末段為比例攻擊階段。典型頂攻彈道分為以下7個階段。
2.1前滑塊未離軌
前滑塊未離軌前,導彈在發射筒內為直線加速運動狀態。由于速度小于16m/s,可以忽略氣動力。摩擦力系數μ=0.25。該階段數學模型如下所示:

該階段為無控過程,導彈運動僅為一個自由度,實測結果與仿真結果非常吻合。
2.2前滑塊離軌,后滑塊未離軌
當導彈前滑塊離軌后,由于重力對重心產生力矩,導彈繞后滑塊質點旋轉。由于速度小于15m/s,阻力不超過1N,該階段忽略氣動阻力和升力。

圖2 受力分析Fig.2 Force analysis
如圖2所示,由于導彈繞后滑塊旋轉,沒有采用“瞬時平衡”假設,以尾噴口中心為研究對象,以發射筒軸向進行力分解,所受的力包括:推力在發射筒方向分力、重力分力和摩擦力,扭轉力矩包括:重力力矩、下支點摩擦力矩、研究對象加速造成的質心慣性力矩[3]。該階段數學模型如下:
該階段較為復雜,發射筒滑塊導軌與滑塊的間隙(受加工工藝影響較大)會顯著影響實測結果,多次地面試驗表明,間隙超過某一定值后,仿真結果與實測結果非常吻合。
2.3后滑塊離軌,無控飛行
當導彈后滑塊離軌后,導彈處于無控飛行狀態,且由于發射發動機停止工作,導彈處于減速狀態,因此,忽略該階段氣動力及其產生的力矩。導彈以上階段末的恒定角速度旋轉。該階段數學模型如下:
2.4飛行發動機工作,有控爬升
導彈無控飛行3~5m后,飛行發動機啟動,確保射手安全。控制系統快速啟動,舵機偏轉,由于安裝在發動機噴管處的燃氣舵產生較大的力和力矩,導彈俯仰角快速增大,逐漸爬升至預定高度。該階段數學模型[4]如下:
2.5轉平飛
當導彈爬升至預定高度時,開始低頭轉平飛,該階段攻角為負攻角,飛行時間約為3s,會產生較大的過載。該階段數學模型如下:
式中,?p為轉入平飛時的俯仰角。
2.6平飛
當導彈達到預定高度后,轉入平飛階段,導彈攻角以升力平衡重力方式計算。該階段數學模型如下:
2.7比例導引攻擊
當彈目視線角小于臨界角度后,進入比例導引攻擊階段,臨界彈目視線角qlj、比例系數KP與射手與目標的初始距離r0有關[5]。該階段數學模型為:
3彈道仿真
基于以上數學模型,通過Matlab/simulink軟件建立仿真程序[6],并進行不同狀態下的彈道仿真。彈道設計要求為:彈道傾角大于30°,法向過載小于5g,導引頭框架角小于25°。目標距離小于350 m時,法向過載大于5g。目標距離165 m,相向以20 m/s移動時,彈道傾角僅為12°。其他條件下,制導律滿足設計要求。導彈發射角為18°,目標距離導彈發射處2 000 m,向導彈發射處移動,速度為10 m/s。仿真結果如圖3—圖5所示。
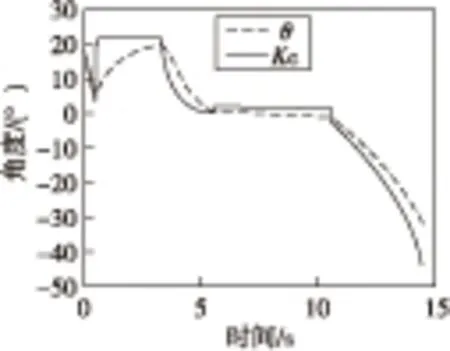
圖3 彈道傾角、俯仰角Fig.3 Inclination angle,Pitch angle
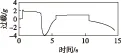
圖4 法向過載Fig.4 Normal overload

圖5 導引頭視線角Fig.5 Sight of seeker
通過以上實驗可以得出,采用燃氣舵風洞試驗和地面發射試驗驗證部分數學模型,試驗結果與仿真結果吻合,表明數學模型準確可靠,可作為頂攻反坦克導彈彈道仿真計算的理論模型。
4結論
本文提出了空氣動力和燃氣動力共同作用下的矢量控制反坦克導彈頂攻彈道模型。該模型包括典型頂攻彈道7個階段的數學模型,各階段模型分別表述了所對應階段的彈道設計方案和力學模型。以這些數學模型為基礎的Matlab/simulink彈道仿真程序進行仿真計算和試驗,結果表明彈道模型能夠滿足彈著角、法向過載、導引頭框架角等要求。為了進一步驗證模型的可靠性和準確性,還需進行質點系彈道仿真。
參考文獻:
[1]任文真,楊姝君,苗昊春.燃氣舵推力矢量控制技術在反坦克導彈上的應用[J].彈箭與制導學報,2013(4):22-24.
[2]候師,張靖,朱湘龍.矢量控制反坦克導彈重力補償設計[J].江南大學學報,2012(8):17-19.
[3]韓子鵬.彈箭外彈道學[M].北京:北京理工大學出版社,2008.
[4]錢杏芳,林瑞雄,趙亞男.導彈飛行力學[M].北京:北京理工大學出版社,2000.
[5]張建偉,黃樹彩,韓朝超.基于Matlab的比例導引彈道仿真分析[J].戰術導彈技術,2009(3):60-64.
[6]喬相信,菅茂生,張健.基于MATLAB的底排彈六自由度彈道仿真[J].彈箭與制導學報,2006(6):173-175.
Top Attack Trajectory Model of Vector Control Anti-tank Missile
LI Yongsheng, LI Jingwei, QUAN Weili, ZHANG Ke
(The 41st Institute of the Sixth Academy ,CASIC, Beijing 010010,China)
Abstract:The vector control research of top attack anti-tank missile are only focused on jet vane control. Aiming at this problem, the aerodynamic model under the joint action of aerodynamics and jet action was put forward in this paper, which proposing mathematical models of 7 stages of typical trajectory for the first time. These models expressed trajectory design proposals and mechanics models of all stages, which were proved to be accurate and reliable by simulation on Simulink, and by wind tunnel test and lauching test as well.
Key words:anti-tank missile; top attack trajectory; vector control
中圖分類號:TJ761.1
文獻標志碼:A
文章編號:1008-1194(2016)02-0064-03
作者簡介:李永盛(1985—),男,甘肅定西人,碩士,研究方向:飛行器設計。E-mail:lysheng850@sina.com。
*收稿日期:2015-10-28

