基于邊際分析法的銀行窗口數量最優化設計
吳希
摘要:文章通過研究銀行排隊現象這樣一個實例,應用排隊理論,對銀行窗口的數量進行定量的優化分析。通過建立排隊模型,結合排隊論的相關知識,利用MATLAB軟件設計了優化窗口數量的科學方法,在保證低成本的情況下使得顧客的滿意程度顯著提高。
關鍵詞:排隊論;邊際分析法;服務成本
隨著社會經濟的不斷發展,銀行間的競爭越來越激烈,怎樣提高銀行服務的質量,滿足儲戶的需求,并控制服務成本是各個銀行急需解決的問題。本文通過分析我市某銀行服務窗口的排隊系統,結合排隊論的有關理論知識,對窗口數量的最優化設計提供了解決的方法,構建了相應的數學模型。
一、排隊論概述
在我們的日常生活中,存在很多的排隊現象,例如乘客排隊等候公共汽車,儲戶在銀行等待服務,學生在食堂等待就餐等等,除了上述“有形”的排隊現象之外,還有大量的“無形”的排隊,排隊的對象不一定是人,也可以是物,例如車站、碼頭等交通樞紐的車船堵塞和疏導問題,通訊衛星與地面若干待傳遞的信息,要降落的飛機因跑道被占用而在空中盤旋等,可以說,排隊現象幾乎是無處不在,無可避免的。為了解決排隊中存在的問題,我們需要對它進行系統的分析。
雖然生活中的排隊問題多種多樣,但是,我們可以將它們抽象為以下的排隊過程(如圖1)。
即顧客從某一顧客源出發,到達服務機構前要求服務,服務機構如果被占用,則需要排隊等待,按照一定的規則接受服務后,離開排隊系統。
綜上,排隊系統主要由三個部分構成,分別是輸入過程,排隊規則和服務機構,下面,分別說明各個分布的特征:
(一)輸入過程:主要描述顧客的來源以及顧客到達排隊系統的規律
顧客源中顧客的數量是有限的還是無限的;顧客到達的方式是單個到達還是成批到達;顧客到達的時間間隔分布是確定型的還是隨機型的(如圖2)。當然如果顧客到達的時間間隔是隨機型的,就需要知道概率分布的類型,分布的參數,分布是否獨立、平穩等。
(二)排隊規則:主要描述顧客排隊等待的隊列和接受服務的次序
顧客排隊等待的隊列可以是有限的,也可以是無限的,隊列的數目可以是單列,也可以是多列。有的排隊問題中顧客可以因為等候時間過長而中途退出,有的則不能退出,必須堅持到接受完服務為止。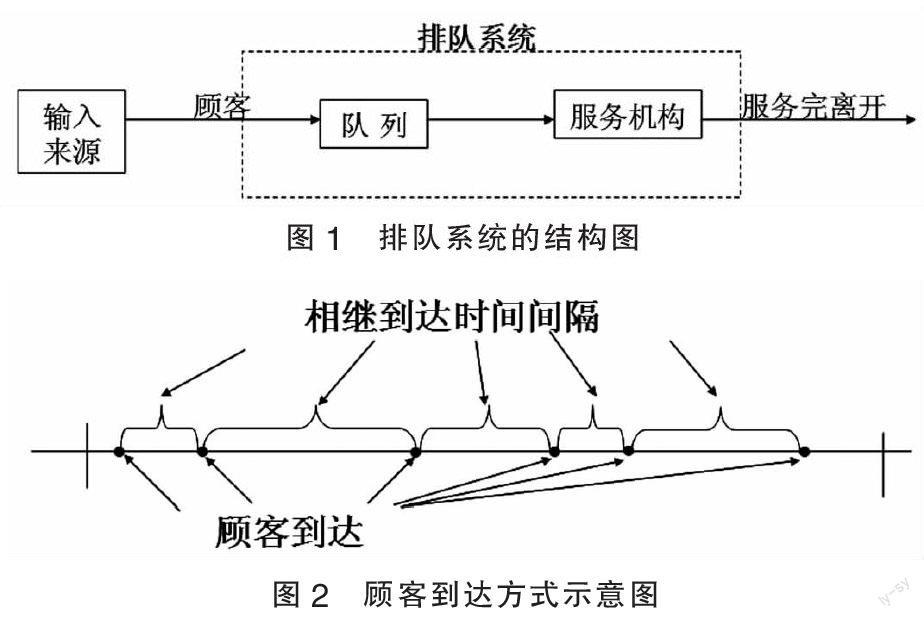
顧客達到時,如果所有的服務機構都被先到的顧客占用,這種情形下若顧客即時自動離開系統,另求服務的稱為損失制;若一直排隊等候,直至接受服務為止的稱為等待制;而將等待制和損失制相結合的服務規則稱為混合制。
對于等待制,顧客接受服務的次序包括:先到先服務,后到先服務,隨機服務和帶優先權的服務。
先到先服務(FCFS)是指按到達的先后次序排成隊伍依次接受服務。當服務設施出現空閑時,排在隊首的顧客優先得到服務,這是排隊問題中最常見的情形。
后到先服務(LCFS)與之恰好相反,指的是最后到達的顧客優先接受服務。
隨機服務(SIRO)指到達服務系統的顧客不形成隊伍,當服務設施有空時,隨機選取一名服務,對每一位等待的顧客來說,被選取的概率是相等的。
帶優先權(PR)的服務是指到達的顧客按重要性進行分類,服務設施優先對重要級別的顧客服務,在級別相同的顧客中按到達的先后順序排隊。
對于混合制,一般允許顧客排隊,但又不允許隊列無限的排下去,可以通過隊長或時間來進行限制。
(三)服務機構:主要描述服務臺的機構形式和工作情況,包括服務臺的數目和排列情況
服務臺的服務方式指對單個顧客進行服務還是成批進行服務,常見的服務方式一般是單個單個地進行服務,但有些特殊的情況,例如公交車對乘客提供的服務就是成批的。
服務時間是確定型的還是隨機型的(如圖3)。當然,一般的服務機構服務時間都是隨機的。對于隨機型的服務時間,分布的類型是什么,參數如何,是否平穩、是否獨立都是需要考慮的問題。
因此,對于銀行窗口服務的排隊問題,可以將其概括為顧客到達滿足Poisson分布,服務時間服從負指數分布,系統容量無限,顧客源無限,采用先到先服務機制的服務機構。
為了研究該服務機構運行的效率、估計服務質量、研究設計改進措施,必須確定一些基本指標,用以判斷系統運行狀況的優劣。
二、銀行排隊系統的特征指標
排隊系統運行情況的的分析,就是在給定輸入和服務條件下,通過求解系統的狀態概率以及運行指標來對排隊現象進行評價和分析。我們選擇吉林市某銀行作為觀察對象,對銀行的服務進行數據的搜集、整理與分析。
對銀行進行實地考查,在不同的時間節點統計單位時間內到達的顧客數量和接受服務的顧客數量。通過半月內的實際統計,計算得到單位時間內顧客到達的數量服從Poisson分布,單位時間內到達的顧客數的數學期望為:
即目前的服務能力無法滿足顧客的需求,除了要提高柜員的服務效率之外,還需要增加一定數量的窗口。
三、窗口數量的最優化設計
通過對數據的分析,我們發現目前銀行的服務基本符合M/M/C排隊模型,因此,基于該模型的基礎上,對窗口數量進行定量化的分析。
利用上述方法,結合MATLAB軟件對銀行網點的數據進行計算,得出邊際分析的結果如表1所示。
從表1中可以看出,就目前的服務率來看,設置4個窗口是比較合適的,此時既能基本滿足客戶的需求,使得顧客逗留的損失達到最低,不會造成嚴重的排隊現象,又能節省一部分成本,使得銀行的服務支出相對最少。
四、總結
本文針對吉林市某銀行的排隊問題,以排隊理論為基礎,結合邊際分析法建立了求解窗口數量的數學模型。模型綜合考慮的銀行的服務成本及顧客由于排隊所導致的逗留損失,與實際緊密結合,具有實際的意義和可操作性。
參考文獻:
[1]胡運權.運籌學教程[M].清華大學出版社,2002.
[2]王興貴,焦爭昌.基于排隊論的銀行排隊問題研究[J].湘潭師范學院學報(社會科學版),2008(01).
(作者單位:吉林醫藥學院)

