基于有限元分析的鋁合金輪轂結構優化設計

（廈門民興工業有限公司，福建 廈門 361006）

【摘 要】輪轂是汽車重要的安全部件。文章對有限元分析軟件進行二次開發，推算并繪制適合A356-T6鋁合金輪轂的零件S-N曲線。運用Simulation軟件，以輪轂徑向沖擊測試為例，建立有限元分析力學模型，分析輪轂沖擊的靜態影響因素和動態沖擊載荷下的最大應力。基于有限元分析，對輪轂進行優化前后強度的分析比較。依據零件S-N曲線，先行預測輪轂強度狀況，從而為鋁合金輪轂的結構設計與優化提供方法和方向。

【關鍵詞】輪轂；二次開發；有限元；S-N曲線；徑向沖擊；優化

【中圖分類號】U463.343 【文獻標識碼】A 【文章編號】1674-0688（2016）07-0059-05

1 概況

隨著社會的發展，汽車已經成為家庭的代步工具，汽車零部件的強度分析對于汽車的安全性能尤為關鍵。汽車輪轂作為汽車重要的安全部件，其強度分析是設計過程中必須考慮的重要因素。隨著汽車市場競爭的加劇，“質量輕、強度高、美觀性強”已經成為現代汽車制造業的主要設計理念，因此在汽車輪轂的初期設計中要體現此設計理念。由于輪轂工作在隨機載荷之下，在其研制中最關心的問題之一就是輪轂的抗徑向沖擊能力，在鋁合金輪轂的設計開發，抗徑向沖擊能力是比較貼近實際行駛路況的測試。因此，如何在設計中優化其結構設計，以減少輪轂開模后在實際試作中的次數和避免強度改善的盲目性，其初期的結構設計和結構優化非常重要。

本文主要闡述如何利用基于Simulation有限元分析軟件來輔助、優化、改善輪轂的結構設計，以尋求到強度高、輕量化的結構設計。首先計算并繪制A356-T6鋁合金輪轂的S-N曲線，并對軟件進行二次開發，然后將S-N曲線寫入軟件材質庫，對鋁合金輪轂進行靜應力分析，再通過S-N曲線，尋找滿足疲勞壽命下所對應的最大應力值。本文主要討論鋁合金輪轂的沖擊應力的有限元力學模型，并與實際生產結果比對，驗證其合理性，以對鋁合金輪轂后續的有限元分析提供方向。

2 輪轂有限元分析及二次開發

2.1 有限元分析及二次開發的意義

目前，國內中小型的鋁合金輪轂企業，設計人員判斷輪轂結構強度主要是基于直覺的準則法，依靠經驗數據的積累和參考類似結構的產品，即產品的開發設計水平主要取決于設計人員的實際經驗和對這些方法的把握能力。設計輪轂結構時，都很少進行結構優化，輪轂的強度全憑經驗設計，強度問題只能在試作過程中測試試驗發現，再根據實際測試結果去改善強度，不僅浪費了生產成本，也拉長了產品的開發周期，延后產品上市時間。

隨著市場的發展和競爭的加劇，客戶對輪轂的可靠性和經濟性要求不斷提高，故需要改進新產品開發流程，提高研發水平和開發設計能力。有限元分析的介入，在產品設計初期就可以對輪轂強度進行仿真，預先發現潛在的問題，并為結構的改善提供了優化方向，增加量產品的可靠性，避免在產品試作過程中的成本和時間的浪費，也可在保證安全可靠的前提下，優化結構，節省不必要的材料，使輪轂達到“高強度、輕量化”的目的。

在有限元分析的基礎上的二次開發技術也很重要，它使有限元分析工作一目了然，操作方便快捷，節省操作環節中不必要的時間浪費。

2.2 S-N曲線的二次開發

以材料標準樣件的疲勞強度為Y軸，以疲勞壽命為X軸，表示一定循環特征下標準樣件的疲勞強度與疲勞壽命之間關系的曲線，成為應力-壽命曲線，也稱S-N曲線。材料的S-N曲線是指把原材料做成圓棒形，在制定的加工精度等級和熱處理工藝下的標準樣件，得到相應的S-N曲線。因此，不同零件、不同形狀、不同加工精度和熱處理工藝，其S-N曲線也自然不同。

Simulation軟件里面只有材料的S-N曲線，利用該曲線對鋁合金輪轂進行有限元分析，模擬的結果會與實際產品的測試結果差距甚遠，對實際生產沒有指導意義。只有計算并繪制出與輪轂實際測試狀況接近的零件S-N曲線，有限元分析才對產品設計有指導意義。目前，鋁合金輪轂主要使用的材料是A356-T6。該材料的一些機械性能及相對比見表1。

σa /σNf+σm /Su=1（1）

公式（1）中，σa為交變應力作用下的平均應力；σNf為完全加載扭力的交變應力；σm為平均應力；Su為強度極限。

根據表1的材料屬性，可以使用公式（1）計算出材料的疲勞壽命。

σ'Nf=σ'f×（2Nf）b（2）

σmax×εa×E=（σ'f）2（2Nf）2b+σ'f ε'f E（2Nf）b+c（3）

σmax=σa+σm

作為鋁合金輪轂，主要材料為AT356-T6。輪轂主要承受靜態疲勞、動態疲勞、瞬間疲勞，使用修正Goodman圖，S-N曲線的修正公式如下：

σa=（Su-σm）×（2Nf）b

σmax=1 822×Nf∧（-0.201）

利用公式，求解出各個節點上的應力值，并繪制出適用于A356-T6為材料的鋁合金輪轂零件的S-N曲線（如圖1所示）。

利用公式，可以直接計算出產品在滿足某個疲勞壽命下的最大應力值。這樣可以大大簡化有限元分析工作，可以不需要模擬在該最大應力下的壽命周期。依照不同的測試標準，對應不同的應力值（見表2）。

很多有限元分析模型以材料的降伏強度來判定沖擊模擬是否成功，其模擬結果與實際沖擊試驗往往差距甚遠，對現實的生產沒有指導意義。而由材料S-N曲線推算修正后的零件S-N曲線對應計算出的應力值作為有限元分析的判定基準，與實際測試比較吻合，可為零件的結構優化和強度改善提供方向。

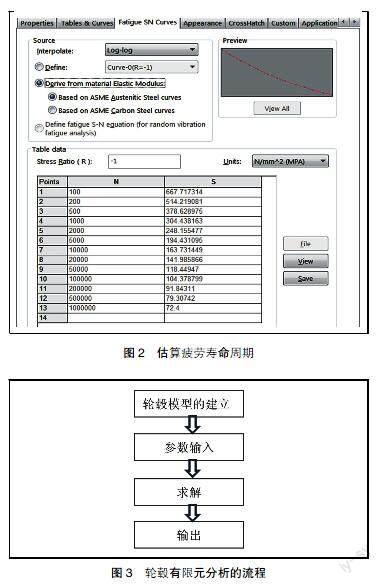
在Simulation有限元分析軟件中寫入每個點對應參數，繪制出相應的S-N曲線，可以較準確地估算疲勞壽命周期（如圖2所示）。

3 基于有限元分析的結構優化

本文主要以22×10.5J+55 5/120MAXLOAD：815 kg為例，以輪轂13度沖擊試驗作為沖擊強度計算，承受瞬間疲勞的有限元模型，來討論基于有限元分析的結構優化。

3.1 輪轂有限元分析的流程

輪轂有限元分析的流程如圖3所示。

3.2 13度沖擊測試有限元模型

13度沖擊試驗是為模擬實際行駛過程中遭遇來自側面撞擊的情況，如石頭或者馬路牙子。輪轂主要承受瞬間疲勞。

沖擊試驗機上有一個從沖擊面至少125 mm寬、375 mm長的垂直動作的重錘。將輪轂裝胎、充氣后，安裝在試驗機上，使輪轂的中心軸線與垂直方向為13°±1°角，其最高點面對重錘。保證重錘在輪轂正上方，并與輪轂重疊25 mm，將重錘提到高于輪轂最上方230 mm處，然后將其釋放，讓沖頭落下沖擊輪轂輪胎總成。

如果試驗中輪輻在任意斷面處有可見性或探傷后大于5 mm裂痕，輪輻從輪輞上分離或者輪胎內空氣在1 min內漏10%以上等現象，就認為試驗失效。如果被重錘面板沖擊的輪截面處出現裂痕但是輪胎沒有漏氣，則不能認為試驗失效。沖擊測試試驗機如圖4所示。

13度沖擊測試有限元分析模型要進行2次分析。分析#1主要是計算沖擊的靜態影響因素。沖擊重錘是從一定高度落下的，因此，還要建立一個分析#2，分析動態沖擊下的最大應力水平。

3.2.1 建立算例

（1）沖擊的主要力量來源為重錘。重錘質量與輪轂的最大載荷有關。

重錘質量的計算公式：

W=0.6×W1+180

公式中，W為重錘質量（kg）；W1為最大荷重（kg）。

W=0.6×815+180=669 kg

（2）模型處理。從輪轂耳部外徑向中心偏移1 inch，切割出輪轂上受重錘沖擊的受力面，一般為2個曲面；再旋轉輪轂，使輪轂的中心軸線與垂直方向為13°，劃分出來的受力面迎接重錘的垂直沖擊。

（3）模型材質賦予。為模型添加材質為A356-T6，其彈性模量為72.4×103 MPa，泊松比為0.33，密度為2.67×103 kg/m3，T6后硬度為75HB，最終成品硬度為90 HB。

（4）設定約束。設定5個P.C.D.螺絲孔為固定，限定X軸轉動、Y軸轉動、Z軸轉動、X軸移動、Y軸移動5個自由度。設定安裝面相對于夾具接觸面的垂直位移為0，限定Z軸移動。這樣就限定了6個自由度，為完全定位。

3.2.2 定義載荷

輪轂沖擊時，要先安裝輪胎，并對輪胎充氣后，安裝在試驗機上，調整好重錘質量和重錘高度，再啟動開關，讓重錘垂直落下，撞擊輪轂。

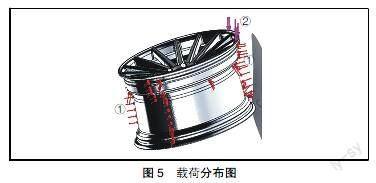
（1）模擬實際沖擊，充氣壓力為29 psi，即輪輞面上受到29 psi的壓力，如圖5的箭頭①所示。

（2）對分割出來的受力面，施加669 kg的重錘質量，如圖5的箭頭②所示。

3.2.3 靜態分析屬性設置

這個步驟對于沖擊分析來說是非常重要的一個步驟。因為分析#1主要是要計算靜態影響因素，即沖擊位置的變形量，所以在“靜態分析屬性設置”里，選擇“大位移”，求解器選擇“自動求解器”（如圖6所示）。

3.2.4 劃分網格

在輪轂的有限元分析工作中，網格劃分的原則是在確保計算精度的前提下，盡量減少網格數量，提高有限元分析的效率。直觀上看，網格各內角或各個邊相差不大、網格面不過分扭曲、邊節點位于邊界等分點附近，這種網格質量較好。

由于輪轂屬旋轉體，故對此輪轂采用基于曲率的網格，經過多次網格劃分和計算，最終確定最大單元格為8 mm，最小單元格為1.6 mm，網格如圖7所示。

3.2.5 有限元模型計算結果分析#1

查看分析結果的最大Iso修剪，可以得出靜態影響因素εs=0.042 inch。即，輪轂受到重錘沖擊后，沖擊位置的最大變形量為0.042 inch（如圖8所示）。

3.2.6 計算沖擊高度影響因素

沖擊試驗有2個重要因素：一是沖擊重錘質量；二是重錘落下高度，即沖擊高度。

沖擊的高度影響因素n的計算公式如下：

n=1+2×（H/εs）^0.5

上式中，n為沖擊高度影響因素；H為沖擊高度（in）；s為靜態影響因素（in）。

計算出n=1+2×{（230/25.4）/0.042}^0.5=22.18。

3.2.7 計算動態沖擊載荷Li

動態沖擊載荷，即模擬重錘由一定高度落下，砸到輪轂上，對輪轂施加的載荷。

動態沖擊載荷Li的計算公式如下：

Li=W×n×Af

上式中，W為重錘質量；n為沖擊高度影響因素；Af為吸收因素，是一個因輪胎、安裝夾具等減少沖擊力的一個經驗常數，取0.152。

計算得出：Li=669×22.18×0.152=2 256 kg。

3.2.8 有限元模型計算結果分析#2

返回“定義載荷”模型，將載荷修正為2 256 kg，計算沖擊應力。經有限元分析模型，分析得出其應力值，最大應力的位置及大小如圖9所示：最大應力274.1 MPa>沖擊極限應力230 MPa，判定為沖擊不合格。而此款輪轂的實際測試不合格照片如圖10所示，也是在輪輞與耳部交接處撕裂，與模擬結果相符。

3.3 結構優化方案

針對輪輞與窗口交接處應力大，判定為此處強度較弱，優化方案如下：將耳部厚度由6 mm增厚到7.5 mm，并將輪輻與耳部交接處R角由R2改大至R4。優化前后3D造型對比如圖11、圖12所示。

（1）重新進行有限元模型分析，分析結果#1，得出靜態影響因素：εs=0.081 9。

（2）計算出沖擊的高度影響因素：n=1+2×{（230/

25.4）/0.0819}^0.5=15.86。

（3）計算動態沖擊載荷：Li=669×15.86×0.152=

1 613 kg。

（4）返回“定義載荷”模型，將載荷修正為1 613 kg，得出分析結果#2。經有限元分析模型，分析得出其應力值，最大應力的位置及大小如圖13所示。

最大應力200.7 MPa<沖擊極限應力230 MPa，判定為沖擊合格。

實際生產中，依此方案修改，其測試結果（如圖14所示）也較佳。

4 結語

本文以A356-T6鋁合金輪轂為研究對象，推算適合鋁合金輪轂零件的S-N曲線，并以有限元分析軟件為輔助工具，盡力輪轂力學模型，對輪轂進行沖徑向沖擊應力有限元結構強度分析，找到輪轂強度的改善方向和優化輪轂結構思路，以減少輪轂開模后試做的次數和避免強度改善的盲目性，使新產品實際的開發過程節約更多的時間與成本，增強企業的競爭力，為客戶的新品上市贏得時間。

參 考 文 獻

[1]Mehadad Zoroufi & Ali FAtemi.Fatigue Life Compar-isons of Competing Manufacturing Processes：A Study of Steering Knuckle[J].The University of Toledo，2004（1）.

[2]酈明.汽車結構抗疲勞設計[M].合肥：中國科學技術大學出版社，1995.

[3]徐灝.疲勞強度設計[M].北京：機械工業出版社1981.

[4]程育仁，繆龍秀，侯炳麟.疲勞強度[M].北京：中國鐵道出版社，1990.

[5]王渭新，張磊，劉智沖.有限元分析在輪轂設計中的應用[J].現代制造技術與裝備，2007（4）.

[6]李平化，周華祥，龍華.鋁車輪設計的有限元分析[J].裝備制造技術，2006（6）.

[責任編輯：鐘聲賢]

【作者簡介】劉銀峰，男，福建安溪人，本科，廈門民興工業有限公司工程師，研究方向：鋁合金輪轂有限元模型。