基于復合多尺度模糊熵的滾動軸承故障診斷方法

鄭近德, 潘海洋, 程軍圣, 張　俊 (.安徽工業大學 機械工程學院，安徽 馬鞍山　4303; .湖南大學 汽車車身先進設計制造國家重點實驗室，長沙　4008)

?

基于復合多尺度模糊熵的滾動軸承故障診斷方法

鄭近德1, 潘海洋1, 程軍圣2, 張俊1(1.安徽工業大學 機械工程學院，安徽 馬鞍山243032; 2.湖南大學 汽車車身先進設計制造國家重點實驗室，長沙410082)

摘要：為了精確地提取滾動軸承振動信號非線性故障特征，針對多尺度熵(Multi-Scale Entropy，MSE)中粗粒化方式的不足，提出一種新的衡量時間序列自相似性和復雜性的方法——復合多尺度模糊熵(Composite Multi-Scale Fuzzy Entropy，CMFE)。與MSE相比，CMFE綜合同一尺度下多個粗粒化序列的信息，隨著尺度因子的增加，熵值變化更加穩定，一致性更好。在此基礎上，結合Fisher得分特征選擇和支持向量機模式分類，提出了一種新的滾動軸承智能故障診斷方法。將提出的方法應用于滾動軸承實驗數據分析，通過對比結果驗證了所提出方法的有效性和優越性。

關鍵詞：多尺度熵；復合多尺度模糊熵；特征選擇；滾動軸承；故障診斷

當機械設備出現故障時，振動信號往往表現出非線性和非平穩特征。因此，許多非線性動力學的方法由于能夠有效地提取隱藏在振動信號中其它線性方法無法提取的故障特征信息而在機械故障診斷中得到了廣泛的應用[1]。如近似熵，樣本熵和多尺度熵等已被應用于機械故障診斷領域。Yan等[1]將近似熵應用于機械系統健康狀態監測；趙志宏等[2]將樣本熵應用于滾動軸承的故障診斷，提出了一種基于集成經驗模態分解和樣本熵的故障診斷方法；鄭近德等[3-5]將多尺度熵應用于滾動軸承和轉子系統的故障診斷。

多尺度熵(Multi-Scale Entropy, MSE)是Costa等[6-7]針對單一尺度的熵值不能有效衡量時間的復雜性而提出的，MSE通過粗粒化的方式實現對時間序列進行多尺度化，從而實現對時間序列的多尺度分析。MSE能夠有效地衡量時間序列不同尺度因子的復雜性，因而能更好地反映時間序列隱藏在不同尺度的模式信息。但是，不足的是，MSE主要存在如下兩個缺陷：① MSE中樣本熵(Sample Entropy，SampEn)的計算相似性度量函數由于采用的是階躍函數，因此在度量相似性時會發生突變[8-9]；② 在MSE粗粒化序列的計算中，基于粗粒化定義的多尺度計算方法對時間序列的長度依賴性較大。由于每個粗粒化序列的長度等于原信號的長度除以尺度因子，熵值的偏差會隨著粗粒化序列長度減小而增大，而且多尺度序列熵值的估計誤差也會隨著尺度因子的增大而增大[10]。

為了克服MSE存在的上述缺陷，論文提出了如下的改進方法。針對問題①采用模糊熵[9](Fuzzy Entropy，FuzzyEn)代替樣本熵，FuzzyEn采用指數函數代替單位階躍函數，克服了相似性度量的突變；針對問題②采用復合多尺度的方法以克服傳統粗粒化方式存在的不足。由此提出了一種新的衡量時間序列復雜性的方法——復合多尺度模糊熵(Composite Multi-Scale Fuzzy Entropy，CMFE)。CMFE綜合了同一尺度下多個粗粒化序列的信息，很好地抑制了由于時間序列變短而導致熵值突變，得到的CMFE曲線穩定性和一致性更好。

由于機械系統運行的復雜性，其振動信號包含的與故障有關的信息往往分布在不同的尺度，因此，對振動信號進行多尺度分析是一種有效的故障特征提取方法。當滾動軸承發生故障時，振動信號的復雜性會發生改變；對于不同的故障類型和故障程度，引起的摩擦和沖擊的頻率不同，相應地振動信號的復雜性也會不同。因此，CMFE能夠及時和準確地檢測振動信號的復雜性變化。基于此，論文將CMFE應用于滾動軸承振動信號復雜性的量度，提取隱藏在振動信號不同尺度的深層故障信息。此外，由于包含所有尺度因子特征不可避免地會有信息冗余，為了降低特征維數，提高故障診斷的效率，將Fisher 得分(Fisher Score，FS)應用于滾動軸承敏感故障特征的提取[11]。同時，為了實現滾動軸承故障的智能診斷，將訓練速度快、適合小樣本分類廣泛應用于機械故障診斷領域的分類方法——支持向量機(Support Vector Machine，SVM)應用于滾動軸承故障的智能分類[12-13]。在此基礎上，提出了一種基于CMFE，FS和SVM的滾動軸承的故障診斷方法。實驗數據分析表明，論文提出的方法能夠有效地提取機械故障特征，具有較高的故障識別度。

1復合多尺度模糊熵

1.1多尺度熵

多尺度熵(MSE)定義為不同尺度的樣本熵，從不同的尺度衡量時間序列的復雜性，克服了傳統的基于單一尺度的樣本熵衡量時間序列復雜性的缺陷，能夠反映時間序列更深層的模式信息。MSE的計算步驟簡述如下[6-9]：

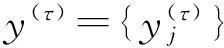
(1)

式中，τ為正整數，稱為尺度因子。τ=1時，粗粒化序列即為原時間序列；τ>1時原始序列被粗粒化成長度為[N/τ](表示不大于N/τ的最大正整數)的粗粒化序列；

(2) 計算每個尺度因子下粗粒化序列的樣本熵，即

MSE(X,τ,m,n,r)=SampEn(y(τ),m,n,r)

(2)

并將MSE表示成尺度因子的函數，稱為多尺度熵分析。

MSE克服了傳統的基于單一尺度樣本熵衡量時間序列不易得到準確結論的不足，但是，在MSE的計算中，基于粗粒化方式定義的多尺度算法依賴于時間序列的長度，每個粗粒化序列的長度等于原時間序列的長度除以尺度因子，熵值的偏差會隨著粗粒化序列長度減小而增大。以尺度因子τ為2和3為例，圖1給出了粗粒化過程的算法示意圖。

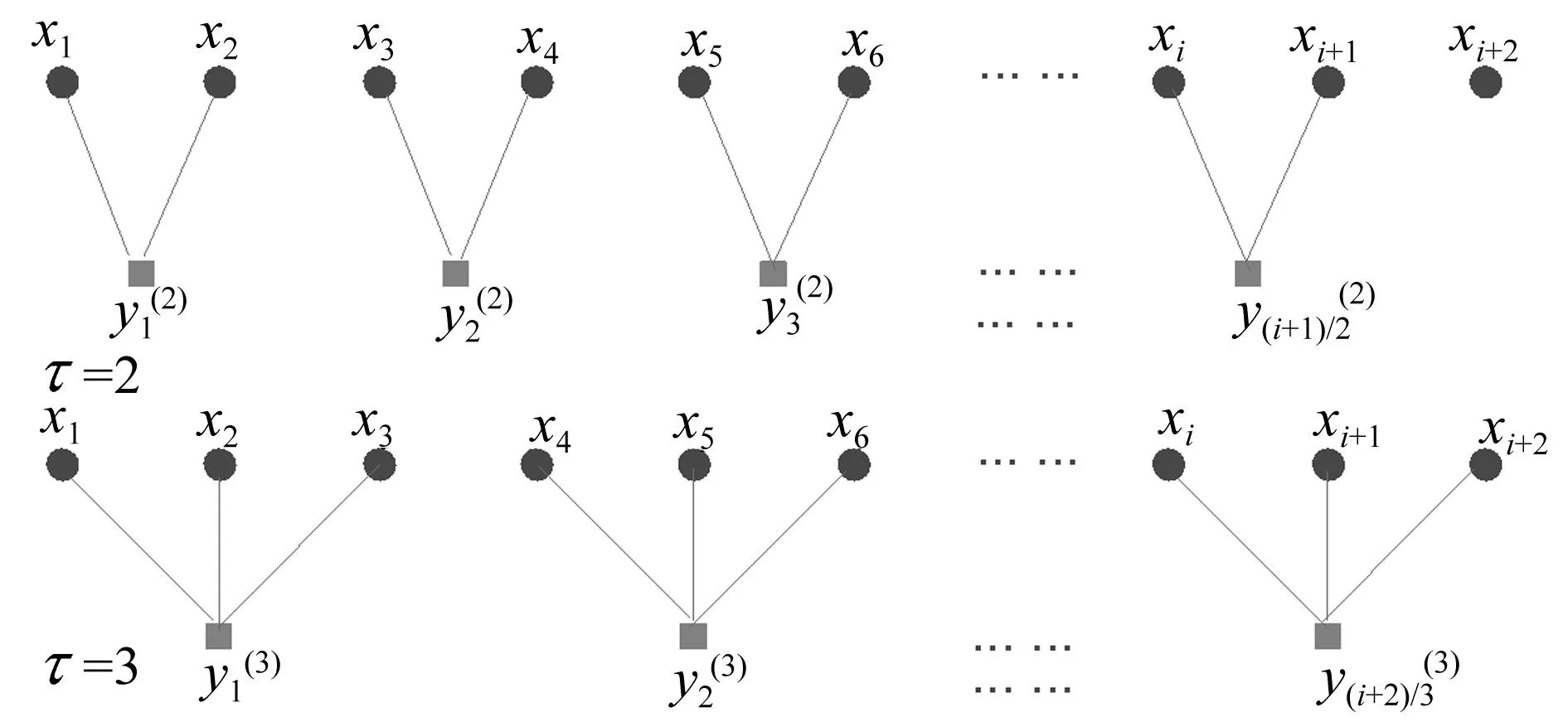
圖1　尺度因子等于2和3時的多尺度化方法Fig.1 The multi-scale way with scale factor equaling to 2 and 3

從圖1中可以看出，當尺度因子τ等于2時，粗粒化后的序列依次序兩兩平均，只考慮了x(1)與x(2)求均值開頭的粗粒序列，而未考慮x(2)與x(3)求均值作為開頭的序列，此序列相對于原始序列的尺度因子同樣是2；同樣地，對于尺度因子等于3時，只考慮了x(1)，x(2)和x(3)求均值開頭的粗粒序列，而未考慮x(2),x(3)與x(4)求均值以及x(3),x(4)與x(5)求均值開頭的兩個粗粒序列，此兩序列相對于原始序列的尺度因子也同樣是3。

1.2復合多尺度模糊熵

為了克服MSE存在的缺陷，論文提出了復合多尺度模糊熵(CMFE)算法。CMFE算法中，首先采用FuzzyEn代替樣本熵，克服了相似性度量的突變；其次，針對粗粒化過程中由于時間序列變短而對模糊熵計算帶來的影響，采用相同尺度因子下的不同粗粒化序列的模糊熵的均值作為該尺度因子下的模糊熵值。CMFE具體計算步驟如下：

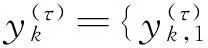
(3)

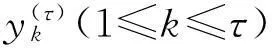
CMFE(X,τ,m,n,r)=

(4)

CMFE綜合了同一尺度下所有粗粒化序列的模糊熵信息，因此，結果比MSE更合理，以尺度因子等于2為例，復合多尺度的計算方法如圖2所示。

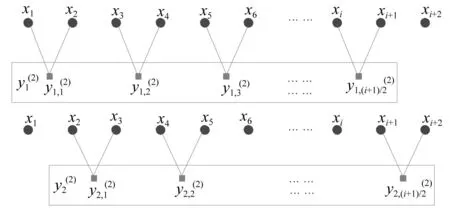
圖2　尺度因子等于2時的復合多尺度方法Fig.2 The composite multi-scale way with scale factor equaling to 2

與MSE類似，CMFE曲線反映了時間序列在不同尺度因子下的復雜性。如果一個時間序列的熵值在大部分尺度上都比另一個時間序列的熵值大，那么就認為前者比后者更為復雜；如果一個時間序列隨著尺度因子遞增而熵值單調遞減，那么這就意味此序列結構相對較簡單，只在較小的尺度因上包含較多的模式信息。

2CMFE與MSE對比分析

2.1參數的選擇

CMFE計算不僅與數據長度N有關，還與嵌入維數m，相似容限r以及指數函數梯度參數n有關。① 嵌入維數m。一般取嵌入維數m=2，在序列的聯合概率進行動態重構時，m越大包含越多的詳細信息，但m越大需要的數據長度就越長(N1=10m～30m)，因此，綜合考慮，m=2。② 相似容限r。r表示比較窗口邊界的

寬度，控制模板匹配的相似性，r過大會導致模板匹配較難而會丟失掉很多統計信息，r過小，估計出的統計特性效果不理想，且導致結果對噪聲的敏感性增加。一般r取0.1～0.25SD(SD是原始數據的標準差)，本文取r=0.15SD。③n決定相似容限邊界的梯度，在模板相似性的計算中起著權重的作用。n越大梯度越大，n過大導致細節信息丟失，特別地，趨于無窮大時指數函數退化為單位階躍函數，此時邊緣的細節信息被全部遺棄。因此，為了捕獲盡量多的細節信息，一般取較小的整數，n=2。④ 數據長度τ。數據長度對計算結果的影響較小，對于樣本熵和模糊熵，若取m=2，則一般地時間序列長度N1=100～900，因此，計算CMFE時，N≥100τmax，τmax為最大尺度因子。

2.2CMFE與MSE仿真分析

為了將CMFE與MSE進行對比，分別對不同長度的高斯白噪聲信號和1/f噪聲信號進行分析，二者的時域波形和頻譜如圖3所示。

分別采用MSE和CMFE對長度N=2 048, 4 096, 6 192, 8 192和10 240的白噪聲與1/f噪聲進行分析，結果如圖4所示，其中m=2,n=2，r=0.15SD。由圖4可以看出，首先，隨著尺度因子的增加，白噪聲的MSE和CMFE曲線逐漸減小，1/f噪聲的MSE和CMFE變化平穩趨于常數，但是二者的MSE曲線隨著尺度因子增大而波動較大，而CMFE曲線隨著尺度的增大而變化平緩，這說明隨著尺度因子的增加CMFE比MSE得到穩定值的一致性更好。其次，當數據長度N大于2 048時，兩個信號不同長度的數據的CMFE或MSE曲線相差很小，這說明數據長度對MSE和CMFE的計算影響較小；再次，白噪聲CMFE(或MSE)曲線隨著尺度因子增大而減小，這說明白噪聲信號所包含的信息較少，結構較簡單；而1/f噪聲的CMFE(或MSE)隨著尺度因子的變化而趨于平穩，且在大部分尺度上1/f噪聲的熵值大于白噪聲的熵值，這說明1/f噪聲包含的信息比白噪聲信號要復雜的多[6-7]。

圖3　高斯白噪聲與1/f噪聲的波形和頻譜Fig.3 Waveforms and spectra of Gaussian white noise and 1/f noise

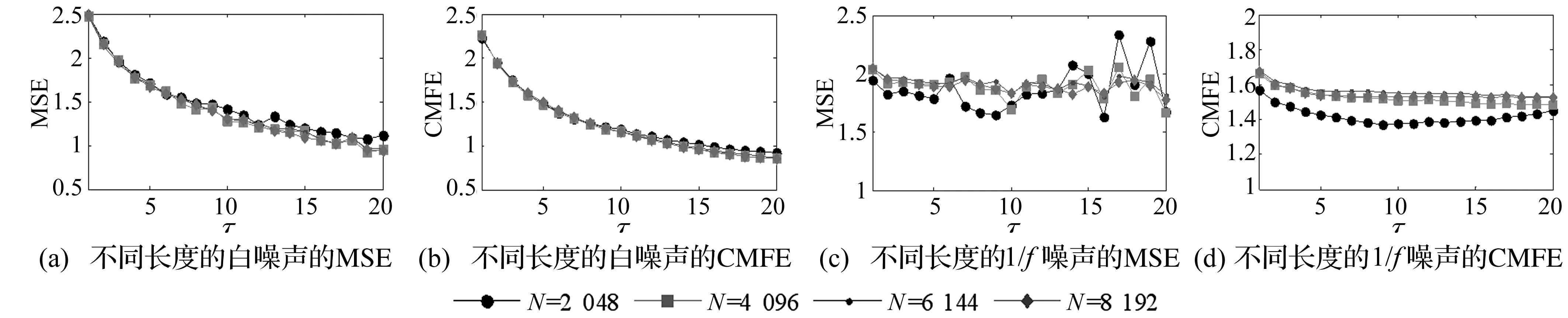
圖4　不同長度的高斯白噪聲和1/f噪聲的MSE和CMFE曲線Fig.4 MSE and CMFE of Gaussian white noise and 1/f noise with different lengths

為了研究參數相似容限r對CMFE結果的影響，考慮r取值0.05SD, 0.1SD, 0.15SD, 0.2SD和0.25SD(SD為原始數據的標準差)時白噪聲與1/f噪聲的MSE和CMFE，結果如圖5所示。由圖5可以看出，對不同的r，白噪聲和1/f噪聲的MSE在較大的尺度因子處都出現了較大的波動，而CMFE曲線變化平緩，一致性更好；隨著r的增大，雖然同一尺度因子下的CMFE和MSE的熵值逐漸降低，但白噪聲和1/f噪聲的MSE或CMFE的變化趨勢與r無關。當相似容限r較大時，會有較少的模板信息記入匹配，熵值較小，會遺漏很多重要信息；而當相似容限較小時，會有太多的模板記入匹配，熵值對野點和噪聲信息的敏感性增強(如圖中r=0.05時MSE波動最大)，綜合考慮，r=0.15SD。

圖5　不同相似容限r下白噪聲和的1/f噪聲的MSE和CMFEFig.5 MSE and CMFE of 1/f noise with different similar tolerance r

3故障診斷方法

上述分析表明，CMFE是一種有效的時間序列的復雜性分析方法，不僅能夠從多個尺度反映序列的復雜性特征，具有計算所需數據短和魯棒性好等優點。

由于機械系統的復雜性，其振動信號的包含的與故障有關的信息往往分布在不同的尺度。正常滾動軸承的振動信號是復雜的隨機振動，當滾動軸承發生故障時，振動出現規律和周期性的摩擦或沖擊，這導致機械系統振動的確定性增加、隨機性降低。對于不同的故障類型和故障程度，引起的摩擦和沖擊的頻率和幅度不同，相應地振動信號的復雜性也不同。因此，CMFE非常適合處理振動信號。

但是，并非所有尺度的CMFE值都與故障信息密切相關，熵值中也包含了過多冗余信息，影響故障診斷的效率。Fisher 得分(FS)[11]是在應用較為廣泛的特征選擇算法之一，算法的目標是從原始的特征中確定最能夠表示各特征之間差別的子集。FS通過對每一個特征計算一個得分，再依據得分從所有特征中選擇期望得到數目的特征子集。事實上，FS是通過估計每個特征向量對不同類屬性的區分能力，從而得出所有特征的排序。特征子集最大程度上確定了各個類別之間的差別，能夠表征原始特征集的本質特征。因此，論文將FS應用于滾動軸承敏感故障特征的選擇，從所有特征中選擇與故障最密切相關的特征子集。同時，為了實現滾動軸承故障的智能診斷，降低診斷結果對人為經驗知識的依賴，將訓練較快、適合小樣本分類的支持向量機(SVM)應用于滾動軸承故障的模式識別，SVM的詳細介紹參見文獻[12-13]。

3.1故障診斷方法

基于CMFE，FS和SVM的滾動軸承故障診斷方法，具體步驟如下：

(1) 假設滾動軸承的運行狀態包含K種類型，每一類的樣本數目分別為M1，M2,…,MK；計算每一類振動信號的CMFE，得到K個特征集：(Tk,k), 其中，Tk∈RMk×τmax，τmax是最大尺度因子也是特征值數目，k=1, 2, …,K；

(2) 采用FS對特征集的τmax個特征值依照得分的高低進行排序，將得分較高的前q個特征作為原始特征集的敏感故障特征子集；

(4) 將訓練樣本輸入到基于SVM的K類故障分類器，對其進行訓練。其中，基于SVM的K類故障分類器中，采用偏二叉樹的思想建立多故障分類器，以K=4為例，多分類器的建立如圖6所示，圖中數字表示類別；

(5) 采用測試樣本對多故障分類器進行測試，依據輸出結果判斷滾動軸承的運行狀態。

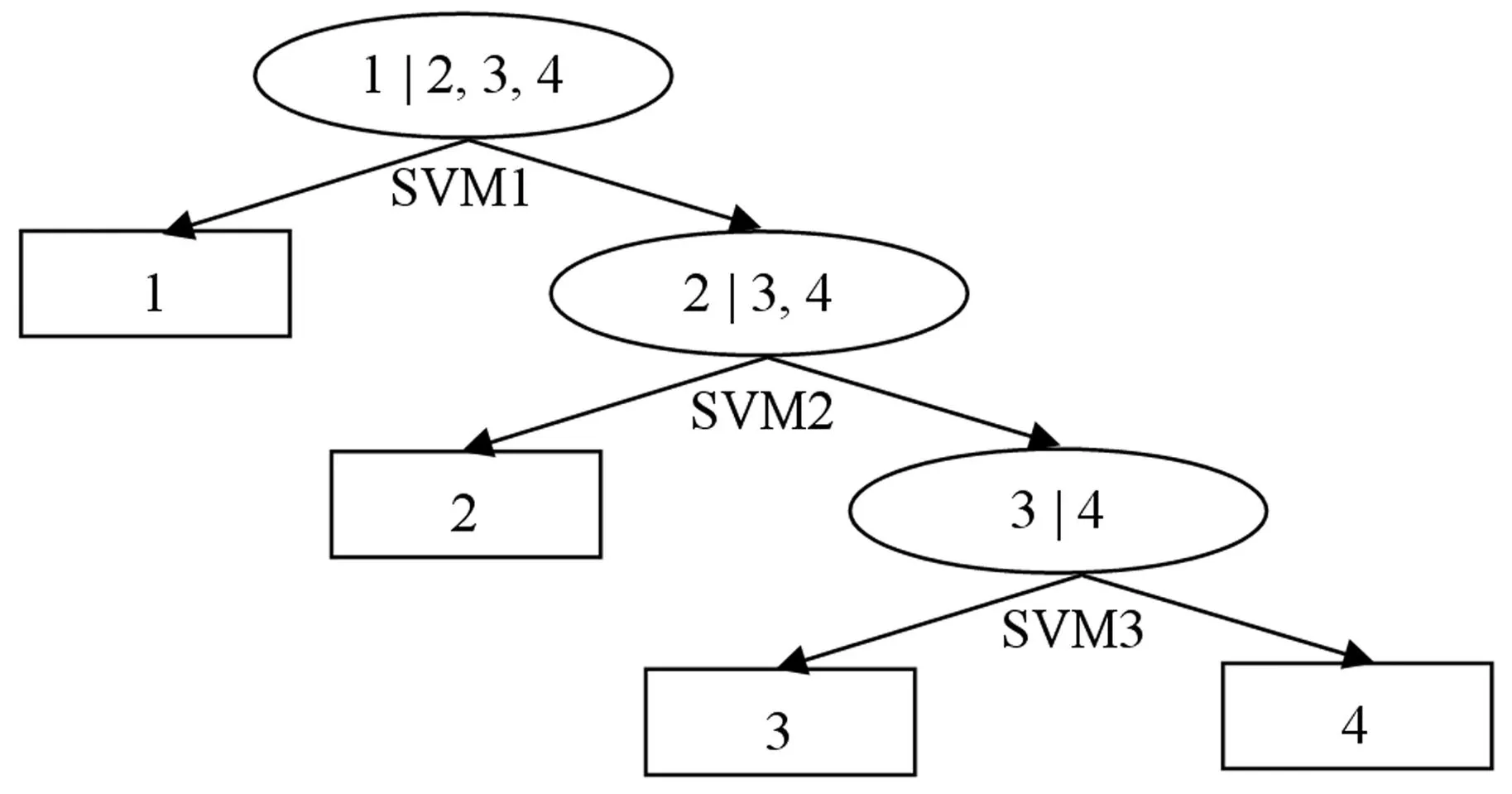
圖6　基于SVM的多故障分類器示意圖Fig.6 Schematic diagram of SVM based multi-fault classifier

為了驗證提出的方法的有效性，將其應用于試驗數據分析。試驗數據采用美國Case Western Reserve University的滾動軸承試驗數據。測試軸承為6205-2RSJEM SKF深溝球軸承，使用電火花加工技術在軸承上布置單點故障，故障直徑分別為：0.017 78 mm, 0.035 56 mm, 0.0.533 4 mm三種大小，故障深度為0.279 4 mm，轉速分別為1 797 r/min，1 772 r/min，1 750 r/min，1 730 r/min，采樣頻率為12 kHz，采集到具有局部單點電蝕的內圈(Inner Race, IR)、外圈(Outer Race,OR)、滾動體故障(Ball Element, BE)和正常(Norm)四種狀態的振動信號，每種狀態取3組數據，每個數據長度為4 096。

為了驗證CMFE方法能夠應用于滾動軸承故障特征提取，考慮如下的兩個試驗。

試驗1:考慮轉速1 797 r/min、負載0 HP，轉速1 772 r/min、負載1 HP，轉速1 750 r/min、負載2 HP和轉速1 730 r/min、負載3 HP四種條件，采集到的正常滾動軸承的振動信號，依次分別記為：Norm1，Norm2，Norm3和Norm4；同時考慮在轉速1 730 r/min、負載3 HP條件下，故障大小分別為0.017 78 mm, 0.035 56 mm, 0.0.533 4 mm的內圈故障滾動軸承的振動信號，分別記為IR1，IR2和IR3，它們的波形如圖7所示。

由圖7可以看出，四種正常滾動軸承的振動信號波形無明顯區別，三種具有內圈故障滾動軸承的振動信號也無明顯區別，雖然隨著故障程度的增加，沖擊特征較明顯，但故障程度仍然不易辨別。采用CMFE分析上述四種狀態的正常滾動軸承的振動信號和三種不同故障程度的內圈故障的滾動軸承的振動信號，每種狀態采用三個樣本，結果如圖8所示。

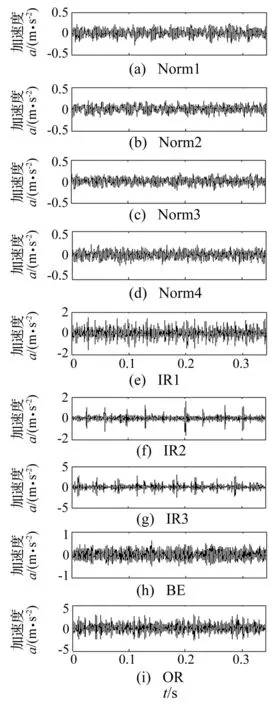
圖7　滾動軸承振動信號的時域波形Fig.7 Time domain waveform of rolling bearing vibration signals

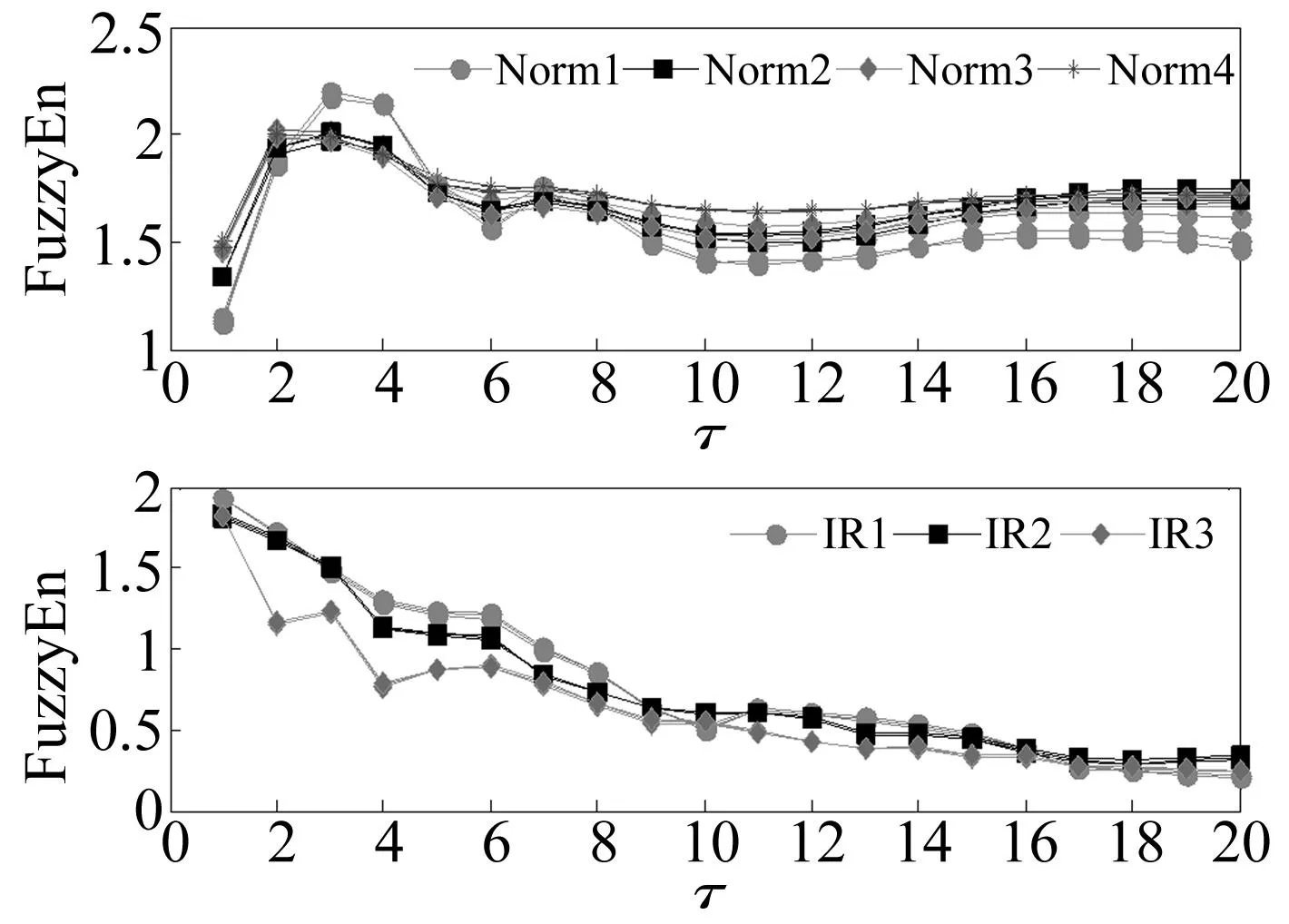
圖8　不同狀態正常軸承振動信號和不同程度內圈故障軸承振動信號的CMFE曲線Fig.8 CMFEs of normal bearing vibration signal under different states, and CMFEs of vibration signals from bearing with inner race fault in different degrees

首先，由圖8可以看出，對于不同轉速和負載的正常滾動軸承信號的CMFE曲線的變化趨勢基本是一致的。這說明轉速和負載對CMFE曲線的變化影響較小，對工況條件具有很好的魯棒性。其次，圖8中具有內圈故障振動信號的CMFE曲線是單調遞減的，這是因為當出現內圈故障時，滾動軸承的振動出現周期性的沖擊，振動信號的自相似性增加，熵值降低。再次，隨著故障程度的加重，熵值遞減的速度越快，即相同尺度的熵值降低。這可以解釋為，故障程度越重，沖擊特征越明顯，振動信號的自相似性也更強，因此，熵值也越小。綜上，試驗1說明，CMFE能夠區分正常和故障以及故障程度敏感，對工況條件如轉速和負載等有較好的魯棒性。

試驗2:再考慮相同工況條件下不同故障類型的實驗數據。考慮轉速1 730 r/min、負載3 HP條件下正常以及故障大小為0.177 8 mm的外圈，內圈和滾動體故障的滾動軸承振動信號。四種狀態滾動軸承振動信號波形如圖7所示，其中四種狀態的信號分別為：Norm4，IR1, BE和OR。

采用CMFE對上述每種狀態的三組數據進行分析，結果如圖9所示，從圖中可以看出，首先，在大部分尺度上，正常軸承的振動信號模糊熵值較大，且隨著尺度因子的增大變化平緩；而三種具有故障的滾動軸承的振動信號的CMFE曲線出現明顯的逐漸遞減趨勢。這是因為當軸承在正常情況下工作時，振動雖然是隨機振動，但這種隨機性不同于白噪聲而類似1/f噪聲(從變化趨勢可以看出)，仍包含了重要的系統信息。當軸承發生故障時，故障部位會成為一個激勵源不斷持續地產生沖擊，因此，得到的振動信號具有明顯的規律性和自相似性，最明顯的是，包含以故障特征頻率為間隔的沖擊成分，導致相應的自相似性程度增加，復雜性程度降低，熵值降低。

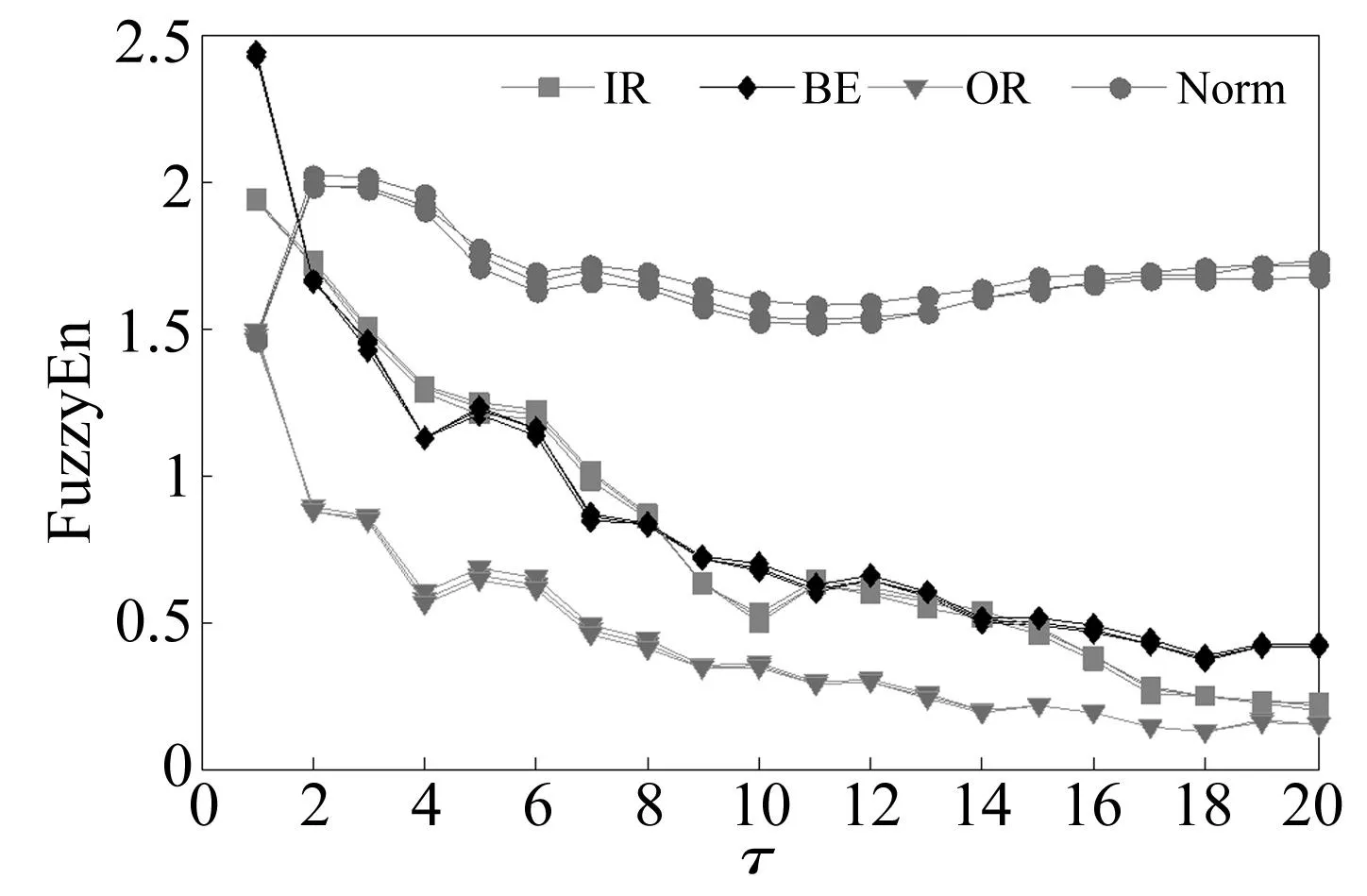
圖9　四種狀態滾動軸承振動信號的CMFEFig.9 CMFEs of rolling bearing vibration signal of the four states

其次，在大部分尺度上，滾動體故障滾動軸承振動信號的CMFE大于內圈故障滾動軸承振動信號的CMFE，大于外圈故障滾動軸承振動信號的CMFE。當發生故障時，系統振動信號具有明顯的沖擊特征，但不同位置的故障，沖擊頻率不同，因此，信號的復雜性程度也不同。由于外圈是固定的，當外圈發生故障時，沖擊特征頻率單一，與內圈故障和滾動體相比，故障特征頻率最小，自相似性和規律性最強，因此，隨著尺度因子的增加，下降速度最快。而內圈隨軸一起轉動，滾動體不僅要隨軸轉動，還要自轉，而且滾動體故障的特征頻率最大。因此，理論上滾動體故障要比內圈故障更為復雜，這可以解釋滾動體故障振動信號的CMFE在大部分尺度上要大于內圈故障和外圈故障振動信號CMFE的原因。

再次，單一尺度上的CMFE并不能有效地區分故障。當尺度因子等于1時，CMFE即是原始振動信號的模糊熵，從圖中可以看出，正常滾動軸承振動信號的熵值較小，小于三種故障滾動軸承振動信號的模糊熵，很容易得出正常滾動軸承復雜性程度低、自相似性程度高，比故障滾動軸承復雜的錯誤觀點，而且不具有物理意義。因此，與傳統的基于單一尺度的樣本熵相比，CMFE跟能夠更好更全面地反映故障信息，這也說明了進行多尺度分析的必要性和優越性。

由上分析也可以發現，盡管CMFE對負載和轉速等工況條件不敏感，但是，僅僅從CMFE曲線無法直接確定故障類別和故障程度，而且診斷結果過多地依賴經驗知識的分析。為了提高故障診斷的效率，論文提出了基于CMFE，FS和SVM的滾動軸承故障診斷新方法。

3.2實驗數據分析

對上述實驗數據，考慮在轉速1 730 r/min、負載3 HP的條件下，正常(Norm4)及點蝕大小為0.177 8 mm的外圈(OR)和滾動體(BE)故障的滾動軸承振動信號。同時考慮轉速1 730 r/min、負載3 HP條件下故障大小分別為0.017 78 mm, 0.035 56 mm, 0.0.533 4 mm的內圈故障滾動軸承的振動信號(IR1，IR2，IR3)。將滾動軸承上述六種狀態的振動信號：Norm4，BE，OR，IR1，IR2，IR3依次標記為1～6類。

將提出的方法應用于實驗數據，具體步驟如下：

步驟1每種狀態取21個樣本，共得到126個樣本；計算每一類樣本的CMFE，得到它們的特征集(Tk,k), 其中，Tk∈RMk×τmax，τmax=20，Mk=20，k=1, 2, …, 6；

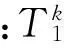
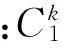
由表1可以看出，論文提出的方法對測試樣本的識別率達到100%，所有的測試樣本都得到了正確分類，這說明了論文方法的有效性。

為了對比，不失一般性，分別考慮特征向量為單一尺度模糊熵和隨機選擇五個尺度的CMFE的情形。單一尺度的模糊熵選擇尺度因子等于1時，隨機選擇的五個尺度的CMFE為：1, 7, 10, 15和19。在與上述相同參數下分別對基于SVM的多故障分類器進行訓練和測試。其中，采用單一尺度的模糊熵對所有特征進行訓練和測試時，輸出樣本分類錯誤率較高，結果不理想，不再列出。再隨機采用五個尺度的CMFE作為特征子集對基于SVM的多故障分類器進行訓練和測試時，結果如表2所示，其中，測試樣本的第五類內圈故障2的一個樣本被錯分為第六類內圈故障3中，故障識別率為97.6%。因此，上述對比表明，單一尺度的熵值并不能完全反應故障的本質特征，這說明進行多尺度分析的必要性；同時，隨機選擇的五個尺度的CMFE作為特征向量進行訓練和測試的識別率比論文提出的方法識別率要低，這說明了論文方法中進行FS特征選擇的必要性。

最后，為了將CMFE與MSE對比，從原始信號中提取滾動軸承的MSE，在與論文方法相同的參數條件下，隨機選擇2, 6, 9, 14和18五個尺度的MSE作為特征進行訓練和測試，在與上述相同參數下對基于SVM的多故障分類器進行訓練(為節約篇幅，詳細結果不再給出)，有兩個測試樣本被錯分，故障識別率約為95.2%。綜上所述，以上對比分析結果表明了論文方法的有效性和優越性。

表1　論文方法測試樣本的診斷結果

表2　隨機選擇特征時測試樣本的診斷結果

4結論

(1) 提出了一種衡量時間序列復雜性的新方法——復合多尺度模糊熵(CMFE)。通過仿真信號將其與多尺度熵進行了對比分析，結果表明CMFE得到穩定值的一致性更好。

(2) 將CMFE應用于滾動軸承試驗數據分析，結果表明，CMFE能夠有效地區分滾動軸承的故障程度和故障類型。

(3) 提出了一種基于CMFE、Fisher得分和支持向量機的滾動軸承故障診斷方法，通過實驗數據分析將其與現有方法進行了對比，結果表明了論文方法的有效性和優越性。

總之，論文在提出了一種新的非線性動力學方法——復合多尺度模糊熵的基礎上，提出了一種新的滾動軸承故障診斷方法，試驗數據分析結果驗證了方法的有效性。盡管如此，方法也有不足之處，如CMFE參數的選擇需要人為設定，作者下一步將對多尺度熵理論進行完善，以期能夠將其應用于機械運行狀態的實時監測和早期故障的預警。

參 考 文 獻

[ 1 ] Yan Ru-qiang, Gao R X.Approximate entropy as a diagnostic tool for machine health monitoring [J].Mechanical Systems and Signal Processing, 2007, 21 (2): 824-839.

[ 2 ] 趙志宏，楊紹普.一種基于樣本熵的軸承故障診斷方法[J].振動與沖擊，2012, 31(6): 136-140.

ZHAO Zhi-hong, YANG Shao-pu.Sample entropy-based roller bearing fault diagnosis method[J].Journal of Vibration and Shock, 2012, 31(6): 136-140.

[ 3 ] 鄭近德, 程軍圣, 胡思宇.多尺度熵在轉子故障診斷中的應用[J].振動、測試與診斷, 2013,33(2): 294-297.

ZHENG Jin-de, CHENG Jun-sheng, HU Si-yu.Multi-scale entropy based rotor fault diagnosis[J].Journal of Vibration Measurement & Diagnosis, 2013,33(2): 294-297.

[ 4 ] 鄭近德, 程軍圣, 楊宇.基于多尺度熵的滾動軸承故障診斷方法[J].湖南大學學報: 自然科學版, 2012, 39 (5): 38-41.

ZHENG Jin-de, CHENG Jun-sheng, YANG Yu.A rolling bearing fault diagnosis approach based onmulti-scale entropy[J].Journal of Hunan University:Natural Sciences,2012,39(5):38-41.

[ 5 ] Zhang Long, Xiong Guo-liang, Liu He-sheng, et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference[J].Expert Systems with Applications, 2010, 37(8): 6077-6085.

[ 6 ] Costa M, Goldberger A, Peng C K.Multi-scale entropy analysis of biological signals[J].Physical Review E, 2005, 71 (2): 021906.

[ 7 ] Costa M, Goldberger A, Peng C K.Multi-scale entropy analysis of complex physiologic time series[J].Physical review letters, 2002, 89 (6): 068102.

[ 8 ] Zheng J D, Cheng J S, Yang Y, et al. A rolling bearing fault diagnosis method based on multi-scale fuzzy entropy and variable predictive model-based class discrimination[J].Mechanism And Machine Theory, 2014, 78: 187-200.

[ 9 ] CHEN Wei-ting, WANG Zhi-zhong, XIE Hong-bo, et al.Characterization of surface EMG signal based on fuzzy entropy[J].IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007, 15 (2): 266-272.

[10] Wu S D, Wu C W, Lin S G, et al.Time series analysis using compositemulti-scale entropy[J].Entropy, 2013, 15 (3): 1069-1084.

[11] Yilmaz E.An Expert System Based on Fisher Score and LS-SVM for Cardiac Arrhythmia Diagnosis[J].Computational and Mathematical Methods in Medicine,2013,2013:849674.

[12] Vapnik V N.The nature of statistical learning theory [M].New York: Springer Verlag,1999.

[13] 石志標, 苗瑩.基于FOA-SVM的汽輪機振動故障診斷[J].振動與沖擊, 2014,33(22):111-114.

SHI Zhi-biao, MIAO Ying.Vibration fault diagnosis for steam turbine by using support vector machine based on fruit fly optimization algorithm[J].Journal of Vibration and Shock, 2014,33(22):111-114.

Composite multi-scale fuzzy entropy based rolling bearing fault diagnosis method

ZHENGJin-de1,PANHai-yang1,CHENGJun-sheng2,ZHANGJun1(1.School of Mechanical Engineering, Anhui University of Technology, Maanshan 243032, China; 2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China)

Abstract:To precisely extract the nonlinear fault features from rolling bearing vibration signal, a novel method for measuring the self-similarity and complexity of time series-termed composite multi-scale fuzzy entropy (CMFE) is proposed, aiming at the drawback of the coarse-grained way of multi-scale entropy (MSE).Compared with MSE, CMFE combines the information of multiple coarse-grained sequences and obtains more stable values with a better consistency.Based on the CMFE, Fisher score for feature selection and support vector machines, a new, intelligent rolling bearing fault diagnosis method is proposed.The proposed method is applied to analyze experimental rolling bearing data by comparisons, and the results verify its effectiveness and superiority.

Key words:multi-scale entropy; composite multi-scale fuzzy entropy; feature selection; rolling bearing; fault diagnosis

中圖分類號:TN911.7; TH165.3

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.08.018

收稿日期：2015-05-19修改稿收到日期：2015-08-31

基金項目：國家自然科學基金項目資助(51505002;51375013);安徽省高校自然科學研究重點項目資助(KJ2015A080)

第一作者 鄭近德 男，博士，講師，1986年生

E-mail:jdzhang@ahut.edu.cn