淺談平面方程的五類解法

高燕

鄭州師范學院，河南　鄭州450044

?

淺談平面方程的五類解法

高燕

鄭州師范學院，河南鄭州450044

摘要:根據平面的方程的相關知識，以一道求平面方程的題目為例，總結了求平面的方程的五類解題方法，并從中總結出了一些規律，從而能幫助學生更快的找到求平面的方程相關題目的解題思路。

關鍵詞:平面的方程;總結;解題方法

在空間解析幾何中，平面是最簡單的幾何圖形之一，求平面的方程是一類非常重要的題目。平面方程的形式多樣，知識點多，解題方法靈活多樣，這就導致學生在解題過程中找不到明確的思路。為此，本文以一道題目為例，從五個方向介紹求平面方程的方法。通過不同的求解方法，開闊學生的解題思路，提高綜合應用數學知識的能力。

一、由平面上一點與平面的方位向量決定平面的方程

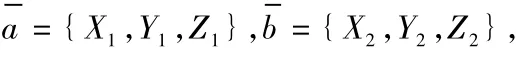
二、由平面上一點與平面的法向量決定平面的方程

總結:要求平面的方程可以從已知條件中找到平面上一點M0(x0， y0，z0)和平面的法向量然后由平面的點法式方程A(xx0) + B(y-y0) + C(z-z0) = 0經過化簡得到平面的一般方程。也可以先設出所求平面的點法式方程A(x-x0) + B(y-y0) + C(z-z0) = 0，由于已知平面過P點，那么要求平面的方程只需要求平面的法向量{ A，B，C}，要求{ A，B，C}只需在已知條件中再找出滿足平面方程的兩個條件就可得到A:B:C的比值，這樣就可得到平面的點法式方程。

三、直接求得平面的一般方程

總結:設出所求平面的一般方程Ax + By + Cz = 0，其中有A，B，C，D四個量未知，從已知條件中只要找到三個條件，就可得到A:B:C:D的比值，那么就可得到平面的一般方程。

四、利用平面束理論求平面的方程

總結:利用平面束理論求平面的方程是一類非常重要的方法，通常可以簡化計算。

五、利用軌跡與方程理論求平面的方程

總結:利用軌跡與方程理論求平面的方程，關鍵是要列出滿足題意的等價關系。

總之，在求解有關平面方程的題目時，可以從這五個大的方向中任選一個方向來尋找解題思路，這樣就可以使學生從紛繁復雜的知識點中抽離出來，使學生能夠盡快找到解題方法。

［參考文獻］

［1］呂林根，許子道.解析幾何(第四版)［M］.北京:高等教育出版社，2006.

［2］黃莉.空間過點與直線的平面方程的求法［J］.職大學報，2014，09:73 -74.

［3］邱云蘭.例析平面方程的幾種解法［J］.韶關學院學報，2010，06:19-22.

中圖分類號:G633.7

文獻標識碼:A

文章編號:1006-0049-(2016)05-0172-01