立足生本謀策略,提高數學學習力
王楓 李衛星

[摘 要] 在尊重生本的基礎上研究初中數學教學策略,可以提升學生的思維品質,進而提升學生的學習力. 教學實踐表明,學生的數學學習力可以在情境化教學中,將數學知識轉換為情境知識,用情境知識去深化數學知識理解;可以在思維方式的培養中、在學習反思的過程中得到提高.
[關鍵詞] 初中數學;生本;教學策略;學習力
當“以學定教”成為一種教學共識時,就需要關注人的存在. 顯然,“以學定教”的潛臺詞是以學生的學來確定教師的教. 這里,我們關注作為學習主體的學生的存在,因而教育理念當中也就與郭思樂教授所倡導的生本理念不謀而合. 立足生本的教學理念,謀取教學的有效策略,具體到初中數學教學中,就可以有效地提高學生的學習力.
這里,首先需要界定幾個關鍵詞:第一,生本. 華南師范大學郭思樂教授首倡這一教學理念,并在全國進行了廣泛實驗,產生了不小的影響,從國家到地方的教育雜志給予了多次推介. 從筆者的視角來看,初中數學必須關注學生對數學知識的主動構建,因而事實上就在關注作為學習主體的學生的數學思維過程,這就是以生為本理念的有效解讀. 第二,教學策略. 教學策略是教學理念作用下的教學思路與教學方法的綜合,介于抽象的教學理念與教學操作之間、兼具理念與實踐的策略性知識,適當的教學策略是教學質量的保證,也是提升學生學習力的重要保障. 第三,學習力. 學習力這一概念最初來自教育發達的國家,近年來成為我國基礎教育界的一個熱門話題. 在初中教育的諸多專著中,其實也有著學習力的影子. 譬如有研究者就指出,“學習力就是指在學習過程中對數學知識的學習態度與接受能力,以及運用數學知識解決實際問題的能力,主要包括專注力、理解力和思維力”. 這樣來自一線教學的理解,也為學習力提供了有益的注腳. 當然,需要說明的是,這樣的闡述更多的是從思維的角度出發的,是從智力的角度出發的. 但無論如何,學習力應當成為初中數學教學研究的一個關鍵詞.
情境教學策略,可迅速提升學
生的學習力
情境教學相對于學習力而言,影響力更為廣泛,但這其中有混用的情形. 新課程標準強調創設學習情境,有人因之演繹為情境教學;我國當代著名教育家李吉林先生研究情境教學數十年,她的情境教學與課程標準所提的情境又有所不同. 筆者這里取課程標準的含義,同時借鑒李吉林先生情境教學的精華,提出在初中數學教學中關注適合學生實際的情境創設,使情境不僅成為引導學生構建知識的條件保障,更成為提升學生學習力的一種有效教學策略.
比如教學“不等式”,蘇教版教材安排在八年級下冊第一章,教材安排了一個例子:某轎車在某公路上行駛的速度是a km/h,已知該公路對轎車的限速是100 km/h,那么兩者關系可以表示為a≤100. 對于這樣的教材設計,筆者以為可以使之進一步情境化. 如通過多媒體呈現一個限速標志牌,而不必作太多的語言說明,并讓學生結合此標牌思考可能存在的數學含義. 事實證明,學生在此過程中,思維起初比較發散,他們會思考公路上有過的其他標志牌,然而片刻之后,學生的思維就會集中到該限速標志牌的含義上來,尤其是在教師提出用數學語言描述該標志牌的含義之后,學生的思維更會努力地將數學與生活聯系在一起,將標志牌上的100 km/h變成學生思維中的a≤100. 這實際上就完成一個從生活到數學的過程. 進而,將這種過程上升到教學策略的角度,就可以告訴學生,在以后的數學學習中,遇到一些生活問題時,要學會用數學語言去描述之.
在筆者看來,這就是一種情境教學的策略,是一種將數學知識轉換為情境知識,用情境知識去深化數學知識理解的策略. 在理解的過程中,學生的思維會經歷數學建模、數學抽象等,這對于學生數學學習力的提升極有好處. 筆者所教的學生常常說的一句話就是,“能夠在我們數學老師的課堂上輕輕松松地學到知識”. 筆者以為,學生所感覺到的輕輕松松,實際上是對情境的一種認可,即感受到了情境在知識構建中的階梯性作用;而學生所說的“學到知識”,更多的是理解了知識,能夠靈活地運用知識去解決問題,這與文首提到的學習力的樸素理解是一脈相承的.
關注思維策略,可為學習力的
提升提供幫助
數學是抽象的學科,數學知識的構建需要思維強有力的參與,無論是構建數學知識,還是利用數學知識去解決實際問題,都離不開思維的高質量活動. 因而,對于思維策略的關注,讓學生學會利用更好的思維方法去看待問題、分析問題、解決問題,實際上就是學習力提供的重要途徑.
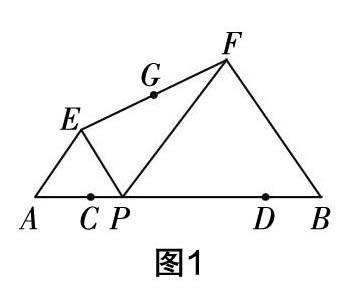
譬如,在解三角形的教學中,筆者有一次給了學生這樣一道題:如圖1,AB=6,C,D是AB上的兩點,且AC=DB=1,P是線段CD上一動點,在AB同側分別作等邊三角形APE和等邊三角形PBF,G為線段EF的中點,點P由點C移動到點D時,點G移動的路徑長度為______.
這種動態類的題目往往是初中生比較頭疼的題目,因而在數學教學中也極具生命力. 這種題沒有新老之分,無論是在學生的新知學習中還是階段復習甚至中考復習中,都具有發揮價值的地方,這里所說的發揮價值,即是培養學生思維、形成思維策略的價值.
求解本題的關鍵是根據題意,依據動點的運動去延長AE,BF交于點H(如圖2). 這樣就可以得出∠A=∠FPB=60°,其后借助相關的平行關系與已知的角度得出四邊形EPFH為平行四邊形,在此基礎上根據EF與HP相互平分,最終得到點G的移動路徑長是2.
在這樣的解題過程中,學生的思維能否集中到作出這么多的輔助線上,成為能否成功解決的關鍵. 事實上筆者發現,相當一部分學生即使在筆者提供了解題方法之后仍然感覺不可思議,因為在他們的思維中就沒有這么多輔助線出現過的情形,這也暴露了學生的思維中數學形象更多的是簡單形象. 本題輔助線雖多,卻并不復雜,關鍵是學生的思維是否能夠邁開這一步. 因此,與其說這是一個考查思維的題目,不如說是同時考查思維與思維方式的題目. 初中數學要利用類似的題目去打開學生的思維空間,讓學生建立起數學問題的解決不受狹隘經驗所限的認識,一旦這種思路形成,一些數學問題的解決往往都能獨辟蹊徑. 這事實上也是學習力提升的重要表現.
在日常教學中我們經常看到的一種情形就是,學生在面對稍微復雜點的數學問題時,往往思路打不開,這實際上就是學生的思維受限的緣故,而其背后的原因就是思維方式的訓練不夠廣泛且沒有得到應有的重視,這也客觀上造成了學生的學習力不夠.
培養學習習慣,可為學習力的
提升提供保障
學習習慣相對于思維來說是非智力因素,但在教學中我們又發現,學生的學習習慣對學習力的提升有著顯著的影響. 很多學生的數學成績不理想,并不是智力不夠,恰恰是因為學習習慣不好. 因此,筆者以為,需要建立一種認識,那就是提升學生的學習力,除了要從智力角度入手,還要從非智力因素入手,而學習習慣就是至關重要的非智力因素.
初中數學的學習習慣很多,在筆者看來,最重要的就是培養學生反思的習慣. 反思意味著不是做一題扔一題,意味著不是只關注數學知識的構建結果而忽視構建過程. 反觀學生的學習實際,恰恰是做一題扔一題,結果就是做一題忘一題,恰恰是只關注數學公式、數學規律,而不關心這些公式和規律是怎么得來的,這種只知道向前看,不知道反思知識構建過程的習慣,極大地束縛了學生學習力的提升. 在近些年的教學中,筆者致力于讓學生在數學知識學習之后去反思其是怎么得來的. 如教學“等腰三角形的性質與判定”(蘇教版九年級上冊),不僅關注性質與判定,更關注性質是如何得到的,判定定理是如何形成的,以及為什么自己的有些思路無法成為判定依據. 對于這些問題的反思,可以讓學生在掌握知識時更有深度,從而提升學習力.
綜上所述,學習力對于初中數學教學來說不是一個可有可無的概念,而應成為當下推進有效教學的“牛鼻子”,因此,在教學中要高度關注、致力研究. 樹立了這一理念,就是真正的以生為本!

