新課程下高考中函數概念的易錯點剖析

孫明俠

函數的概念在高考中占很大比重，在《2016年普通高等學校招生全國考試大綱》中對函數概念的要求是：了解構成函數的要素，會求一些簡單函數的定義域和值域；了解映射的概念。在實際情境中，會根據不同的需要選擇恰當的方法表示函數；了解簡單的分段函數，并能簡單應用。理解函數的單調性、最大值、最小值及其幾何意義；結合具體函數了解奇偶性的含義。會運用函數圖象理解和研究函數的性質。

函數是高考中非常重要的內容，它是高中生數學學習的一條主線，也是高中數學的核心知識，高考數學的大部分內容都與函數有關，都要用到函數思想方法。

盡管高中數學函數的內容和教學方法被不斷的完善，但是高中生在函數學習中仍然存在很多困難。因此，筆者通過實地調查，探究高中生在函數學習的過程中在函數概念存在的易錯點，并對高中生函數函數概念學習困難的原因進行分析，以幫助數學教育工作者在備考中獲取真實的學習情況反饋信息，希望能夠幫助函數學習困難學生，使他們在高考中有所收獲。

1導言

1.1選題背景

1962年，萊布尼茲（Gottffied Wilhelm Leibniz）首次使用“function”來表示函數（冪）。1755，歐拉（Leonhard Euler）第一次用變量來定義函數，他的函數定義就是初中學習函數的觀點，即應用“變化運動”的觀點來研究函數。在此之后，數學界對函數概念的定義發生了五次變革。直到康托（GeorgCantor）創立的集合論在被數學界普遍認可后，維布倫（Ve-blen）第一次用“集合”與“對應”的概念為近代函數定義，這就是如今高中函數學習的內容。其中集合的概念使得函數的三要素——對應法則、定義域及值域實現具體化，而且打破了“變量是數”的限制。

函數是近現代的數學的基礎，是高中數學學習中最重要，也最復雜的概念。現階段正處于新課改的實踐與探索階段，高中函數教學研究已成為中學甚至高校數學教育教學的研究重點。

2國內外研究現狀

2.1函數的相關研究

關于函數的相關研究方面，筆者發現國內學者分別從函數的概念、三要素等方面進行的相關研究。

朱文芳（1990）在論文中從心理學的角度對高中生函數概念的學習困難做了分析，她分別從概念的形成水平、數學氣質類型和數學思維發展水平這三個方面，通過大量分析，得出了結論：學生學好函數的概念的重要性。

邢鐲（2013）研究了要求高中學生掌握的指數函數、對數函數、冪函數、三角函數等函數進行了有限次有理運算，或者將這些函數進行有限次復合，最終得出新函數的過程。他闡述了高考對函數的相關知識的考查范圍和要求，本質上都是對函數的概念、圖像和性質的考察。

2.2學習困難的相關研究

筆者發現關于函數學習困難研究的文獻并不是很多，其中比較有代表性的有下面這些文章：

裴利芳（1995）分別從知識結構、學習的認知加工水平、元認知技能對學習的影響進行有關“學習困難”的研究。主要是對學生的學習困難心理因素從“認知結構的角度”進行分析。

劉兵（2013）根據自己的實際教學經驗，分別從學生自身因素、函數本身特征、教師因素三方面對高中生函數學習困難的原因分析做出了歸納。

3研究方法

3.1研究對象

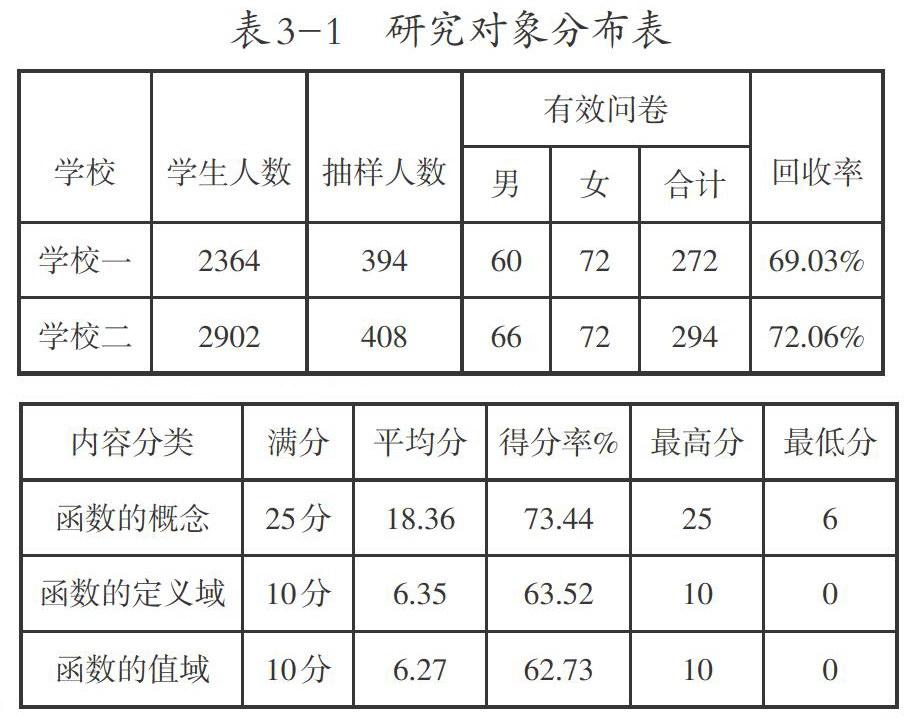
為了保證調查樣本的普遍性，本研究選擇吉林省長春市的兩所具有代表性的高中進行調查，記為學校一和學校二。

4高中生函數概念學習困難分析

4.1總體情況分析

4.1.1高中生函數概念學習困難的整體情況分析

為了了解高中生在函數概念學習過程中存在哪些困難，筆者將學校一和學校二學生在函數的不同知識維度上得分情況統計成表4-1-1：

相對而言，高中生掌握最好的是函數的概念。由于函數概念與函數的定義域和值域本質上是同一個問題，所以學生在這兩方面的掌握情況也比較不錯。

4.2高中生函數概念學習的主要困難

筆者通過對調查問卷結果分析、學生訪談記錄整理以及課堂教學觀摩和實踐，意識到現階段高二和高三學生對函數的概念、定義域和值域情況并不樂觀，筆者將學生在函數學習中存在學習困難類型總結如下：

4.2.1函數概念的理解和表征困難

函數的概念是高中數學中最重要的概念之一，數學教學之所以強調對函數概念的理解和掌握，主要原因是數學的學習和理解，究其根本是對于概念的理解。筆者通過對調查問卷的分析和整理，總結出學生在函數概念學習中主要存在以下兩類學習困難：

4.2.1.1函數的概念記憶困難

高中階段要求分為記憶和理解兩個階段來學習函數概念，之所以強調函數概念記憶的準確性，是因為高中對于函數概念的定義與學生在初中學習到的定義有所不同。初中是用“運動變化”的觀點來定義函數，即“在某個變化過程中，有兩個變量x，y，如果給x一個值，就有唯一的y與它相對應”，而高中是從“集合與對應”的角度定義函數的。學生是否能夠接受函數新的定義方式是筆者調查的主要目的。通過對學生調查問卷的分析，筆者發現大部分同學雖然無法將函數概念準確的表述出來，但是很多學生能夠從對應的角度理解函數的概念：

【問題1】函數的概念

這類學生是從集合的角度來描述函數的概念的，他們對函數概念的理解比較準確，表述過程也相對完整。

但是部分同學對于函數的定義來源并不明確，比如通過對下面這名同學的理解過程可以看出，部分學生對于函數概念的理解過于表面化。定義域是指函數中自變量的范圍，而在函數定義中還沒有明確自變量，因此更無從談及定義域，解答過程如下所示：學生的得分情況：

有的學生對函數概念的理解還限于初中的理解水平，仍然將函數的定義理解為變量與變量的相應關系：

對于產生這類學習困難的學生，教師應該明確指出高中函數的理解角度，否則他們將很難理解函數的意義，并無法在日后的學習中觸類旁通。

4.2.1.2函數概念的理解困難

對于數學知識，尤其是函數知識，學生僅僅可以對函數的相關知識進行復述是遠遠不夠的，要想完全理解函數的概念，還需要在不同的函數表征方式中正確辨析，見本調查中的問題2：

【問題2】以下問題中哪些表示y是關于x的函數

本題要求學生判斷以上表征中是否是函數，在這10個小題中，涉及到的函數表征方式有圖像、表格和解析式。學生的判斷依據是函數的概念，即有關函數概念程序性知識的應用。從學生的得分情況可以看出，學生在他們常見的（2）、（4）、（5）三類函數中不存在辨析困難，得分率均達到100%；對于（3）、（6）、（7）三類函數只有部分學生出現辨析錯誤，但是得分率也在95%以上；比較值得注意的是（1）、（8）、（9）、（10），這些題學生由于沒有抓住函數概念中“任意x都有唯一y與之相對應”這一精髓，所以出現了判斷錯誤。

4.2.2函數定義域的優先考慮困難

在本調查中，盡管有些題目不是直接考察函數的定義域，但是筆者發現學生出現錯誤的原因卻出于對函數定義域的優先原則考慮不周。筆者將學生在解題中出現這類錯誤的題目總結在一起，并統計了每道題的正確率，以方便通過學生的答題結果分析比較，具體見下表：

4.2.2.1定義域

函數的定義域作為函數的三個基本屬性之一，是很多問題的研究基礎，因此學生能否準確掌握函數的定義域求法是高中函數的必考問題之一。

本題正確人數410人，正確率為72.44%。從調查結果來看，學生對于函數定義域的掌握還有待加強。筆者將學生出現的各種錯誤進行了歸類和總結，具體有以下兩種：

其中一部分同學雖然懂得對自變量的某些限制加以分析，明確被開數必須是非負數，但卻沒有注意到被開方數同時作為分式的分子，因此也就出現了這樣的錯誤：

另外一部分同學不僅出現了上述錯誤，還由于審題不仔細而沒有注意到題目中要求將答案用區間表示：

綜合以上，可以發現函數定義域的相應考點對學生來說并不陌生，只是在具體解題時學生容易顧此失彼，或者沒有按照題目的要求作答。

4.2.2.2求值域

函數的三個基本屬性包括函數的定義域、對應法則和函數的值域。其中定義域是求函數值域的基礎，但是筆者通過研究調查問卷發現學生在求函數值域時常常忽略對定義域的考察。本研究中問題4就反映了這一現象：

本題考察的是求函數的值域，正確人數336人，正確率為59.36%。筆者發現高二和高三學生對于函數值域的掌握情況比較樂觀，學生關于本題的求法有以下兩種，一類是通過直接判斷函數的單調性來求函數的值域。另一類學生利用導函數的相關知識，結合導函數的正負判斷函數的單調性和最值，從而得出函數的值域：

盡管大部分同學都掌握了函數值域的求法，但是本題的得分率依舊不高的原因是學生忽略了對函數定義域的考察：這類學生的解題思路完全正確，但是由于定義域的求解錯誤導致值域的解題困難，所以函數定義域的優先考慮尤為重要。

4.2.2.3圖像

本題的正確人數為490人，正確率是86.57%本題學生有兩種解法，一種是現根據原函數寫出反函數的表達式，然后代值：

還有一種解法是直接將原函數與反函數的x和y值對調：

這兩種解題思路都是正確的，相比之下不難看出，應用反函數的定義域與原函數值域的關系更利于解題。

4.3高中生函數概念學習困難成因分析

4.3.1初高中銜接問題

對于函數部分的知識高中學生并不陌生，學生在初中就已經對函數知識有簡單的了解，相當一部分同學在訪談中還表示他們初中階段對函數的理解掌握得還算不錯，但是到了高中就意識到初高中函數內容銜接問題成為這部分學習的一道鴻溝。調查結果顯示，初高中銜接問題是學生函數學習困難的首要因素。初中函數的相關知識簡單易懂，而高中函數立足于一個新的起點。就二次函數而言，它初中函數中屬于最難的知識，但在高中卻作為最基本、最典型的函數類型來研究，對于函數定義域、值域、單調性等許多抽象的相關概念需要借助二次函數來完成，這對于剛剛接觸高中數學的學生來說是一個不小的跨度。關于初高中銜接的問題，以函數概念為例，有以下三點區別：（1）定義方式不同。從初中運動變化的觀點下傳統的函數概念，到高中函數是以集合與對應觀點定義的近代概念。（2）函數概念理解的跳躍性。初中階段，教師對“變量”的解釋是“變化的量”，這樣解釋僅僅停留在概念的表面。（3）對于學生已有的認知水平的一個挑戰是用集合、對應的觀點去理解函數關系，此時的學生尚未從初中的學習思維中跳出來，缺乏用函數思想分析問題和解決問題的能力。

4.3.2高中學生思維發展水平的局限性

筆者通過對受訪學生的個人訪談得知函數的學習困難與高中學生思維發展水平有關。原因之一是學生的思維發展水平還沒有從具體形象思維過渡到抽象邏輯思維。高中數學課程要求學生的思維集中于抽象邏輯思維活動空間，但是對于更多的學生而言，學生只能對于抽象邏輯思維活動的訓練尚未成熟，他們更大程度上仍然需要依賴具體形象的材料來理解抽象的邏輯關系。這就造成了學生思維發展水平相對于應用范圍略顯滯后的結果。

除此之外，學生要想學好高中函數，必須掌握的技能就是把動態的函數演變過程轉化為靜態的獨立對象，對學生的辯證思維水平要求較高。高中對學生的思維發展水平要求的是從具體形象思維逐步過渡到抽象邏輯思維，在這樣的思維過渡階段，學生的辯證思維很難達到一個新的跨越。不過，在函數學習過程中具有這樣不可替代的困難性和思維上的跳躍性，才使它成為高中生數學學習中不可替代的部分，也成為訓練學生邏輯抽象思維和辯證思維的最佳訓練工具。

函數概念是高考中考察的重點內容，通過對高中生在學習的過程中，函數概念存在的易錯點剖析，以幫助數學教育工作者在備考中獲取真實的學習情況反饋信息，希望能夠幫助函數學習困難的學生在高考中有所收獲。