磁浮直線電機的等效控制模型改進

于天劍， 陳特放， 鄧江明， 陳雅婷，成　庶

(中南大學 交通運輸學院, 410075 長沙)

?

磁浮直線電機的等效控制模型改進

于天劍， 陳特放， 鄧江明， 陳雅婷，成庶

(中南大學 交通運輸學院, 410075 長沙)

摘要:為準確測量電機參數，提出一種新的改進的SLIM等效電路參數辨識方法，利用不同頻率時的電機推力、變頻器輸出電壓和電流等靜態堵轉特性，結合算法推算出適合控制用的SLIM等效電路中的初級電阻、漏感、次級等效電阻和漏感參數. 通過MATLAB仿真實驗，結果表明各動態參數幅值的修正對提高電機速度辨識精度是有利的，并在中低速磁懸浮模擬實驗平臺上進行實驗，驗證了在改進后的T-模型下，對結果分析可以得知電機的狀態辨識效果和精度得到了提高，并對以后的電機參數設計具有指導意義.

關鍵詞:SLIM； 等效電路； 參數設計； MATLAB仿真； 磁懸浮實驗平臺

目前中低速磁懸浮的驅動系統普遍采用單邊短初級長次級直線感應電機，電機運行時，初、次級保持一定的機械間隙，其速度檢測也不同于旋轉式電機，現有的速度檢測方法有雷達定位[1]、計量軌枕和交叉感應回線[2]等，這些方法都必須鋪設專門的檢測和支撐設備，測速成本高、維護麻煩，因設備故障或外部干擾導致電機控制失敗時有發生[3-4]. 因此研究單邊直線感應電機(SLIM)的無速度傳感器控制很有價值，目前針對SLIM 的研究主要集中在等效電路參數、邊端效應補償及推力法向力特性等方面[5-6]，文獻[4]提出一種采用BP神經網絡的SLIM 速度估算方法，但網絡訓練樣本獲取復雜且無法滿足電機的動態控制要求；文獻[7]研究了直線感應電機的無速度傳感器直接磁場定向控制并未針對SLIM特有的邊端效應進行有關參數補償，當互感參數減小時，估算偏差較大. 在本文中討論了SLIM在實際運行工況下的橫、縱向動態端部效應和“集膚”效應對電機氣隙磁場的影響，將分析得到的結果統一到對電機T-模型的改進上，并導入與電機幾何尺寸、次級導體材料、和滑差率有關的4個改進系數. 利用改進的SLIM T-模型，可以修正計算與觀測器設計有關的各動態參數. 通過在中低速磁懸浮模擬實驗平臺上進行的兩個方面的實驗,驗證了采用改進后的T-ECM，電機的辨識速度在動態響應過程和穩態精度方面都能獲得滿意的性能.

1電機等效模型改進過程分析

依據麥克斯韋(Maxwell)電磁場方程組[8-9]可得電流層函數為

式中δ′為電磁氣隙，即δ′=kδkδ，δ為初次級鐵芯表面之間的距離，j1、j2分別為初級和次級的線電流密度矢量. 因為電流被假設成無限薄，只有z分量，故矢量磁位A也只有z分量，Az為磁位的z分量，Ez為電場強度的z分量，By為氣隙中磁通密度的y分量. 可得

其中：σs次級電導率，σs=σd，σ次級導體體積電導率，d導體厚度；次級導體沿著坐標x的移動速度為vm. 可進一步得到

(1)

因為初級電流按照周期ejωt隨著時間t變化，可進一步設矢量磁位

(2)

將式(2)代入式(1)，求得全解為

(3)

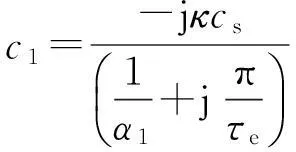
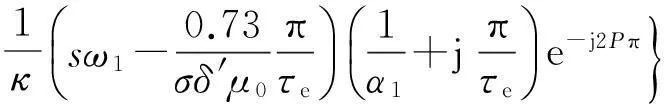
1.1考慮縱向動態端部效應的有關參數改進

氣隙感應電場強度z分量的計算公式[10]為

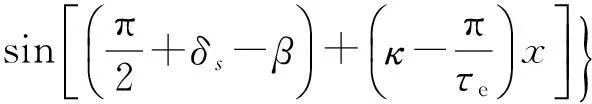
再設R2(s)和Xm(s)為計及縱向端部效應時的歸于初級的次級相電阻和初級每相磁化電抗，于是，結合各式可得

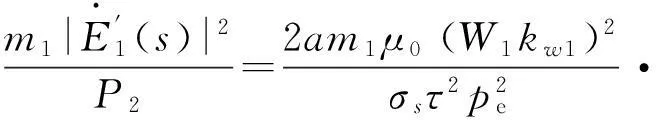
(4)

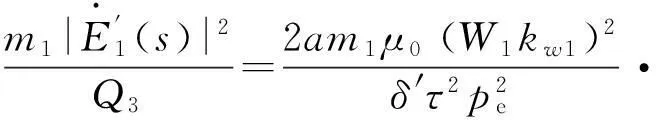
(5)

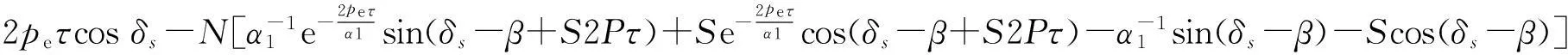
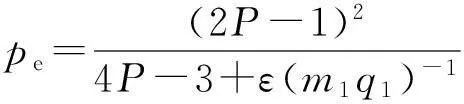
令Kr(s)和Kx(s)分別為次級相電阻和初級每相磁化電抗的縱向端部效應改進系數，由式(4)、(5)可得考慮縱向動態端部效應的直線感應電動機等效電路動態參數改進如下.

式中相關系數Kr(s)和Kx(s)的詳細表達為

1.2考慮第2種橫向端部效應的有關參數改進

設每極磁通為φ(t)，則根據直線電機的邊界結構，有

(6)

求解式(6)可得

(7)

由于初級每相磁勢的瞬時值為

(8)

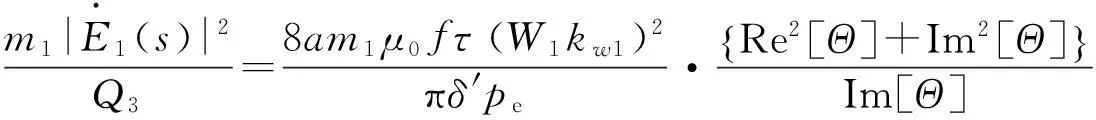
式中各相關系數：

各參數是由場路復量功率相等的關系直接計算出來的，故所有計算結果延續了電磁場分析的嚴謹性.

1.3考慮集膚效應的影響

設kf為“集膚”效應系數[11]，由文獻[11]直接給出其計算公式：

式中：

可知

系數kf反映了“集膚”效應對次級電阻的影響，考慮初級電阻R1和初級漏抗X1，初級每相電阻為

式中：Lcp為繞組半匝平均長，Lcp=2a+Le，Le為初級繞組端部長Le=1.4τ，SA為導向截面積.

初級每相總漏抗為

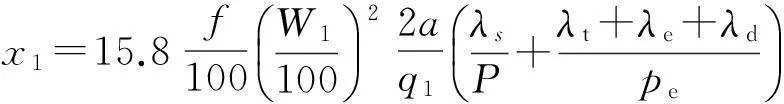
2改進的SLIMT-型等值電路模型特性

通過上述分析可以得到端部效應影響的SLIM改進等值電路T-模型[12]，如圖1所示.

改進后的T型等值電路與普通旋轉感應電動機的等值電路依然相似，所不同的是前者多了由端部效應引起的4個改進系數Kr、Kx、Cr、Cx. 這4個系數都是電機幾何尺寸、次級導體材料和滑差率的函數. 利用這4個改進系數，就可以像計算普通RIM的特性一樣計算SLIM的各種特性(在恒流源或恒壓源調節模式下)[13].

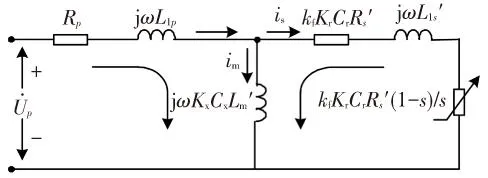
圖1考慮各類端部效應影響后的SLIM等效電路改進T-模型

2.1T-模型改進后各參數的相應調整

根據圖1的電壓電流回路方程，應用基爾霍夫電壓定理，可得

次級的電磁有功功率輸出

可得

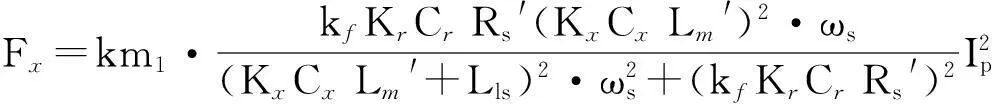
(9)

定義3個自由系數Ax，Cx和Dx，式(9)簡化為

(10)

式中，各系數調整為

對應式(10)的最大推力輸出點的最優滑差頻率以fs,optimum(Hz)標記，也需要作相應的計算調整為

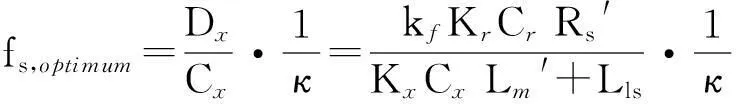
次級等效感應電阻Rs′互感參量Lm′作相應的計算調整如下:

2.2觀測偏差對輸出性能影響的仿真分析

SLIM最終的電磁推力輸出精度將直觀反映為初級電流的重構精度上，又可將實際電流與重構電流的差別分為幅值不匹配和相位不匹配兩方面[7,14]，并從這兩個點及其組合上分別討論觀測偏差對輸出推力的最終影響. 為便于觀察并考慮實際運行工況，仿真實驗取電流參數：幅值偏差0.05 A/0.1 A，相位偏差(π/20)/(π/10)，相關實驗結果如下.

實線為電流為0.6 A 虛線電流為0.5 A

圖2　重構電流與實際電流幅值不匹配

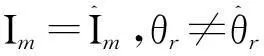
圖3重構電流狀態與實際電流相位不匹配(Δθr=π/20或π/10)

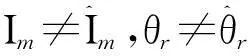
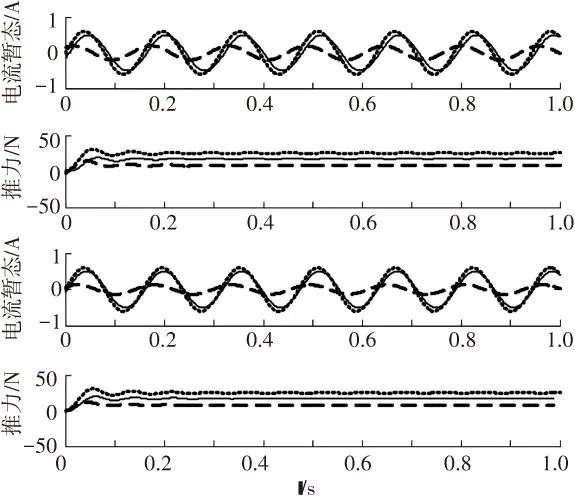
(a) ΔI=0.1 A， Δθr=π/20或π/10

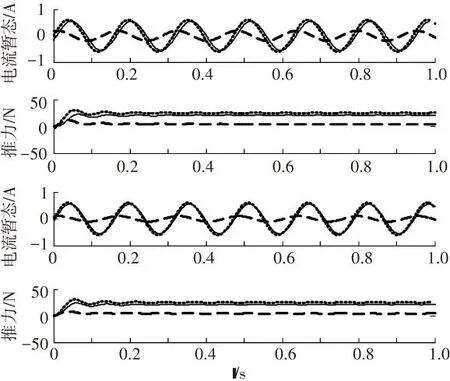
(b)ΔI=0.05 A，Δθr=π/20或π/10

圖5　重構電流狀態瞬時不匹配偏差特性

圖5 (a)中實線電流為0.55 A，相位為0；虛線電流為0.6 A,相位為0. 圖5(b)中推力實線電流為0.55 A，相位為π/10；虛線電流為0.6 A,相位為0. 圖5(c)中實線電流為0.6 A，相位為π/10; 虛線為0.6 A，相位為0. 圖5(d)中實線電流為0.6 A，相位為π/20; 虛線電流為0.6 A，相位為0.由圖2～5仿真實驗結果可知，SLIM電流辨識狀態對輸出電磁推力的辨識精度主要的影響在于電流幅值的辨識差別，電流相位偏差都可以在累計積分計算中逐步消除. 本文采用縱、橫向端部效應的影響來改進電機的等值計算模型，目的是為了改進相應的幅值計算參量，這樣即能實現辨識電流與實際控制電流的較小偏差，也實現了對精度的提高.

3磁浮模擬平臺實驗

模擬磁懸浮驅動的直線電機牽引系統實驗平臺如圖6所示.

圖6　磁懸浮直線電機牽引系統實驗平臺

通過采用改進T-模型后電機的算法進行實用性驗證. 該實驗平臺的驅動懸浮控制原理與中低速磁懸浮系統基本原理是一樣的，但結構尺寸不同，所研究的控制算法具有通用可移植特性. 對于邊端極磁場畸變及不規則發散狀態，等價為電流狀態值在實數變化區域映射到雙曲正切函數上[15]. 因此，本文需要對前文獻[14]中公式稍加修正為

其中，對任意實數區域的輸入狀態υ(t)，均滿足：|arctanh(υ(t))|<π/2.

圖7～9為模擬實驗臺的應用實驗結果，其中各示波器所得動態波形中：通道1(CH1)為實測電流狀態(表征實際速度)，通道2(CH2)為辨識重構電流狀態(表征辨識速度)，通道M(M)為狀態偏差信號(表征估算偏差).

實驗結果分析：1)采用修正的正定濾波矩陣Γ以后，見圖7，電機穿越邊端極磁場區域電流的發散狀態被有效抑制，電流重構狀態不論是幅值還是相位上與實際狀態也基本吻合；2)考慮SLIM的端部效應及“集膚效應”并對電機的等效控制電路進行改進以后，并引入了修正以后的各類動態參數計算，電機重構的輸出狀態與實際輸出狀態，不論是低速還是高速恒定運行工況下，還是加減速的動態變化區域，相互偏差都很小如圖8、9所示.

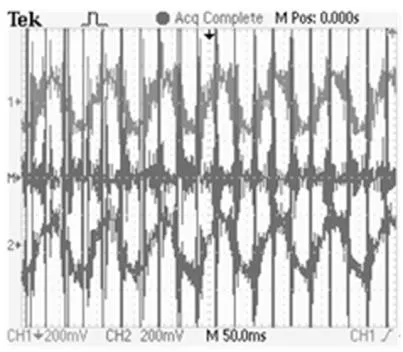
(a)修正Γ前

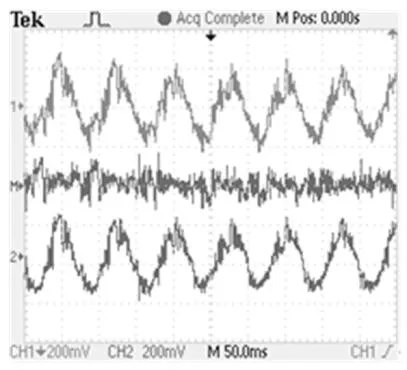
(b)修正Γ后

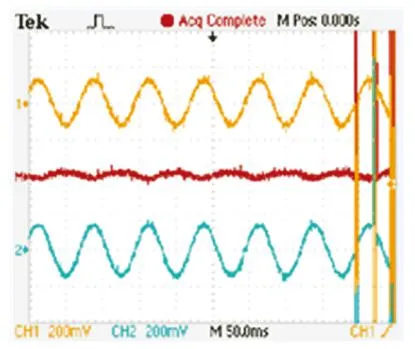
(a)修正Γ 前

(b)修正Γ 后

狀態偏差越小在實際的慣性牽引中，電機的速度辨識精度越高，從而表明了改進電路拓撲以后各控制算法的性能都有了一定程度的提升.

(a)由中速區向高速區加速

(b)由高速區向中速區減速

圖9采用改進T-模型以后電機突變速度運行工況下，重構狀態與實際輸出狀態動態波形

4結論

1)在對電機的T-型等效電路的改進的基礎上，并引入與電機幾何尺寸、次級導體材料、和滑差率有關的4個改進系數Kr、Kx、Cr、Cx，利用改進的電機T-模型，并提高了其品質因數，且不影響SLIM在無速度傳感器策略下的可觀性.

2)通過仿真實驗，表明各動態參數幅值的修正對提高電機速度辨識精度是有利的. 在中低速磁懸浮模擬實驗平臺上進行兩個方面的實驗驗證：結合互聯觀測器設計原理，重新修正了正定等效濾波矩陣Γ，使得SLIM即使在穿越磁場畸變區域，也能夠獲得良好的電流狀態觀測；驗證了在改進后的T-模型下，電機的狀態辨識效果，表明重構電流狀態，不論在動態變化過程還是穩態精度，基本能夠復現實際電流狀態，也即電機的辨識速度精度已經達到了較高程度.

參考文獻

[1] CHEN W H, BALANCE D J, GAWTHROP P J.et al. A nonlinear disturbance observer for robotic manipulators [J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932-938.

[2] ALFREDO M G, THOMAS A L, DONALD W N. A new induction motor V/f control method capable of high-performance regulation at low speeds [J]. IEEE Transactions on Industry Applications, 1998, 34(3): 813-821.

[3] LIU H X, LI S H. Speed control for PMSM servo system using adaptive functional control and extended state observer [J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1171-1183.

[4] SHIN H B, PARK J G. Anti-windup PID controller with integral state predictor for variable-speed motor drives [J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1509-1516.

[5] 黃堅,郭中醒.實用電機設計計算手冊[M].上海:上海科學技術出版社,2010:233-238.

[6] AMIR Z B, MOHAMMAD R N, MOHAMMAD R M. Optimum design of single-sided linear induction motors for improved motor performance [J]. IEEE Transactions on Magnetics, 2010, 46(11): 3939-3947.

[7] YU Xinghuo, WANG Bin, LI Xiangjun. Computer-controlled variable structure systems: the state-of-the-art [J]. IEEE Transactions on Industry Information, 2012, 8(2): 197-205.

[8] 斯蒂芬·查普曼.電機學[M].5版. 劉新正,譯.北京:電子工業出版社,2012:56-63.

[9] SHIRI A, SHOULAIE A. Design optimization and analysis of single-sided linear induction motor, considering all phenomena [J]. IEEE Transactions on Energy Conversion, 2012, 27(2): 516-525.

[10]BOLOGNANI S, PRETTI L, ZIGLIOTTO M. Design and implementation of model adaptive control for electrical motor drives [J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1925-1936.

[11]KIM D K, KWON B I. A novel equivalent circuit model of linear induction motor based on finite element analysis and its coupling with external circuits [J]. IEEE Transactions on Magnetics, 2006, 42(10): 3407-3409.

[12]VACLAVEK P, BLAHA P. AC induction machine speed observer with rotor resistance adaptation [C]// Proc 16th IFAC World Congress. Praha, Czech Republic:International Federation of Automatic Control Press, 2005:1728-1734.[13]鄧江明,陳特放,唐建湘.單邊直線感應電機動態最大推力輸出的滑差頻率優化控制[J].中國電機工程學報,2013,33(12):123-130.

[14]GINOYA D, SHENDGE P B, PHADKE S B. Sliding mode control for mismatched uncertain system using an extended disturbance observer [J]. IEEE Transactions on Industrial Electronics, 2014, 61(4):1983-1992.

[15]THOMAS J, HANSSON A. Speed tracing of a linear induction motor-enumerative nonlinear model predictive control[J]. IEEE Transactions on Control Systems Technology, 2013, 21(5): 1956-1962.

(編輯魏希柱)

The improvement of equivalent control model research on the maglev linear motor

YU Tianjian, CHEN Tefang, DENG Jiangming, CHEN Yating, CHENG Shu

(School of Traffic and Transportation Engineering, Central South University, 410075 Changsha, China)

Abstract:In order to measure the motor parameters. This paper presents a new and improved SLIM equivalent circuit parameter identification, the motor thrust using different frequencies, the inverter output voltage and current, static stall characteristics, combined with suitable control algorithms calculate the equivalent circuit of SLIM primary resistance, leakage in ductance, secondary equivalent resistance and leakage inductance parameter. By finite element simulation experiments show that the amplitude of the dynamic parameters of each amendment to increase the motor speed identification accuracy is beneficial, conduct experiments on low-speed maglev simulation platform, validated under T-improved model, the motor status identification results show the current state of reconstruction, not only in the dynamic process of change or steady-state accuracy, and has a guiding significance to the future design of motor parameters.

Keywords:SLIM; equivalent circuit; parametric design; MATLAB simulation; levitation experiment platform

中圖分類號:TM359.4

文獻標志碼:A

文章編號:0367-6234(2016)03-0171-07

通信作者:成庶，6409020@qq.com.

作者簡介:于天劍(1988—), 男，博士研究生;

基金項目:國家自然科學基金(61273158).

收稿日期:2014-12-26.

doi：10.11918/j.issn.0367-6234.2016.03.029

陳特放(1957—), 男，教授，博士生導師.