“行程問題中的數(shù)量關(guān)系”教學(xué)思考

費建鋒

一、學(xué)情分析

1.新舊人教版中行程問題教學(xué)內(nèi)容編排不同。

四上舊版的人教版教材中，行程問題的學(xué)習(xí)是滲透在三位數(shù)乘兩位的“口算”和“筆算”教學(xué)中的，比較淡化“行程問題中的數(shù)量關(guān)系”的教學(xué)。

現(xiàn)行的人教版教材中，行程問題的數(shù)量關(guān)系是專門設(shè)立一節(jié)單獨的課，而且安排在三位數(shù)乘兩位數(shù)整個單元教學(xué)的末尾。

從以上兩個版本的對比可以說明，現(xiàn)行的人教版教材更加注重數(shù)量關(guān)系的教學(xué)。舊版主要側(cè)重乘法的計算與算理，在乘法計算中滲透行程問題的數(shù)量關(guān)系；而新版中比較側(cè)重數(shù)量關(guān)系的教學(xué)，利用數(shù)量關(guān)系來幫助學(xué)生解決問題，加深理解它們之間的關(guān)系。

2.學(xué)生已有解決此類問題的能力，怎么教學(xué)。

發(fā)現(xiàn)學(xué)生基本能用算式正確表示，全班42名學(xué)生，前測了之后，40名學(xué)生的列式解答是正確的，正確率95%。在數(shù)量關(guān)系的表達(dá)上學(xué)生有些問題，對班級學(xué)生的表達(dá)情況做了一個統(tǒng)計：

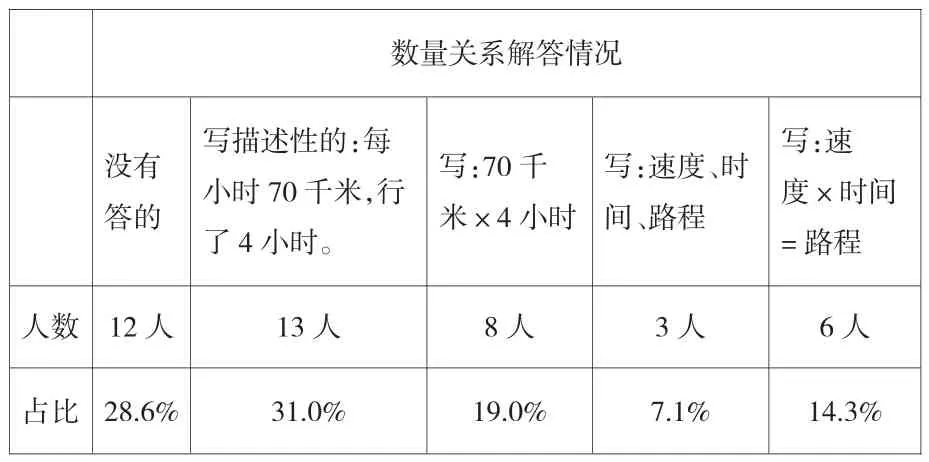
數(shù)量關(guān)系解答情況沒有答的寫描述性的：每小時70千米，行了4小時。寫：70千米×4小時寫：速度、時間、路程寫：速度×?xí)r間=路程人數(shù) 12人 13人 8人 3人 6人占比 28.6% 31.0% 19.0% 7.1% 14.3%

教學(xué)內(nèi)容學(xué)生早有接觸：類似這樣的行程問題，學(xué)生早已比較熟悉了，在二年級學(xué)習(xí)了時間單位之后，就接觸過這樣的問題，尤其是到了三年級，學(xué)習(xí)了兩位數(shù)乘一位數(shù)后，這樣的題目更是遇到的多了。因此，對于行程問題學(xué)生并不陌生，生活中也是經(jīng)常遇見。

知識基礎(chǔ)學(xué)生已有學(xué)過：在此之前，學(xué)生已經(jīng)學(xué)完了整數(shù)的乘法計算，除數(shù)是一位數(shù)的除法，所有的長度單位知識和時間單位知識。

數(shù)量關(guān)系以往有所滲透：通過訪問學(xué)生的形式，我們發(fā)現(xiàn)，數(shù)量關(guān)系的教學(xué)，在以往的教學(xué)中教師是有所滲透的，一些學(xué)生答到“這樣的數(shù)學(xué)關(guān)系，我們老師以前講過的。”也有一些學(xué)生講到“我們老師以前沒有講過，所以我不知道什么是數(shù)量關(guān)系。”

3.針對實際學(xué)情，對教學(xué)內(nèi)容提出新的疑問。

問題1：類似這樣的教學(xué)內(nèi)容，學(xué)生早有知曉，我們的課堂教學(xué)該如何去組織？難道像練習(xí)課或復(fù)習(xí)課這樣去鞏固一遍嗎？

問題2：學(xué)生已有這么高的教學(xué)起點，又該如何去拓展，拓展到何方呢？

二、學(xué)習(xí)路徑

1.理清數(shù)量關(guān)系的表述層次。

《數(shù)學(xué)課程標(biāo)準(zhǔn)》中講到，數(shù)學(xué)是研究數(shù)量關(guān)系和空間形式的科學(xué)。顯然，研究數(shù)量關(guān)系就是在研究數(shù)學(xué)，也說明了數(shù)量關(guān)系在數(shù)學(xué)學(xué)科中的重要地位。數(shù)量關(guān)系在整個小學(xué)階段，就其概括程度，可分為具體、專用、抽象的數(shù)量關(guān)系，要求學(xué)生的表述也是有所側(cè)重的，在低中段學(xué)生中，要能理解或表述具體情境中的數(shù)量關(guān)系，而到中高段需要學(xué)生概括出不同的數(shù)量關(guān)系，最后掌握這些數(shù)量關(guān)系的結(jié)構(gòu)模型。

（1）具體的數(shù)量關(guān)系。

具體的數(shù)量關(guān)系就是從具體內(nèi)容中列出具體數(shù)量關(guān)系式，學(xué)生在理解題意的基礎(chǔ)上能夠表達(dá)這樣的數(shù)量關(guān)系。

如：每件衣服價格×件數(shù)＝衣服總價；

每排的人數(shù)×一共有幾排＝一共的人數(shù)；

汽車每小時行的路程×行的小時數(shù)＝一共行的路程

（2）專用的數(shù)量關(guān)系。

專用的數(shù)量關(guān)系就是從若干個具體數(shù)量關(guān)系式中概括出專用數(shù)量關(guān)系式。

如“單價×數(shù)量＝總價”，它是多個相關(guān)的數(shù)量關(guān)系概括得到的，每件衣服價格×件數(shù)＝衣服總價，每個籃球的價格×個數(shù)＝籃球總價，每張桌子的價格×張數(shù)＝桌子總價，等等，從而來概括單價、數(shù)量和總價這3個專用名詞，形成一個專用的數(shù)量關(guān)系。再如，“速度×?xí)r間＝路程”，“工作效率×?xí)r間＝工作總量”，也是如此。

（3）抽象的數(shù)量關(guān)系。

抽象的數(shù)量關(guān)系是指在運用數(shù)量關(guān)系的過程中高度概括得到的。在小學(xué)階段，可以概括成最基本的四個：部分?jǐn)?shù)與總數(shù)的關(guān)系；兩個數(shù)相差關(guān)系；每份數(shù)、份數(shù)與總數(shù)的關(guān)系；兩個數(shù)的倍數(shù)關(guān)系。

2.理解數(shù)量關(guān)系的數(shù)學(xué)本質(zhì)。

理解數(shù)量關(guān)系，解決數(shù)學(xué)問題的過程就是從現(xiàn)實生活中或具體情境中抽象出數(shù)學(xué)問題，利用數(shù)學(xué)符號表示數(shù)學(xué)問題中的數(shù)量關(guān)系和變化規(guī)律，求出結(jié)果并討論結(jié)果。本課中，行程問題的數(shù)量關(guān)系教學(xué)，不僅要讓學(xué)生理解關(guān)系的意義，利用數(shù)量關(guān)系解答相關(guān)的題目，還為學(xué)生的后續(xù)學(xué)習(xí)，即正反比例的學(xué)習(xí)，起到了一個滲透的作用。

（1）理解算式關(guān)系的價值。

在“課程內(nèi)容”的第二學(xué)段“數(shù)的運算”的第7條明確指出：“在具體的情境中，了解常見的數(shù)量關(guān)系：總價=單價×數(shù)量、路程=速度×?xí)r間，并能解決簡單的實際問題。”

學(xué)生在解決以下兩個問題的時候，主要讓學(xué)生明白：

算式與數(shù)量關(guān)系是相對應(yīng)的；

已知（ ）和（ ），求（ ），可以運用怎樣的數(shù)量關(guān)系來求。

（2）函數(shù)關(guān)系的價值。

我們經(jīng)常看到，在六年級學(xué)習(xí)“正反比例”的時候，學(xué)生理解起來比較麻煩，學(xué)生很難弄清楚正反比例的關(guān)系。其實正反比例關(guān)系就是數(shù)量之間的變化關(guān)系，在這里可以讓學(xué)生體會和感受到，路程不變，乘坐不同的交通工具，時間是不一樣的，速度變了，時間也會變；速度不變，行的時間越長，行的路程就越多。

想一想，填一填。

速度（千米/時）時間（小時） 路程（千米） 數(shù)量關(guān)系①20 2 40②20 4 80③20 8 160

仔細(xì)觀察第一張表格，我發(fā)現(xiàn)：

3.理順數(shù)量關(guān)系的教學(xué)思路。

縱觀以上的分析與思考，對于這節(jié)課有了系統(tǒng)的思考和整體的把握。可以把這節(jié)課的教學(xué)目標(biāo)設(shè)定為：使學(xué)生通過具體的生活事例理解概括“速度、時間、路程”的實際含義；理解“速度、時間、路程”之間的數(shù)量關(guān)系，滲透函數(shù)思想；初步培養(yǎng)學(xué)生運用數(shù)學(xué)語言表達(dá)數(shù)量關(guān)系的能力，并能靈活運用數(shù)量關(guān)系解決實際問題；提高對數(shù)學(xué)學(xué)習(xí)的興趣。

（1）自主抽象數(shù)量關(guān)系，認(rèn)識數(shù)量關(guān)系表述的層次性。

數(shù)量關(guān)系的表達(dá)，在不同的年段有著不同的要求，在低段要求學(xué)會用具體的數(shù)量關(guān)系式來表達(dá)，幫助學(xué)生理解題目的意思，到了中高段要求學(xué)生學(xué)會專用的數(shù)量關(guān)系，建立起題型結(jié)構(gòu)。

①抽象出專用數(shù)量關(guān)系。

學(xué)生通過數(shù)量關(guān)系的前測作業(yè)，可以敘述具體的數(shù)量關(guān)系表達(dá)式，在理解了具體的數(shù)量關(guān)系后，讓學(xué)生抽象出行程問題中專用的數(shù)量名詞，速度、時間和路程，可以讓學(xué)生感受到專用的數(shù)量關(guān)系比較簡潔和貼切，體現(xiàn)數(shù)學(xué)學(xué)習(xí)的簡潔性。

②突破“速度”這一難點。

這里對學(xué)生來說，“速度”的概念比較抽象，不像路程那么明確，不像時間那么常見，并且速度的單位是由兩部分組成的，它的表示形式學(xué)生從未見過。因此，教學(xué)關(guān)鍵是讓學(xué)生從大量的生活實例中感知并理解速度的含義。通過計算自行車、飛機(jī)、宇宙飛船的平均速度，讓學(xué)生比較“千米 /小時”、“千米 /分”、“千米 /秒”三個單位，自主小結(jié)出“速度表示每小時、每分鐘、每秒鐘行走的千米數(shù)”。再以汽車儀表盤上時速表，發(fā)現(xiàn)“km/h”這一速度單位，感受“速度”在我們實際生活中的應(yīng)用。

（2）創(chuàng)設(shè)教學(xué)問題情境，理解數(shù)量關(guān)系內(nèi)涵的多元性。

解決問題的教學(xué)，離不開情境，通過情境，可以幫助學(xué)生理解數(shù)量關(guān)系，解決實際問題，從而體現(xiàn)數(shù)量關(guān)系的價值。

①體現(xiàn)算式關(guān)系。

這是剛才數(shù)量關(guān)系的一個簡單變式，求速度和求時間的問題。通過前面的學(xué)習(xí)，學(xué)生對行程問題的題目已經(jīng)有了一個結(jié)構(gòu)化的認(rèn)識，它有速度、時間、路程三個要素構(gòu)成。已知“速度×?xí)r間＝路程”，根據(jù)算式關(guān)系，學(xué)生可以推導(dǎo)出“速度=路程÷時間，時間=路程÷速度”。教學(xué)時，要重視幫助學(xué)生分清條件和問題，熟悉數(shù)量關(guān)系，建立“問題—條件—算法”之間的聯(lián)系系統(tǒng)，即要求（ ），必須要知道（ ）和（ ）這兩個條件。

②體現(xiàn)函數(shù)關(guān)系。

問題情境：小明從家到學(xué)校有1500米，采用兩種不同的方式。一種是走著去，一種是騎自行車去。哪種方式會快一些？

這里初步讓學(xué)生感受到，路程不變的情況下，速度快了，時間就少了，速度慢了，時間就多了。

再者可以讓學(xué)生體驗一下，哪個圖表示的是走路，哪個圖表示的是騎車？滲透統(tǒng)計圖的知識來領(lǐng)悟路程與時間的關(guān)系。(如下圖)

再是利用“題組”的訓(xùn)練形式，領(lǐng)悟數(shù)量之間的變化情況，在理解它們之間的變化情況的同時，聯(lián)系“積的變化規(guī)律”，進(jìn)一步加強(qiáng)對學(xué)生數(shù)感的培養(yǎng)。

想一想，填一填。

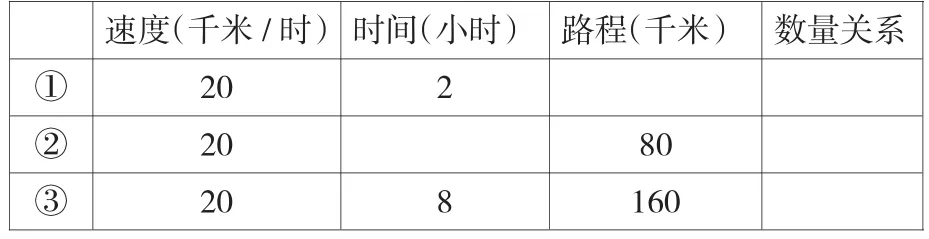
速度（千米/時）時間（小時） 路程（千米） 數(shù)量關(guān)系① 20 2② 20 80③20 8 160

仔細(xì)觀察這張表格，我發(fā)現(xiàn)：

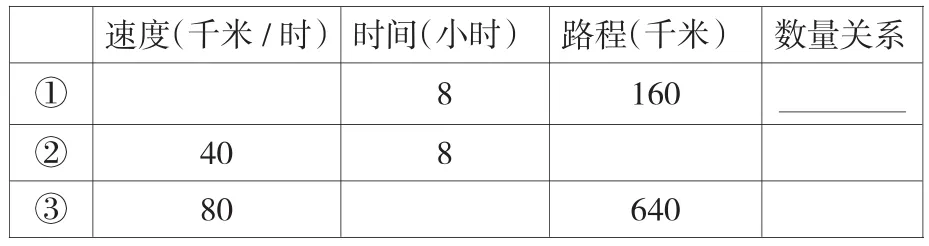
速度（千米/時）時間（小時） 路程（千米） 數(shù)量關(guān)系①8 160②40 8③80 640

仔細(xì)觀察這張表格，我發(fā)現(xiàn)：___________

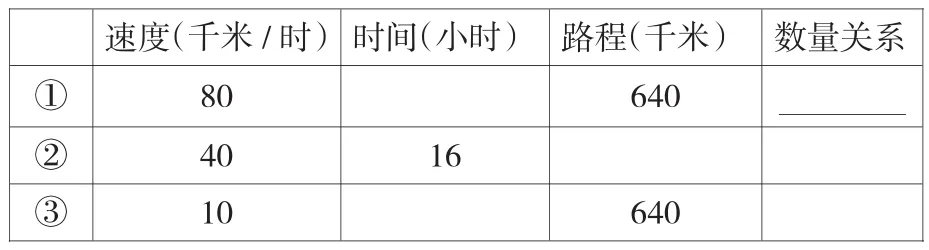
速度（千米/時）時間（小時） 路程（千米） 數(shù)量關(guān)系① 80 640②40 16③10 640

仔細(xì)觀察第一張表格，我發(fā)現(xiàn)：___________

（3）創(chuàng)設(shè)現(xiàn)實問題情境，感受數(shù)量關(guān)系應(yīng)用的靈活性。

數(shù)學(xué)的價值在于使學(xué)生學(xué)會運用所學(xué)的知識去分析、解決生活中的問題，關(guān)鍵在實踐運用。生活中有著豐富的數(shù)學(xué)資源，它們都是學(xué)生實踐運用的最佳素材。

①總結(jié)行程問題中的數(shù)量關(guān)系：

②舉一反三：這種“一乘二除”的形式：

單價×數(shù)量=總價

每盤蘋果數(shù)×盤數(shù)=蘋果總數(shù)

每張課桌的價格×課桌的數(shù)量=課桌的總價

……

③構(gòu)建出數(shù)學(xué)模型：

從行程問題的基本數(shù)量關(guān)系拓展到“單價×數(shù)量=總價”、“每盤蘋果數(shù)×盤數(shù)=蘋果總數(shù)”等，從而歸納出“每份數(shù)”、“份數(shù)”和“總數(shù)”之間的關(guān)系，引導(dǎo)學(xué)生在實踐應(yīng)用中構(gòu)建了數(shù)學(xué)模型。從具體到抽象，促進(jìn)了學(xué)生思維的發(fā)展和知識體系的完善。