探尋運算定律背后的意蘊

陳泰昌

[摘 要]對于運算定律的教學，其中的乘法分配律是學生最難理解和掌握的，因為學生常常將乘法分配律與乘法結合律混為一談，導致錯誤百出。分析發現，主要有兩個方面的原因：一是對運算定律的結構特征認識模糊；二是對運算定律的數據特征缺乏關注。因此，教師在教學中要積極探尋運算定律背后的意蘊，引導學生準確把握乘法分配律的本質內涵。

[關鍵詞]運算定律 乘法分配律 結構特征 數據特征 意蘊 乘法結合律 本質內涵

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）11-017

四年級下冊第三單元是運算定律的教學，在這一單元中重點學習加法的交換律、結合律和乘法的交換律、結合律、分配律這五條運算定律。在小學階段，這五條運算定律不僅適用于整數的加法和乘法，而且適用于小數、分數的加法和乘法，所以在整個小學階段占有重要的地位和作用。當然，隨著數的范圍的進一步擴展，這幾條運算定律在有理數、實數甚至復數中仍然成立。所以，它們被譽為“數學大廈的基石”，對數學教學有著重要的意義和作用。

錯 題 羅 列

這么重要的運算定律，學生掌握與運用起來卻不是那么容易的事，尤其是乘法分配律。教學實踐中，我們發現學生在學習乘法分配律后，腦子就亂成一鍋粥，如遇“括號”就“分配”、遇“分配”就“相加”等，已經分不清什么是乘法交換律、什么是乘法結合律了。學生的錯題猶如“忽如一夜春風來，千樹萬樹梨花開”，讓我們飽受煎熬。下面，讓我們來看看學生千奇百怪的錯題。

透過學生的錯題，我們不難發現，學生錯題的最大特點就是將乘法分配律與乘法結合律混為一談。當然，相對于其他幾條運算定律，乘法分配律較乘法交換律和乘法結合律的組成要素多，展開算式的步驟要多，還出現加法和乘法兩三步混合運算。這種分分合合、合合分分的變式，學生最容易混淆運算定律。

教 學 嘗 試

為什么學生應用運算定律進行計算會感到如此困難？究其原因，主要有以下兩個方面：一是對運算定律的結構特征認識模糊；二是對運算定律的數據特征缺乏關注。那么，如何在教學中讓學生對運算定律有清晰的整理和有條理的厘清呢？筆者經過一段時間的思考后，對“乘法分配律”一課的教學進行如下設計。

一、鋪設情境，發現規律的結構特征

1.出示情境

（1）學校購買春裝校服，每件上衣30元，每條褲子25元，買這樣的40套衣服一共要多少元？（只列式不計算）

方法①：（30+25）×40 方法②：30×40+25×40

（組織學生交流，分別說說這兩種方法的解題思路）

（2）在一長方形花圃里栽郁金香和菊花（如下圖），這個花圃占地多少平方米？（只列式不計算）

方法①：（45+26）×15 方法②：45×15+26×15

（組織學生交流，分別說說這兩種方法的解題思路）

2.引導聯想

師：像這樣可以用兩種方法解決的實際問題還有很多，你能舉一些例子嗎？

（出示例題，只列式不計算）

……

【設計意圖：課伊始，無論是情境創設中的例題，還是師生列舉的問題，都要求學生只列式不計算，目的是讓學生在列式過程中體會兩種計算方法：一種方法是“先求和，再相乘”；另一種方法是“先分別乘，再求和”。但無論是“先求和，再相乘”的方法，還是“先分別乘，再求和”的方法，都是這種類型應用題的結構特征，而且在數據的安排上也沒有特意出現湊整。】

3.引導觀察

（1）解決相等關系。

師：觀察左右兩邊的算式，你覺得它們都相等嗎？分別選一題的兩道算式算出得數，看看這兩道算式的得數是否相等。

（2）用符號分別表示出兩種算式的結構特點，如（□+□）×□，□×□+□×□。

（3）你能舉這樣兩個相等的算式嗎？試試看。

討論：這里，具有兩種結構的算式具有怎樣的大小關系？

生：相等。

（師用“=”連接）

（4）師列舉錯誤的例子，如（102+200）×35=102×35+35等。

學生討論比較后得出：僅僅具有這樣的結構特征還不能說明兩個算式相等，還必須要關注數據是否也符合一定的特征。

……

【設計意圖：解決相等的問題，由結構形似引出結構特征，更多的是結合學生已有的經驗，引導學生從具體數據的討論上升到規律的發現與歸納，最終構建相應的數學模型。】

二、深入探究，發現規律的數據特征

1.研究數據中存在的規律

（1）提問：相等的算式中，數據應該具備怎樣的特征呢？

提示：等號左邊是三個數，等號右邊卻變成四個數了，怎么變的？

（2）提問：是不是只要具備這樣的結構特征，又具備這樣的數據特征，兩個算式就一定相等呢？（生舉例略）

（3）討論交流。

學生得出：如果具備這樣的結構特征，又具備這樣的數據特征，那么兩個算式就一定會相等。

2.研究規律的合理性

師：這樣的現象是巧合，還是客觀存在的事實？你能用學到的知識去解釋這樣的現象嗎？

（引導學生用乘法的意義去解釋現象存在的科學性，并舉例說明）

3.抽象概括乘法分配律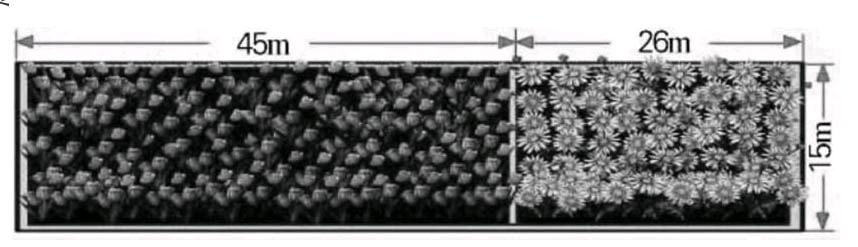

師：看來，這是一個普遍存在的規律，你能用一個式子表示出這一規律嗎？

（讓學生表示這一規律并說說所表示的規律是否具有結構特征，同時也具備數據特征）

師：這樣說太麻煩了，可以用什么來表示出字母形式？

4.揭題

師：這就是我們這節課研究的一個新的定律，叫做乘法分配律。請你用自己的話說說對乘法分配律的理解。

……

【設計意圖：探究數據中存在的規律，讓學生從原理上理解不同算法間存在的意義。在乘法分配律的學習中，無論是從（a+b）×c到a×c+b×c的分解式思考，還是從a×c+b×c到（a+b）×c的合并式思考，都可以結合乘法的意義來理解，讓學生“不僅知其然，而且知其所以然”。】

三、鞏固應用，拓展規律

（1）根據乘法分配律，請你說說和下列算式相等的算式。

（42+35）×2 72×（30+6） 18×52+48×18

（2）橫著看，在得數相同的兩個算式后面畫“√”。

（28+16）×7 = 28×7+16×7………………（ ）

56×（19+28）=56×19+28…………………（ ）

（3）看一看、比一比，每組算式中哪一題的計算比較簡單。為什么這樣選，你從中有什么啟發？

① 64×8+36×8 ② （25+250）×4

（64+36）×8 25×4+250×4

③ 99×76+76 ④ 125×（80+2）

（99+1）×76 125×80+125×2

【設計意圖：這些問題的設計，給學生的自主探究提供了機會，讓他們聯系已知，應用已學的方法去探索，培養了學生由此及彼的推理能力，讓他們經歷了知識的發生、發展過程。】

實 踐 感 悟

實踐表明，這樣設計教學，使學生對乘法分配律的認識清晰且深刻，能在后續的計算練習中駕輕就熟、應用自如。這一成功案例，引起筆者對運算律教學的諸多思考。

感悟1：結構模型優于數據特點

運算定律的學習，更多的是讓學生對已有的知識和經驗進行積累，使學生從具體數據的討論上升到規律的發現與歸納，最終構建相應的數學模型。然而，我們許多教師在教學運算定律時，都喜歡把注意力聚焦在數據的特點上，從數據的特點入手，引導學生在特殊的數據中發現其特有的規律。如加法交換律、乘法交換律，學生首先發現的是數據沒有變，只是數的位置發生了變化；又如加法結合律、乘法結合律也是數據不變，括號的位置發生了變化。對數據的片面關注，使得學生在一開始接觸運算定律時就將目光放在了數據的特點上，而對算式的結構缺乏研究，導致學生對乘法結合律與乘法分配律混淆不清，因為學生只看到數據而沒看到算式結構的特點。雖說數據特殊于運算定律非常重要，但結構特殊更是不容忽視。結構猶如房屋框架，框架沒有搭建則房屋難以成形。對結構認識模糊，規律的認識不可能清晰，運算定律的模型就無法構建。

從注意力的角度看，結構相比數據較為隱蔽，不容易引起學生的重視。這就需要教師有意識地給予引導，并以此入手，引起學生足夠的關注。如筆者在設計本課教學時就從結構入手，通過列式解決問題，引導學生發現每一個問題都有兩種解題思路，這兩種思路的算式表達都是“先求和，再相乘”或“先分別乘，再相加”，在此基礎上引出算式結構的知識，將學生的注意力引向對算式結構的觀察。繼而，要求學生聯系平時所學，解決相應的實際問題，幫助學生進一步鞏固對乘法分配律的認識。

從結構入手，強化了學生的結構意識，使他們對乘法分配律的結構印象深刻。在學生清晰結構的基礎上，筆者再設問：“是不是只要符合這樣的結構特征，算式就一定相等呢？”……這里，筆者認為用乘法分配律進行描述，更能讓算式結構深入學生腦海之中。

因此，從結構入手應該成為運算定律教學的一種思路，無論是首次接觸的加法交換律、結合律，還是后來學習的乘法交換律、結合律，盡管結構單一，但還是有必要讓學生先在結構上觀察，再從數據上研究。

感悟2：運算意義是運算定律的依據

在運算定律的教學中，教師采用的都是不完全歸納法，即引導學生通過多個算式發現其中存在的共同規律，繼而用字母表示出各個運算定律的表達式。用這樣的方式進行教學本無可厚非，然而筆者總覺得缺少了些什么，那就是給找到的規律尋找可解釋的依據。

運算定律是對數的運算過程中基本規律的歸納與總結，因此學生理解運算定律的內涵，離不開運算意義的支持。如理解加法交換律時，教師應引導學生始終把握“加法是把兩個數合并成一個數的運算”這一本質內涵。而乘法交換律為乘數位置交換積不變，其理由也可以從乘法的表達方式去解釋。如“6個15相加的和是多少”，用算式表示可以是6×15，也可以是15×6。加法結合律和乘法結合律同樣可以從運算意義的角度去理解為變化運算順序后結果相等，而乘法分配律“先求和，再相乘”與“分別乘，再相加”的結果相等，即無論是從（a+b）×c到a×c+b×c的分解式思考，還是從a×c+b×c到（a+b）×c的合并式思考，都可以結合乘法的意義來理解，都是求相同加數的和的簡便運算。如45×15+26×15與（45+26）×15，前者表示45個15與26個15的和是多少，后者表示45加26等于71，71個15的和是多少。所以，從運算意義上去理解運算定律，更有助于培養學生合理選擇算法的能力，發展他們思維的靈活性。

所以，教師在教學中應結合具體的內容，引導學生體會數學的思維方式和嚴謹求實的科學態度，這既是數學教學的重要目標之一，又是提高學生數學素養的良好途徑。同時，這也是幫助學生理解規律的重要舉措，是對不完全歸納法的一種補充。

感悟3：把握運算定律與簡便計算的聯系和區別

運算定律是一種模型化知識，簡便計算則是根據算式和數的特點，依據四則運算的性質，在不改變運算結果的前提下靈活處理運算程序，以達到簡便易算的目的。這兩者既有著緊密的聯系，又有一定的區別。教學中，因為運算定律是運算本身固有的性質，也是后續代數知識學習的必備基礎，因此不能簡單地等同于簡便計算教學，但運算定律的學習過程，也是為后續靈活計算積累相應的活動經驗的過程。因此，教師在教學中可以將過程延長，使內容豐富些、形式多樣些，并注意讓學生探究、嘗試、交流、質疑，在引導學生理解和掌握運算定律的同時，培養和發展學生思維的靈活性。

感悟4：后續教學注重變式分類

如前面提到，無論是運算定律還是簡便計算，在后續學習中還要安排專門的課時進行訓練。所以，在這一環節中需要對乘法分配律進行全面的變式練習，學生只有清晰地把握這些變式的類型，才能靈活應用乘法分配律解決問題。如延展乘法分配律項數的變式，將兩數和與一個數相乘變為三四個數的和與一個數相乘，即（a+b+c）×d=a×d+b×d+c×d；將兩個數的和變為兩個數差的變式，即（a-b）×c=a×c-b×c；將特殊數1參與展開的變化式，即（a+1）×b=a×b+b×1。

綜上所述，對于運算定律的教學，尤其對于棘手的乘法分配律的教學，只有探尋定律背后的意蘊，學生才能真正掌握乘法分配律的本質內涵，在簡便計算以及解決問題時才能“以不變應萬變”。只有如此，“數學大廈基石”才會夯實，才會堅固！

（責編 藍 天）