淺談高中數學例題解析

?

淺談高中數學例題解析

◇甘肅劉克庭

當前,我國正在推廣新課程的改革,不但包含了改革課程的內容設立,還包括了改革教師的教學觀念、教學方式,只有這樣才有助于完成我國的教育體度改革的最終目的．教學中例題教學方式的選擇在提升高中數學課堂教學質量、完成教學目的方面發揮了關鍵的作用．鑒于此,本文擬對高中數學例題解析進行分析與探究．

1例題解析存在的問題

高中數學課程在內容設立層面是相對落后,同時在例題的選取上相對單一，例題的數量比重較大,導致課堂教學目的不容易完成．因為高中數學公式、定理的應用方法通常有很多種,若逐一講解,就會滯后課程的進程,進而無法實現預期目的．

教師講解例題時耗費的時間太多,同時講解得過分詳細了,阻礙了學生自主學習與自主探究能力的提升．在整個教學過程中教師忽視了學生的主體位置,只是自己在一味地解說,學生沒有考慮與綜合的機會,這樣會顯著地降低高中數學課堂的教學效率,阻礙完成教學改革的目的．在這類情況之下,學生的積極性會被慢慢地打消,長期下去學生就會失去自主學習與單獨思考的能力,在自己單獨解決題目的時候效率就會顯著下降．

2例題解析的注重點

2.1教學方式靈活變通培育學生的思維習慣

著名數學家費賴登塔爾曾經說過：“學習數學唯一科學的方式就是‘再創造’，也就是通過學生本人將要學的東西去發現與創造出來,而教師的重要任務是去指引與協助學生去完成這個再創造性工作，而不是將現有的知識傳輸給學生．”所以教師在講解例題時，不要局限于某一類的教學方式與解題思維，更不必把思考經過直接告訴學生,而是要從不同角度去思索例題的解法,從而開闊學生的解題思路．這就需要教師在講解例題的時候,正確應用小組協作、自探互教等教學方法鼓舞學生自主地去找到新思路、找到新解法，進而培育學生正確的思維方式．另外還需要培育學生反思例題的習慣，利用在例題的思考中完成反思識別解題思路是否嚴謹、解題方法的多樣性,并且嘗試總結處理這類問題的普遍規律．

2.2重視思維指引，正確講解例題

在課堂教學中，應利用教師與學生、學生與學生的互動與協作，按照教學規律正確地把例題探究的思考經過說明白、講徹底，讓學生知道數學思維形成的經過．高效率的數學學習不但需要借助效仿跟記憶,還要指引學生自覺參加到觀察、思索、推斷、驗證與溝通等思維行為中，幫助學生構成自己對數學知識的認知與了解.教師的首要工作就是教會學生去探究、處理問題的想法與方式．

2.3深層探究教材，開發例題的潛在意義

我國著名教育學家葉圣陶先生曾說過：“教材只能作為教課的依據.要使學生真正受到實益主要依據老師在課堂上的運用能力．”教師要深層次地探究所教的知識與所選用例題相互的關聯并設定相應的情境，挖掘例題潛在的德育價值，使得學生能夠進入到良好的數學情感與人文關懷之中.這不僅能夠培育學生對數學學科的感情，還可以潛移默化地改變學生的價值觀念．

2.4注重學生能力的擴展

數學例題教學不僅需要學生了解數學的基本知識與技能，其更多的是需要利用例題教學擴展學生的能力.一題多變可以激起學生濃厚的求知渴望，增加學生對課堂所學內容的深刻認識.

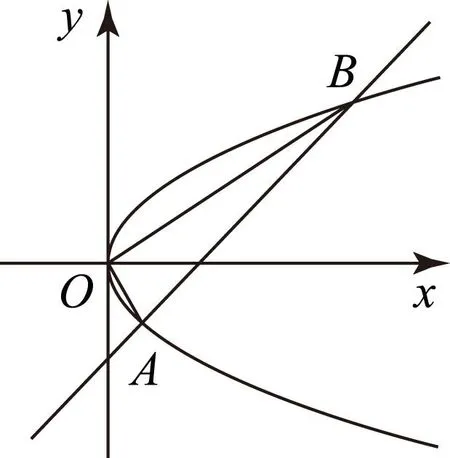
圖1

在此題基礎上可引導學生進行如下探究:

1) 逆向探究:設點A和B為拋物線y2=2x上原點以外的2個動點,已知OA⊥OB,則直線AB恒過定點Q(2,0).

2) 推廣一般:直線AB過Q(2p,0),交拋物線y2=2px(p>0)于A、B,O是坐標原點,則OA⊥OB.

3) 逆向推廣:設點A和B為拋物線y2=2px(p>0)上原點以外的2個動點,已知OA⊥OB,則直線AB恒過Q(2p,0).

3例題解析的實例探討

通過老師的正確指引后，學生自己思考,給出了如下多種變式.

變式1:A={x|x<1},B={x|x≤m},A?B,求m的取值范圍．

變式2:A={x|x<1},B={x|x>m},A?RB,求m的取值范圍．

變式3:A={x|-1

變式4:A={x|-1

變式5:A={x|-1

其中變式1與2本質是一樣的．變式3與前2題相比，難度增加了.變式4與變式3不同之處是這里的B可以為?,而在變式5里,能夠判斷出B不可能是?．通過這5道變式的訓練，不僅可以讓學生加強了解集合的包含關聯,還可以加深解題的想法.通過分析子集是空集的狀況,培育了學生思考的嚴謹性.

在教師的指引下，學生通過自己思考,給出了多種解法:

思考1如果將x+y看成是一個變量,問題就變成想辦法去掉xy項．

思考2利用構建方程來進行處理.

解法2令t=x+y>0,所以y=t-x,代入條件可得x2-tx+2-t=0.由Δ=t2-4(2-t)≥0,解得

思考3條件等式能夠完成因式分解,應用積為定值,和有最小值來求解．

解法3由x+y+xy=2可知

(x+1)(y+1)=3,

總之，例題教學是一項較為系統的工作,不能一蹴而就,需要從多方面完善,靈活變通教學方法，進而培育學生的思維方式．

(作者單位：甘肅省景泰縣第五中學)