函數零點問題的求解策略

?

函數零點問題的求解策略

◇甘肅蔡鵬

函數零點，即當y=0時，對應的x值.零點不是點，而是數值.高考對函數零點的考查，主要包括零點個數或零點分布.本文將介紹幾種零點問題的求解策略.

1數形結合法

A1;B2;C3;D4

圖1

由圖1可知,2個函數的交點個數為2,所以函數f(x)=2x|log0.5x|-1的零點個數為2．故選B.

變式已知函數f(x)=|x-3|+1,g(x)=ax.若方程f(x)=g(x)有2個不相等的實根,則實數a的取值范圍是________.

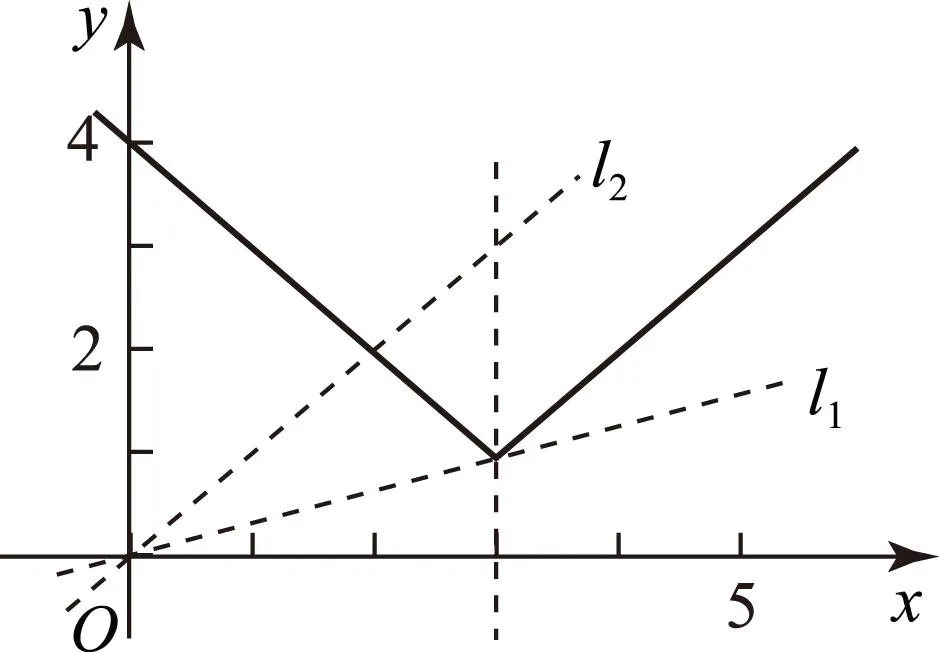
圖2

由圖可知g(x)=ax的圖象從l1的位置轉到l2時,方程f(x)=g(x)有2個不相等的實根,g(x)在l1時a=1/3,g(x)在l2時a=1, 故a的取值范圍是1/3

2二分法

A(a,b)和(b,c);

B(-∞,a)和(a,b);

C(b,c)和(c,+∞);

D(-∞,a)和(c,+∞)

由于a0,

f(b)=(b-c)(b-a)<0,

f(c)=(c-a)(c-b)>0．

因此有f(a)·f(b)<0,f(b)·f(c)<0.又因為f(x)是關于x的二次函數,函數的圖象是連續不斷的曲線,因此函數f(x)的2個零點分別位于區間(a,b)和(b,c)內．

變式函數f(x)=log2x-1/x的零點所在的區間是().

A(0,1/2);B(1/2,1);

C(1,2);D(2,3)

3導數法

A (-14,0); B (0,14);

f(0)=e0+4×0-3=-2<0,

方法2此題可先將2個函數分離,再借助于數形結合的方法進行求解．可以令g(x)=ex,h(x)=-4x+3．畫出2個函數在同一坐標系中的圖象如圖3.根據2個函數的圖象的交點所在的區間即可獲解．

圖3

變式已知函數f(x)=lnx-x+2有一個零點所在區間為(k,k+1) (k∈N*),則k的值為____．

函數與方程的考查內容除了零點所在的區間和根的個數問題以外,函數零點的應用也是常見的題型.在應用上述幾種策略解題時，若直接求解很難奏效,可將條件轉化后再利用其求解.

(作者單位：甘肅省張掖市實驗中學)