廣義鞍點問題的塊對角預條件子

何 軍，劉衍民

（遵義師范學院數學與計算科學學院，貴州遵義,563002）

自然科學研究

廣義鞍點問題的塊對角預條件子

何 軍，劉衍民

（遵義師范學院數學與計算科學學院，貴州遵義,563002）

研究了廣義鞍點問題新的塊預條件子，給出了預處理后矩陣特征值的一些性質.數值例子表明，新的預條件子是非常有效的.

預處理；鞍點問題；特征值

考慮如下的鞍點系統：

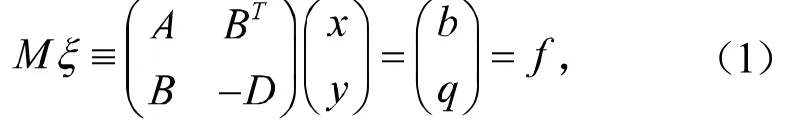
在文獻[1]中，Benzi、Golub和Liesen討論了解決鞍點系統的一系列的數值方法，并且給出了一些預條件子來解決系統（1），如：塊對角預條件子[2-8]，塊三角預條件子[9,10]，HSS類型的預條件子[1,11,12].

其中 .可以發現，當D=0，文獻[4,7,8]中介紹了非確定的塊對角預條件子.

基于上面的分析,本文主要研究下面的正定的塊對角預條件子：

1主要結果

考慮如下的預條件子：

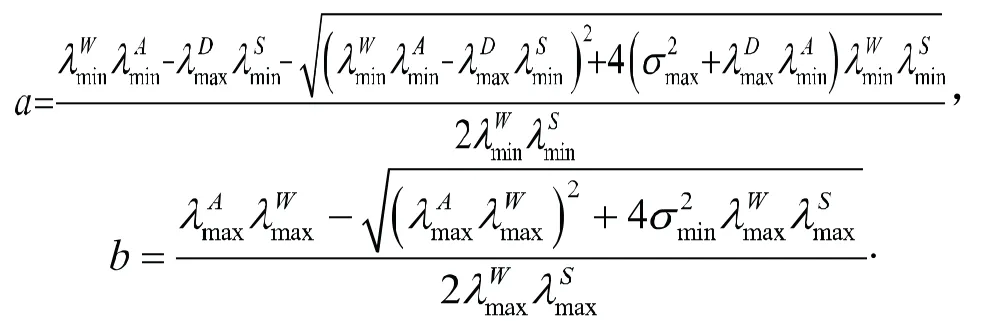
展開（2）式有：

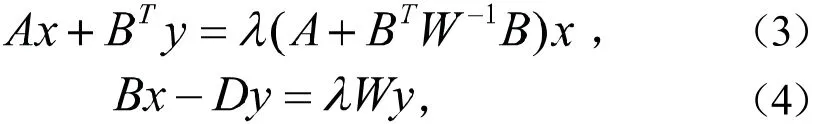
帶入（4）式可得：

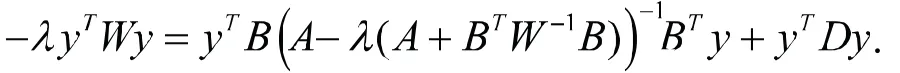
那么可得：

直接計算可得：

因為

有：

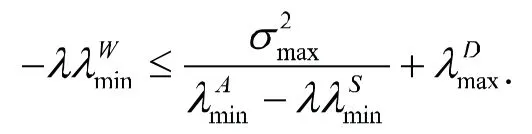
直接計算可得：

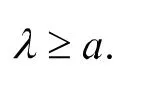
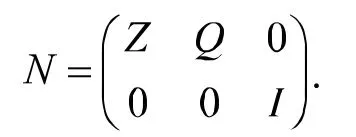
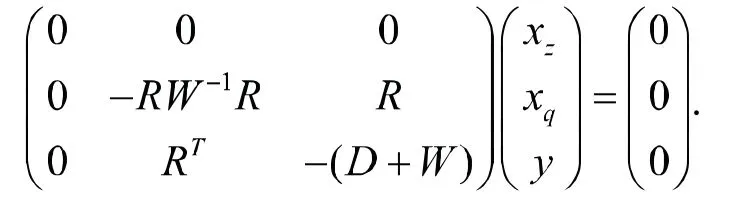
證明完畢.

注：所有的預處理后的矩陣的特征值都包含在兩個狹窄的區間中，并且可以發現其中的一些界可以用文獻[14]中的定理2.1來表示矩陣的界.但是，至少其中的一個界表現得更好，如正特征值的上界.

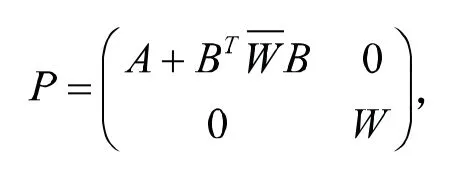
2 數值例子

考慮下面的Stokes類型問題：

如果用穩定有限元或者有限差分方法來離散上面的問題，可以得到廣義的鞍點線性系統.本文用Silvester、Elman和Ramage編寫的IFISS軟件包[15]來離散系統，所采用的混合有限元是雙線性速度一常數壓力： 對有限元，得到系數矩陣的(1,1)塊的矩陣是對稱正定的，(1,2)塊的矩陣是滿秩的.例子中用32×32的網格來離散系統（也就是說，D≠0，且穩定系數為 =0.25），其中表示矩陣中非零元的個數.

表1 相關矩陣的規模及非零元的個數

表2 對不同的W,MINRES迭代的迭代步數

圖1 當W=0.1I，對于32×32網絡預處理后的矩陣P-1A的特征值分布情況

圖2 當W=2diag(BBT)，對于32×32網絡預處理后的矩陣P-1A的特征值分布情況

圖3 對不同的W，32×32網絡MINRES迭代的迭代曲線及步數

表1描述了不同網格鞍點問題的規模和稀疏情況，表2給出了不同矩陣WMINRES子空間迭代的迭代步數.

[1]M Benzi,G H Golub,J Liesen.Numerical solution of saddle point problems[J].Acta Numerica,2005,(14):1-137.

[2]E de Sturler,J Liesen.Block-diagonal and constraint preconditioners for nonsymmetric indefinite linear systems,part I:Theory[J].SIAM J Sci Comput,2005,(26):1598-1619.

[3]C Siefert,E de Sturler.Preconditioners for generalized saddlepointproblems[J].SIAMJ Numer Anal,2006,44(3):1275-1296.

[4]T Rees,C Greif.A preconditioner for linear systems arising frominterior pointoptimization methods[J].SIAM J Sci Comput,2007,(29):1992-2007.

[5]G H Golub,C Greif,James M Varah.An algebraig analysis of a block diagonal preconditioner for saddle point sysytems[J]. SIAM J Sci Comput,2006,(27):779-792.

[6]M F Murphy,G H Golub,A J Wathen.A note on preconditioning for indefinite linear systems[J].SIAM J Sci Comput, 2000,(21):1969-1972.

[7]C Greif,D Schotzau.Preconditioners for saddle point linear systems with highly singular(1,1)blocks[J].Electron Trans Numer Anal,2006,(22):114-121.

[8]C Greif,D Schotzau.Preconditioners for the discretized timeharmonic Maxwell equations in mixed form[J].Numerical Linear Algebra Appl,2007,(14):281-297.

[9]A Klawonn.Block-triangular preconditioners for saddle point problems with a penalty term[J].SIAM J Sci Comput,1998, (19):172-184.

[10]Z H Cao.Augmentation block preconditioners for saddle point-type matrices for singular(1,1)blocks[J].Numerical Linear Algebra Appl,2008,(15):515-533.

[11]Z Z Bai,G H Golub,M K Ng.Hermitian and skew-hermitian splitting methods for non-hermitian positive definite linear systems[J].SIAM J Matrix Anal Appl,2003,(24):603-626.

[12]V Simoncini,M Benzi.Spectral properties of the hermitian and skew-hermitian splitting preconditioner for saddle point problems[J].SIAM J Matrix Anal Appl,2004,(26):377-389.

[13]Ilse C F Ipsen.A note on preconditioning nonsymmetric matrices[J].SIAM J Sci Comput,2001,(23):1050-1051.

[14]D Silvester,A Wathen.Fast iterative solution of stabilized Stokes systems part II:using generalblock preconditioners[J]. SIAM J Numer Anal,1994,(31):1352-1367.

[15]H Elman,G H Golub.Inexact and preconditioned Uzawa algorithms for saddle point problems[J].SIAM J Numer Anal, 1994,(31):1645-1661.

（責任編輯：朱 彬）

Block Diagonal Pre-conditioners for Generalized Saddle Point Problems

HE Jun，LIU Yan-min
(School of Mathematics and Computer Science,Zunyi Normal College,Zunyi 563002,China)

In this paper,we consider block diagonal preconditioners for solving saddle point linear systems;we show properties of eigenvalues of the preconditioned matrix.Finally,numerical experiments are also reported for illustrating the efficiency of the presented preconditioners.

saddle point system;preconditioning;eigenvalue

O211.4

A

1009-3583（2016）-0111-03

2016-05-11

國家自然科學基金資助項目（71461027）；貴州省科學技術基金（黔科合基礎[2016]1161）；遵義師范學院博士基金資助項目（遵師BS[2015]09）

何 軍，男，四川資陽人，遵義師范學院數學與計算科學學院教師，博士，主要從事數值代數的研究。