交互式多屬性群決策評價方法研究

杜 娟，霍佳震

(同濟大學經濟與管理學院，上海 200092)

交互式多屬性群決策評價方法研究

杜 娟，霍佳震

(同濟大學經濟與管理學院，上海 200092)

針對多屬性群決策中屬性指標權重的確定，將群體看作由多個被評價且參與權重決策的獨立成員組成，提出一種交互式迭代算法，以均等屬性權重為起點進入迭代過程，每一次迭代在當前給定的權重參數下求解含參規劃模型并計算得到新的權重參數。迭代過程終止于任一群成員在相鄰兩次迭代的參數權重下加權綜合屬性值的絕對差異控制在非阿基米德無窮小量以內，此時使用的參數權重即為各屬性的最優權重。實際迭代計算過程以及屬性指標權重由所有群體成員共同參與和決定，故可以認為最終優化和選擇結果為絕大部分成員所接受并滿意。通過一個算例以及一個關于研發項目選擇的實例，說明該交互式群決策評價方法的可行性和有效性。

群決策；屬性權重；交互式迭代

1 引言

伴隨各個領域的現實決策問題日益復雜的趨勢，通過群體決策的方式進行決策分析的優勢越發得到認同與重視。多屬性群決策問題已然成為現代決策科學的重要組成部分，在社會、經濟、管理、軍事、工程等很多領域被廣泛運用。此類問題一般描述為多個專家就多個屬性或指標對一組候選成員進行比較并給出評價結果。目前對于多屬性群決策問題的研究主要集中于專家意見一致化與權重確定兩大方面。首先針對專家決策信息的一致化問題，由于各個專家的專業背景、知識結構、表達方式等不盡相同，所提供的代表評價結果的決策矩陣很可能存在較大差異，若直接進行意見集結，則可能出現個別極端值對最終結果的偏差影響。針對上述問題，很多學者從不同研究角度出發，提出一系列修正決策矩陣、實現合理一致的方法。例如，Bryson[1]指出一致化是一個動態迭代的群體決策過程，若專家之間的一致化程度未達到預先設定的一致化指標，則需要將個體決策信息返回給專家并討論修正，如此往復直至滿足一致化指標。Herrera-Viedma等[2]則著眼于不同偏好結構下群決策的一致化問題，提出使用個體決策信息與群體決策信息之間距離來度量一致化程度。徐澤水[3]研究了基于語言偏好關系的群決策問題，證明個體語言偏好關系與群體語言偏好關系之間的偏離度，不大于任意兩個體語言偏好關系間偏離度的最大值。王學軍和郭亞軍[4]采用G1-法進行個體決策結果的集結研究，避免了判斷矩陣的構建和一致性判斷。徐迎軍和李東[5]針對專家決策信息的一致化問題，提出群決策一致化迭代模型，利用乘性加權集結算子把方案的屬性值進行集結，從而自動完成個體意見一致化，無需專家多次修改決策信息。尤天慧等[6]針對具有不確定偏好序信息的多屬性群決策問題，提出將不確定偏好序轉換為投票數的計算公式，并依據Bernardo方法計算不確定偏好序信息對應的投票數并構建群體投票矩陣，由此進一步構造0-1整數規劃模型并根據求解結果得到方案排序結果。

其次，在群決策過程中，確定統一合理的權重，也是非常重要的研究方向，這里的權重既包括屬性指標的權重、也包括決策專家的權重。針對多屬性群決策中決策者的權重，國內外諸多學者進行了深入研究。早期研究或是通過決策者互相評分[7]、或是依據決策者的權威性及決策經驗[8]來確定權重，這種主觀權重對決策者彼此間的熟悉程度要求較高，很多實際場景并不適用。宋光興和鄒平[9]將決策者權重定義為主觀權重與客觀權重的凸組合，并分別給出基于層次分析法(Analytic Hierarchy Process，簡稱AHP)判斷矩陣和排序向量的確定客觀權重的幾種方法。后續研究重點圍繞決策者的客觀權重確定而展開，其中包括基于矩陣相容性指標和模糊聚類分析[10]、基于逼近理想解排序法(TOPSIS)[11-13]、綜合考慮內容權重和邏輯權重[14]等決策者賦權方法。隨著相關研究的不斷深入，很多文獻開始考慮區間模糊數的評價形式，例如Chen和Chau[15]提出基于專家模糊距離的隸屬度法；Chen Zhiping和Yang Wei[16]將各決策者的個體直覺模糊決策矩陣整合為群體直覺模糊決策矩陣，通過度量其接近度作為決策者權重的依據；Xu和Yager[17]提出一種新的相似度指標，并基于直覺模糊偏好關系將其運用于群決策的集成分析中；閆書麗等[18]將群體意見一致性與信息分布特點相結合，依據極大熵思想以及各決策者關于方案的綜合指標值與群體綜合指標均值間的灰色關聯度建立模型，由此確定各決策者權重。

關于屬性權重的研究，早期發展集中于主觀賦權法，即決策者依據經驗知識主觀判斷獲得，常用方法包括AHP法和Delphi法，方法雖然成熟但結果受主觀因素影響較大。后續研究開始關注客觀賦權法，即根據原始數據之間關系確定權重，從不同研究角度提出一系列方法。梁樑和王國華[19]提出一種基于多層次交互式決策模型的權重確定方法，由上級確定各指標權重的約束范圍和特定規則，各下級在上級約束下，根據個人偏好確定各自權重后提交上級，由上級綜合、確定參考權重，反饋給各下級單元并由其再次確定各自權重，再提交上級綜合，如此不斷反饋直至滿足一定終止條件，由上級最終確定系統綜合權重；Li Dengfeng等[20]以群體評價差異最小化為目標函數建立求解屬性權重的規劃模型；基于區間直覺模糊值熵最大化思想，戚筱雯等[21]提出一種確定屬性權重的決策方法；郭凱紅和李文立[22]提出一種在缺失權重信息前提下，基于證據距離和模糊熵權變換的多屬性群決策放閥，利用決策矩陣客觀確定決策者權重及屬性權重；Zhang Zhen和Guo Chonghui[23]以個體評價值與群體評價均值偏差最小化為準則建立規劃模型求解權重。上述客觀賦權結果雖然在很大程度上避免了主觀因素影響，但有時會出現與實際重要程度相偏離的情況。針對主、客觀賦權法各自的局限性，基于不同研究視角的主客觀綜合賦權法應運而生：Ma Jian等[24]將決策者提供的主觀信息與現實客觀信息相結合，建立雙目標決策模型來決定屬性權重；Rao和Patel[25]依據數據的方差比例確定客觀權重，并按照不同比例與主觀權重進行集成；閆書麗等[18]依據備選方案與理想方案間的灰色關聯度和極大熵原理建立求解客觀權重的規劃模型，并與決策者提供的主觀權重進行集成獲得屬性的綜合權重。

本文著眼于屬性指標權重的確定，將群體看作由多個獨立成員組成，每個成員在共同的多重屬性下被評價、并均參與到屬性權重的決策過程中。提出一種交互式迭代算法，從重要性無差異的均等權重出發，在設定的權重參數下分別對每一成員求解其決定最優權重的含參規劃模型，將所有成員針對各屬性所提供的優化權重進行算術平均，并將此平均結果作為新的權重參數代入規劃模型中以替換前一次迭代中的對應參數值。上述過程如此往復，直至任一成員在相鄰兩次迭代的參數權重下加權綜合屬性值的絕對差異控制在非阿基米德無窮小量以內，則迭代過程終止，此時使用的參數權重即為各屬性的最優權重，相應可以計算各群成員的最優加權綜合屬性值，作為排序選擇的依據。由于迭代計算過程由所有群體成員共同參與和決定，故可以認為最終優化和選擇結果為絕大部分成員所接受并滿意。相比較于前人已有的關于屬性指標權重的研究成果，本文所提出的交互式群決策評價方法展現出易于求解、可操作性強、適用范圍更廣、便于推廣應用等優勢。

2 多屬性群決策下的交互式評價

假定屬性i的參數權重為wi,i=1,…,m，對于成員k而言，可以在如下前提約束下選取優化權重以最大化自身的加權綜合分值：在優化權重下成員k與其他各成員在加權綜合屬性值的最大絕對差距不能高于在參數權重下的這一最大絕對差距。也就是說，成員k不被允許選取擴大其與其他成員距離的權重。令wik,i=1,…,m為成員k所建議的優化權重變量，針對上述思想進行建模，提出如下模型(1)：

wik≥0,i=1,…,m

(1)

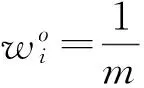
(2)

(3)

由于新變量fk(wik)≥0，故不等式組(3)可以等價轉化為如下不等式組(4)：

fk(wik)≥0

(4)

表1 算例分析

fk(wik)≥0,wik≥0,i=1,…,m

(5)

3 算例分析與實際應用

3.1 算例分析

為了展示上述交互式迭代方法的具體過程，考慮如下由五個成員所組成的算例群體G，每個成員均在統一的四種屬性指標下按照1到10的分值進行表現評價，具體得分見表1中第2至5列。

圖1直觀展示了各個成員對于最優加權綜合分值的尋優過程，其中橫軸代表迭代次數，縱軸代表加權得分。

圖1 加權分值的迭代尋優過程

3.2 研發項目選擇的應用

以下將上述交互式群決策評價方法應用于土耳其鋼鐵行業中研發項目申請的投資選擇決策。相關數據由37項研發項目申請組成，最早被Oral等[26]使用，之后依次被Green等[27]和Liang Liang等[28]所研究。每個項目包含兩大類共6項評價指標，一類是預算指標，即完成該項目的預期預算，另一類是貢獻指標，包括直接經濟貢獻、間接經濟貢獻、技術貢獻、科學貢獻和社會貢獻。具體數據見表2第1至7列所示。由于預期預算是一種成本型屬性，數值越小表示業績越優，因此在評價中屬于越小越好的負向指標。為了便于與其它5項正向貢獻指標或效益型屬性相結合進行綜合評價，對所有預算數據進行統一調整處理轉化為其相反數(見表2最后一列)，調整后預算即成為越大越好的正向指標。

另一方面，不同指標下數據由于計量單位的差異，存在綜合評價時的可比性問題。為了消除不同屬性量綱的影響，采用數據標準化方法進行處理。具體采用MIN-MAX標準化或離差標準化對數據進行線性變換：對于每一貢獻指標和調整后預算指標下的數據，與該指標下所有數據極小值作差的結果，除以該指標下所有數據的極差(即極大值與極小值之差)。經過上述標準化處理后的數據均落在區間[0，1]之內，具體結果列于表3中。

本文的交互式迭代方法與基于交叉效率的其它方法在模型選擇和機制設計上存在明顯差異，具體來說：本文從多屬性群決策的研究視角出發，將備選項目看作接受評價且參與權重確定的群成員，所有評價指標(包括預算指標和貢獻指標)構成多屬性指標，經過交互式迭代過程的計算，得到最優屬性權重以及各成員相應的最優加權綜合屬性值，作為排序選擇的依據；而基于交叉效率的其它方法，則是以數據包絡分析交叉效率模型為基礎，將所有評價指標區分為投入(即預算指標)與產出(即貢獻指標)兩大類代入模型求解。然而在最終的排序和選擇結果上卻基本可以達成一致，說明本文提出的交互式群決策評價方法是合理且有效的。

表2 研發項目數據

表3 標準化研發數據

各種方法下所有入選研發項目的預期預算總和顯示于表4最后一行，其中本方法資助額度為957.4，Liang Liang等[28]和Green等[27]給出的資助額度分別為994.7和982.9。雖然基于本文提出的交互式群決策評價方法下的項目選擇結果相比較于前人工作，在充分利用總預算上限上稍顯遜色，但是該方法也具有以下明顯優勢。

首先，本文方法需要反復求解的模型(5)不僅是線性規劃，而且規模很小、約束條件簡單，迭代求解過程簡便易操作，具有很強的實用普及性。其次，基于交叉效率的評價方法需要在所有指標中區分出投入和產出指標，否則無法利用數據包絡分析模型進行求解，這一點極大約束了該類方法的運用范圍，無法處理投入或產出指標缺失的決策案例；而在本文方法下，所有指標構成多屬性評價指標，不必區別投入和產出，因此本文方法實際應用范圍更為廣泛，可以解決交叉效率方法無法處理的特殊決策情形。

表4 研發項目選擇結果

4 結語

群體決策方式在解決復雜現實決策問題中的優勢日益彰顯并在各個領域得到廣泛運用，多屬性群決策問題已成為現代決策科學的重要組成部分。本文針對多屬性群決策中屬性指標權重的確定，提出一種交互式迭代算法，以均等屬性權重為起點進入迭代過程，在給定的權重參數下分別對每一成員求解含參規劃模型并得到與其相關的一組優化權重。將所有成員針對各屬性所提供的優化權重結果進行算術平均，并作為新的權重參數代入規劃模型中以進入下一輪迭代計算。重復上述過程直至任一群成員在相鄰兩次迭代的參數權重下加權綜合屬性值的絕對差異控制在非阿基米德無窮小量以內，則迭代過程終止，此時使用的參數權重即為各屬性的最優權重。實際迭代計算過程由所有群體成員共同參與和決定，故可以認為最終優化和選擇結果為絕大部分成員所接受并滿意。

上述交互式多屬性群決策評價方法所依賴的主要數學模型可以等價轉化為線性規劃模型，具有易于求解、可操作性強、適用范圍廣泛、便于推廣應用等優勢。后續研究可以進一步考慮如何將本文中的交互式迭代思想運用至多屬性群決策中決策專家的權重確定。

[1] Bryson N. Group decision-making and the analytic hierarchy process: Exploring the consensus-relevant information content [J]. Computers & Operations Research, 1996, 23(1): 27-35.

[2] Herrera-Viedma E, Herrera F, Chiclana F. A consensus model for multiperson decision making with different preference structures [J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2002, 32(3): 394-402.

[3] 徐澤水. 純語言多屬性群決策方法研究 [J]. 控制與決策，2004，19(7)：778-781.

[4] 王學軍，郭亞軍. 基于G-1法的群決策集結分析 [J]. 中國管理科學，2004,12(S1)：14-16.

[5] 徐迎軍，李東. 多屬性群決策達成一致方法研究 [J]. 控制與決策，2010，25(12)：1810-1820.

[6] 尤天慧，李洪燕，劉彩娜. 一種具有不確定偏好序信息的多指標群決策方法 [J]. 中國管理科學，2013，21(5)：110-114.

[7] Ramanathan R, Ganesh L S. Group preference aggregation methods employed in AHP: An evaluation and an intrinsic process for deriving members’ weightages [J]. European Journal of Operational Research, 1994, 79(2): 249-265.

[8] 孟波，付微. 一種有限方案多目標群決策方法 [J]. 系統工程，1998，16(4)：57-61.

[9] 宋光興，鄒平. 多屬性群決策中決策者權重的確定方法 [J]. 系統工程，2001，19(4)：84-89.

[10] 梁樑，王國華. 一種群決策中專家客觀權重的確定方法 [J]. 系統工程與電子技術，2005，4：652-655.

[11] Yue Zhongliang. A method for group decision-making based on determining weights of decision makers using TOPSIS[J]. Applied Mathematical Modelling, 2011, 35(4): 1926-1936.

[12] Yue Zhongliang. Extension of TOPSIS to determine weight of decision maker for group decision making problems with uncertain information [J]. Expert Systems with Applications, 2012, 39(7): 6343-6350.

[13] 梁昌勇，戚筱雯，丁勇，等. 一種基于TOPSIS的混合型多屬性群決策方法 [J]. 中國管理科學，2012，20(4)：109-117.

[14] 蔣文能. 群組決策中專家權重確定的思路和方法 [J]. 統計與決策，2013，2：24-28.

[15] Chen C, Chau K W. Three-person multi-objective integrated approach to determine attribute weights [J]. European Journal of Operational Research, 2002, 142(3): 625-631.

[16] Chen Zhiping, Yang Wei. A new multiple attribute group decision making method in intuitionistic fuzzy setting[J]. Applied Mathematical Modelling, 2011, 35: 4424-4437.

[17] Xu Z S, Yager R R. Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group [J]. Fuzzy Optimization and Decision Making, 2009, 8(2): 123-139.

[18] 閆書麗，劉思峰，方志耕，等. 區間灰數群決策中決策者和屬性權重確定方法 [J]. 系統工程理論與實踐，2014，34(9)：2372-2378.

[19] 梁樑，王國華. 多層次交互式確定權重的方法 [J]. 系統工程學報，2002，17(4)：358-363.

[20] Li Dengfeng, Chen Guohong, Huang Zhigang. Linear programming method for multiattribute group decision making using IF sets [J]. Information Sciences, 2010, 180(9): 1591-1609.

[21] 戚筱雯，梁昌勇，張恩橋，等. 基于熵最大化的區間直覺模糊多屬性群決策方法 [J]. 系統工程理論與實踐，2011，31(10)：1940-1948.

[22] 郭凱紅，李文立. 權重信息未知情況下的所屬性群決策方法及其拓展 [J]. 中國管理科學，2011，19(5)：94-103.

[23] Zhang Zhen, Guo Chonghui. A method for multi-granularity uncertain linguistic group decision making with incomplete weight information [J]. Knowledge-Based Systems, 2012, 26(2): 111-119.

[24] Ma Jian, Fan Zhipeng, Huang Lihua. A subjective and objective integrated approach to determine attribute weights [J]. European Journal of Operational Research, 1999, 112(2): 397-404.

[25] Rao R V, Patel B K. A subjective and objective integrated multiple attribute decision making method for material selection [J]. Materials & Design, 2010, 31(10): 4738-4747.

[26] Oral M, Kettani O, Liang P. A methodology for collective evaluation and selection of industrial R&D projects [J]. Management Science, 1991, 37(7): 871-883.

[27] Green R, Doyle J, Cook W D. Preference voting and project ranking using DEA and cross-evaluation [J]. European Journal of Operational Research, 1996, 90(3): 461-472.

[28] Liang Liang, Wu Jie, Cook W D, et al. The DEA game cross efficiency model and its Nash equilibrium [J]. Operations Research, 2008, 56(5): 1278-1288.

A Study on the Interactive Evaluation in Multiple Attribute Group Decision Making

DU Juan, HUO Jia-zhen

(School of Economics and Management, Tongji University, Shanghai 200092,China)

In this paper, a group is composed of dependent members who are supposed to be evaluated via multiple attributes and participation in determining these attributes’ weights. In order to seek the attributes’ weights in multiple attribute group decision making, an iterative algorithm is proposed, which starts with equal weights and solves a programming model with weight parameters for each group member to obtain a set of optimal weights. The optimal weights to each attribute decided by every group member are then averaged and used as the new weight parameters in modeling solving during the next iteration. This iterative procedure repeats until for each member, the consecutive weighted average values of all attributes converge within a specified small enough positive value. The optimal attributes’ weights of the group are therefore obtained as the current parameter weights when the iteration terminates. Such a set of attributes’ weights are jointly determined by all group members, in which sense the related results and decisions are supposed to be accepted and satisfied by all (or at least most) members. A numerical example and an application of R&D project selection are studied to demonstrate the feasibility and effectiveness of the proposed method.

group decision making; attributes’ weights; interactive iteration

1003-207(2016)11-0120-09

10.16381/j.cnki.issn1003-207x.2016.11.014

2016-01-10；

2016-04-30

國家自然科學基金面上項目(71471133)

杜娟(1984-)，女(漢族)，安徽合肥人，同濟大學經濟與管理學院，副教授，研究方向：數據包絡分析、決策與優化、多目標決策系統，E-mail：dujuan@tongji.edu.cn.

C934

A