需求不確定下承諾交貨時間和產能決策

謝祥添，張畢西

(1.廣東開放大學/廣東理工職業學院，廣東 廣州 510091；2.廣東工業大學管理學院，廣東 廣州 510520)

需求不確定下承諾交貨時間和產能決策

謝祥添1，張畢西2

(1.廣東開放大學/廣東理工職業學院，廣東 廣州 510091；2.廣東工業大學管理學院，廣東 廣州 510520)

在網上定制的市場中，需求具有數量和時間兩方面的不確定性。本文提出同時考慮需求量具有承諾交貨時間敏感性和隨機性，采用作業成本法建立以期望利潤為目標函數，以承諾交貨時間和產能為決策變量的模型。通過模型的分析得到了相互遞推的最優承諾交貨時間和最優產能數學表達式。在此基礎上，運用排隊理論建立了以承諾交貨時間可靠性為限制條件的M/M/1決策模型。通過模型分析，證明了模型是凹規劃，給出了最優承諾交貨時間和最優產能滿足的方程組。最后，通過算例的分析可知最優承諾交貨時間和最優產能受承諾交貨時間可靠性限制，而且隨著承諾交貨時間可靠性的提高，最優承諾交貨時間是遞增的，最優產能和最優期望利潤是遞減的。研究表明：結合承諾交貨時間可靠性確定最優承諾交貨時間和最優產能有助于提高產能的利用率和交貨時間的準確性。

不確定需求；產能；承諾交貨時間；M/M/1

1 引言

當前，客戶對交貨時間要求越來越高，時間已經僅次于價格成為企業贏得市場競爭優勢的因素[1]。較早提出時間成為企業競爭武器的是Stalk[2]，他提出時間因素正在重塑全球市場。隨后，Bozdogan等[3]通過分析日本企業的運營，提出日本企業能在全球市場競爭中占有一席之地的主要原因是重視時間的管理(基于時間的生產，基于時間的分銷和基于時間的創新)。Suri[4]提出了在時間競爭環境下快速反應制造(Quick Response Manufacturing,QRM)的優勢和策略。Rondeau等[5]通過對265家基于時間生產的企業調查分析，得出了基于時間生產能提高企業的標準化水平和整合能力。Nahm等[6]通過對224家基于時間生產的企業調查分析，得出了基于時間生產能顯著提高企業的決策和溝通能力。此外還有Fisher[7]，楊文勝等[8]，馬士華等[9]和Yang Daojian等[10]從供應鏈的角度研究如何運用時間來獲得競爭的優勢。So等[11]把企業運用時間獲得競爭優勢歸納為三種策略：1、快速服務；2、提前預約；3、承諾交貨時間。我國大部分生產企業，如訂單生產式(Make-to-order, MTO)企業，一般采用第三種策略。那么企業采用第三種策略，在不確定需求條件下，如何保證在承諾交貨時間內完工，承諾交貨時間應該多長和承諾交貨時間可靠性(部分文獻稱之為時間服務水平)就成為企業要解決的問題了，而解決這些問題無不與產能的配置有關。

關于承諾交貨時間和產能決策問題，最近十幾年受到眾多學者關注和研究。如，Lederer等[12]考慮需求是承諾交貨時間和價格敏感的，研究了價格、產能和承諾交貨時間三者聯合決策的問題，證明了它們存在著均衡關系，指出承諾交貨時間更短，產能柔性更大和生產成本更低的企業占有的市場份額更大，產能利用率更高和獲得的利潤更多。So等[11]根據承諾交貨時間可靠性較高時M/M/1排隊模型近似G/G/1排隊模型，運用排隊理論建立以企業利潤為目標函數，以價格，產能擴張和承諾交貨時間為決策變量的M/M/1模型研究了兩類(資本密集型和勞動密集型)服務企業的價格，承諾交貨時間和產能之間的關系，得到了這兩類企業的三個決策變量聯合最優解。Boyaci等[13]分析產能成本對兩類產品(常規產品和快速產品)的承諾交貨時間，承諾交貨時間可靠性和價格影響，建立這兩類產品的產能，承諾交貨時間，承諾交貨時間可靠性和價格決策模型，通過模型的分析得出了：當市場是需求價格敏感性時，企業可以采取價格差異化獲利；當市場是需求承諾交貨時間敏感性時，企業可以采取交貨時間差異化獲利；當市場是需求價格敏感性與承諾交貨時間敏感性相近時，企業可以提供交貨時間可靠性更低的快速產品獲得競爭優勢。最近，Park[14]考慮需求函數是價格，承諾交貨時間和時間服務水平函數，建立以供應商與零售商二級供應鏈利潤為目標函數，以產能，承諾交貨時間，時間服務水平和價格為決策變量模型，通過模型的求解得到了模型最優的產能，交貨時間，時間服務水平和價格。Falu等[15]和Knollmann等[16]針對延期交貨的問題，提出運用控制理論調整產能的增減和訂單的釋放來提高交貨時間的準確性。謝祥添等[17]考慮市場是需求承諾時間敏感性，研究了兩類(人工作業和自動化)訂單生產式企業承諾交貨時間和產能聯合決策問題，得出了最優的產能擴張與承諾交貨時間存在著類似于耐克函數的關系；最優的產能擴張與承諾交貨時間受承諾交貨時間可靠性限制。Jayaswal等[18]研究了需求是承諾時間和價格敏感性的雙寡頭競爭問題，得出了具有產能成本優勢的企業應該針對細分市場采用差異化的承諾交貨時間和價格策略。這與Boyaci和Ray[13]的結論類似。

以上文獻考慮需求是時間的不確定性，采用傳統的成本會計構建企業利潤目標函數得出最優決策變量使企業的利潤最大化。但是在現今復雜需求環境下，需求在數量上往往也具有不確定性。為適應這種需求的不確定，眾多企業采取柔性生產的方式。在產能上表現為：在需求高峰時，企業通過加班、雇傭臨時工和外包等方式增加產能；在需求低谷時，企業通過減少工人、工時等方式減少產能[19]。傳統成本會計不能準確核算這種產能變化的成本，導致產品成本的扭曲和產能的過剩與不足[20-21]。鑒于此，部分學者如Banker等[22]，Balakrishnan等[23]，G?x[24]和G?x[25]面對不確定需求采用了作業成本法核算產品和產能的成本，取得了一定的成果。因此，本文采用作業成本法核算產能成本，構建企業的期望利潤函數。

本文的貢獻在于考慮需求具有承諾交貨時間敏感性和數量上的不確定，采用作業成本法建立以期望利潤為目標函數，以承諾交貨時間和產能為決策變量的模型，得到了相互遞推的最優承諾交貨時間和產能數學表達式。在此基礎上，考慮需求時間間隔和產品生產處理時間服從負指數分布，建立M/M/1模型得到了最優承諾交貨時間和最優產能，這些研究有助于提高產能的利用率和交貨時間的準確性。

2 一般模型

2.1 模型的建立

考慮需求數量上的不確定和客戶傾向于較短的承諾交貨時間，建立需求函數為：

D(l)=a-bl+ε

(1)

其中，a為b=0和ε=0時的需求量，b為需求承諾交貨時間敏感系數(b≥0)，l為承諾交貨時間。交貨時間敏感性需求函數有線性的，如馬士華等[9]提出的供應鏈響應時間和價格敏感需求函數和Ho等[26]提出的承諾交貨時間和服務質量敏感需求函數；也有非線性的，如So等[11]提出的價格和承諾交貨時間敏感柯布-道格拉斯需求函數。為了便于研究產能與承諾交貨時間的關系，本文考慮承諾交貨時間敏感性需求函數是線性的。ε為隨機需求量，設其均值為E(ε)，這時需求量期望值為：E[D(l)]=a-bl+E(ε)。

根據作業成本法基本原理：產品消耗作業，作業消耗資源。則資源消耗量與產品之間的關系為：

zj=uj(a-bl+ε)=uj(a-bl)+Δj

(2)

其中，zj為第j種資源消耗量。uj為產品消耗作業j的單位作業量。Δj為產品隨機需求消耗第j種資源的數量，Δj=ujε，設其概率密度函數和概率分布函數分別為φ(Δj)和Φ(Δj)，設H(zj)為不含Δj的第j種資源的消耗量，H(zj)=uj(a-bl)。

建立以期望利潤為目標函數，以承諾交貨時間和產能為決策變量的數學模型為:

(3)

(3)式由三項構成，第一項表示期望收入；第二項表示產能成本；第三項表示產能不足的懲罰成本(銷售機會損失)，其中第j種資源不足是指產品的消耗量大于當前產能：zj>xj，這時有H(zj)+Δj>xj，移項Δj>xj-H(zj)。那么，用積分表示為：

(3)式其余參數p為單價，c為單位生產成本(除產能成本)。X為產能向量，X=x1，x2，x3…xm，xj為第j種資源的產能。vj為第j種資源的產能單位成本。ωj為第j種資源的產能沒有滿足需求時的懲罰系數，由于需求不確定，第j種資源的產能有可能不能滿足需求，由此導致企業的銷售機會損失。一般情況，這種損失產生的成本比正常產能成本要高，例如，需求增加，現有產能不能滿足需求時，企業通過加班的方式增加產能，企業付出的加班費比正常工資高。因此有，ωj>1。

2.2 模型的分析

(1)考慮只有承諾交貨時間為決策變量

對(3)式求承諾交貨時間l一階偏導數等于0有：

(4)

從(4)式可知，最優承諾交貨時間滿足的等式為：滿足需求得到的單位利潤(p-c)等于沒有滿足需求失去的單位銷售機會損失。對(4)式化簡有：

(5)

其中，Φ-1(x)為Φ(x)的反函數，設l*是等式(5)關于l的解。對(3)式求承諾交貨時間l的二階偏導數有：

(6)

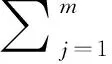
(2)考慮只有產能為決策變量

同理，對(3)式求產能xj的一階偏導數等于0有：

(7)

對(3)式求產能xj的二階偏導數有：

(8)

從(7)式和(8)式知，若φ[xj-H(zj)]>0，那么目標函數存在最大值，最優產能是等式(7)關于產能xj的解，設為xj*。

(3)同時考慮承諾交貨時間和產能為決策變量

一般而言，企業對產品進行承諾交貨時間和產能決策時，已經存在著市場的交貨時間，設為l(0)。在l(0)前提下，企業可以根據(7)式和(8)式確定產品的最優產能，設為xj(0)*，這時企業得到第一次決策的最優期望利潤。接著，企業可以在xj(0)*前提下，根據(5)式和(6)式得到產品的最優承諾交貨時間，設為l(0)*，這時企業得到了第二次決策的最優期望利潤。如此反復，可得到最優承諾交貨時間和最優產能。

當然了，企業也可以根據自身已有的產能作為初始產能，然后在初始產能條件下決定最優的承諾交貨時間。余下的決策過程與上述一致，略。

以上只是從企業獲得期望利潤最大化角度，對承諾交貨時間和產能決策。但是，交貨時間的長短受生產過程的限制[27]。接下來，我們研究生產過程近似M/M/1排隊模型的承諾交貨時間和產能決策問題。

3 M/M/1 模型

3.1 模型的假設

(1)生產過程近似M/M/1排隊模型，即單一產品，單一服務臺(資源)，產品到達時間間隔服從負指數分布，產品生產處理時間服從負指數分布，以及產品先來先服務的生產過程；

(2)產能為單位時間處理產品數，設為x；需求量為單位時間的需求。

3.2 模型的建立

Abate等[28]指出承諾交貨時間可靠性較高時，實際交貨時間小于等于承諾交貨時間的尾概率(Tail-probabilities)分布近似服從以下指數分布：

1-P{L(l,x)≤l}≈γe-ηl

(9)

其中，L(l,x)為實際交貨時間，它是關于承諾交貨時間和產能函數。P{L(l,x)≤l}為實際交貨時間小于等于承諾交貨時間的概率。γ為常項，η為衰減率。為了敘述方便下文統一用=替換≈。

對于M/M/1排隊模型，P{L(l,x)≤l}尾概率分布服從γ=1，η=x-E[D(l)]的指數分布[11,26]，即： 1-P{L(l,x)≤l}=e-{x-E[D(l)]}l。那么，承諾交貨時間可靠性限制條件表達式為：

P{L(l,x)≤l}=1-e-{x-E[D(l)]}l≥α

(10)

其中，α為承諾交貨時間可靠性，α∈(0, 1)。

那么，考慮承諾交貨時間可靠性，建立以單位時間期望利潤為目標函數，以承諾交貨時間和產能為決策變量的M/M/1模型為：

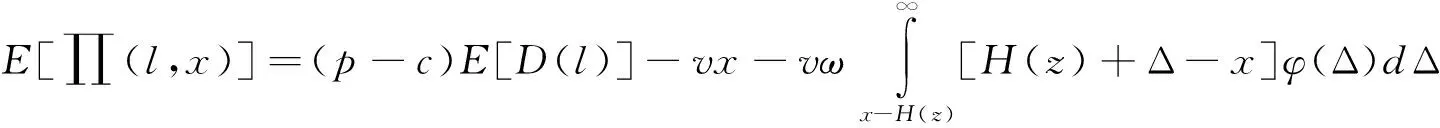
s.t.P{L(l,x)≤l}=1-e-{x-E[D(l)]}l≥α

(11)

3.3 模型的分析

命題1 (11)式為凹規劃。

證明：因為(11)式的目標函數海賽矩陣：

為半負定的，所以(11)式的目標函數為凹函數。又因為(11)式中限制條件表達式e-{x-E[D(l)]}l，設之為g(l,x)，為凸函數，證明見附錄1。根據凹規劃的定義，(11)式為凹規劃。

命題1結論：根據(11)式為凹規劃性質可知，最優解滿足(11)式的拉格朗日函數一階偏導數為0的條件。即最優解是以下方程組的解:

(12)

其中，λ為拉格朗日乘子；?=1-α。

4 算例

某一家用電器生產企業，部分產品采用網上定制的方式銷售，其過程為：客戶通過企業網站定制產品，企業根據客戶要求生產，生產完畢后交付。其中有一產品A，采用網上定制銷售后，出現了產能不平衡和延期交貨頻繁的問題，因此需要為其確定合適的產能和承諾交貨時間。

產品A，根據歷史數據統計可知：客戶下單購買的時間間隔服從負指數分布，均值為500- 50l+E(ε)個/天，其中需求隨機變量ε～U(5,10)。產品A的生產時間服從負指數分布，平均每個產品的生產處理時間為1/x天。又已知每個產品A價格為2萬元，生產成本為1萬元，產能成本為0.2萬元，消耗單位作業量為0.5以及缺貨懲罰系數為1.1。(一)若忽略企業的生產過程，市場的交貨時間為10天，求產品A的最優承諾交貨時間和最優產能。(二)根據企業的生產過程，分析產品A承諾交貨時間可靠性的敏感性，以及當它的承諾交貨時間可靠性要求在90%以上時，最優承諾交貨時間和最優產能為多少？

依題意，產品A需求隨機變量ε～U(5,10)，所以其消耗的生產資源△～U(2.5,5)。其余參數p=2萬元，c=1萬元，v=0.2萬元，a=500個，u=0.5，b=50，w=1.1。

(一)忽略企業的生產過程

把相關數據代入(8)式得-0.088<0，所以根據(7)式得最優產能x*=252.7272727-25l，把l(0)=10天=l代入得x(0)*=2.7272727個/天，這時最優期望利潤為6.7273萬元。又由(6)式得-55<0，所以根據(5)式得最優承諾交貨時間l*=9.290909091-0.04x，把x(0)*=2.7272727個/天=x代入得l(0)*=9.181818183天，這時最優期望利潤為25.1364萬元。

余下的最優承諾交貨時間和產能可以通過遞推公式求得，遞推公式為：

(13)

其中，n=1,2,3…N。

通過(13)式和上文已計算的x(0)*與l(0)*可得最優的承諾交貨時間和產能決策過程，如表1所示。

表1 最優承諾交貨時間和產能決策

注：根據承諾交貨時間和產能的變化趨勢，最優的決策為承諾交貨時間等于0(若決策得到的是負數，根據承諾交貨時間大于0，則把負數設為0)。

(二)不忽略企業的生產過程

由算例可知企業的生產過程為M/M/1排隊模型，所以把相關數據代入(11)式化簡有：

E[∏(l,x)]=-2353.6-511l+22.24x-2.2lx-27.5l2-0.044x2

(14)

(1)產品A承諾交貨時間可靠性的敏感性分析

由命題1的結論可得最優解(l*,x*,λ*)與承諾交貨時間可靠性α(?=1-α)的關系。其中l*滿足以下一元四次方程：

22×(5l)4-1031×(5l)3-[1121×ln(1-α)]×5l-22×ln(1-α)2=0

(15)

x*為：

x*=0.227×[1112×ln(1-α)-220×ln(1-α)×l*-2750×(l*)3+25775×(l*)2]/ln(1-α)

(16)

(a)承諾交貨時間可靠性與最優承諾交貨時間和產能分析

對(15)式作圖可得l*和α關系，如圖1所示。從圖1可知，隨著承諾交貨時間可靠性的提高，最優承諾交貨時間是遞增的，并且遞增得越來越快。

對(16)式作圖可得x*和α關系，如圖2所示。從圖2可知，隨著承諾交貨時間可靠性的提高，最優產能是下降的，并且下降得越來越快。需指出的，隨著承諾交貨時間可靠性的提高，最優產能下降的原因是承諾交貨時間可靠性提高，承諾交貨時間增加，根據需求是交貨時間線性減函數。那么，需求減少。又根據作業成本法，需求減少，則對應的資源減少，所需的產能也就下降了。

(b)承諾交貨時間可靠性與最優期望利潤分析

把l*和x*代入(14)式得最優期望利潤函數E[Π(l*,x*)]與α關系，如圖3所示。隨著承諾交貨時間可靠性的提高，企業的最優期望利潤是下降的，并且下降得越來越快。

(2)產品的交貨時間可靠性在90%以上

依題意，有α=90%，把它代入(15)式和(16)式可得l*= 9.383天和x*= 38.575個/天，最優期望利潤為16.1404萬元/天。

為了弄清承諾交貨時間，產能和期望利潤之間的關系。現設y=0.1-e-(x-1015/2+50l)l，作y，E[Π(l,x)]和l，x的關系，如圖4所示。從圖4和(14)式可知，最優解是在曲面y與平面0相交線投影在E[Π(l,x)]表面上，再在其軌跡上找到的某一點使得E[Π(l,x)]值最大。

圖1 圖l*和α關系

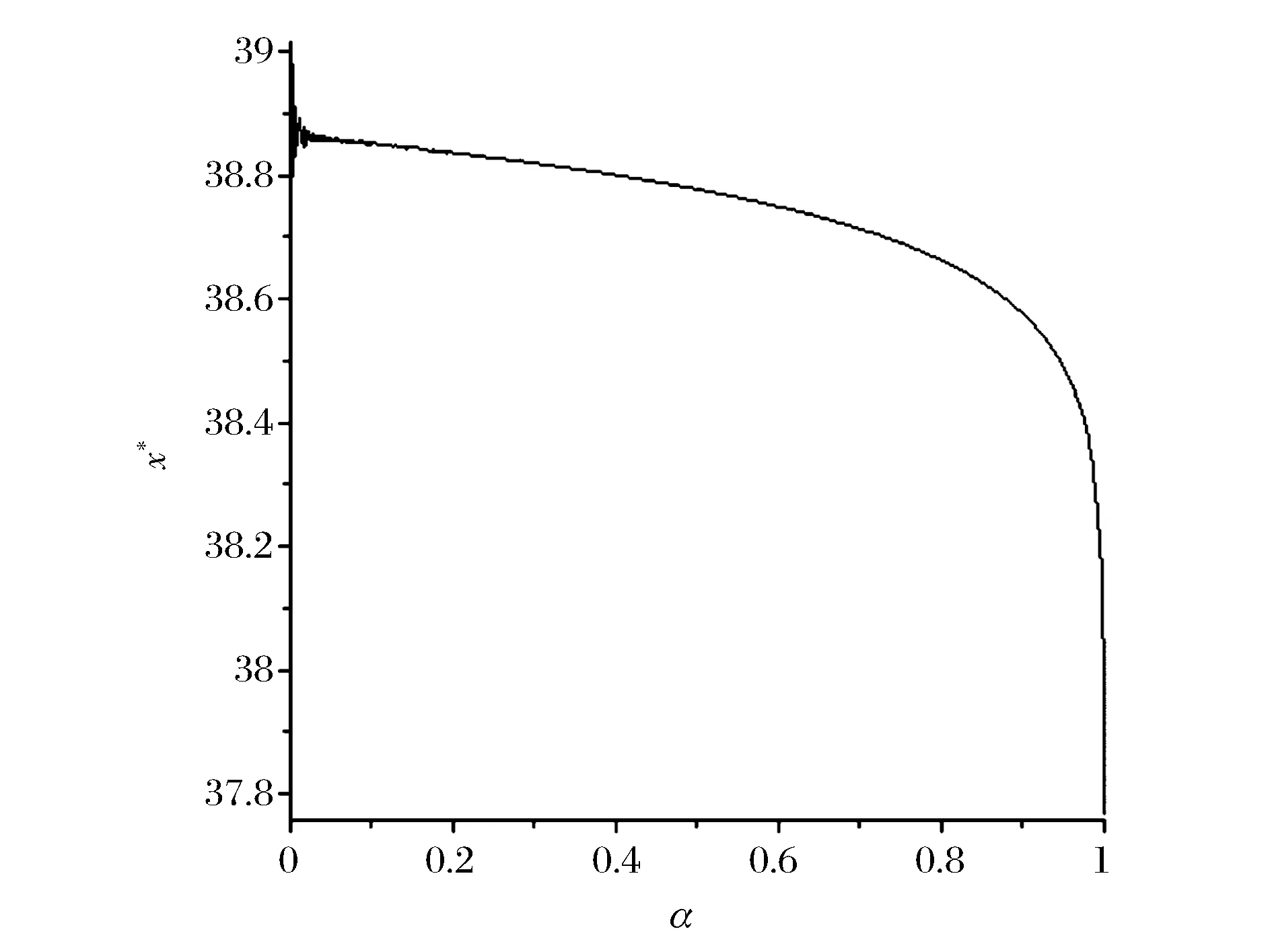
圖2 x*和α關系

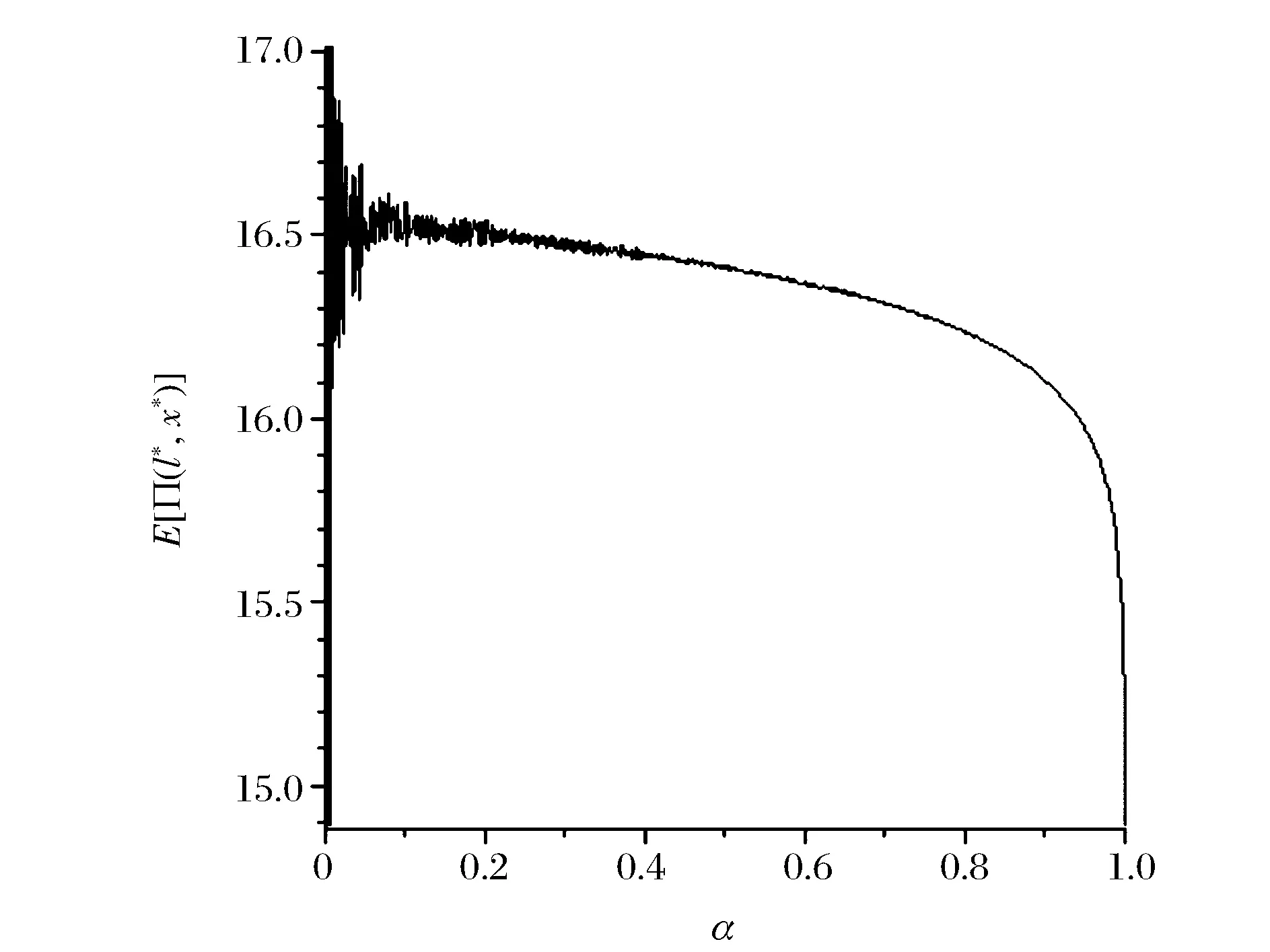
圖3 E[Π(l*,x*)]與α關系

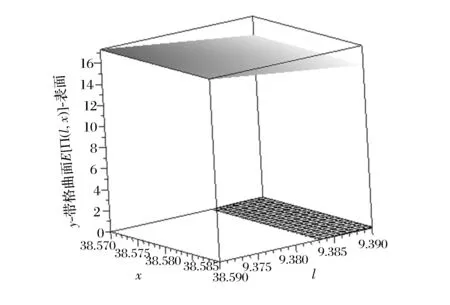
圖4 y，E[Π(l, x)]和l，x的關系

5 結語

從算例可知，當不考慮企業的生產過程時，企業最優期望利潤隨著決策的次數增加而增加，最終會增加至承諾交貨時間為0，企業取得最大的期望利潤。但是承諾交貨時間為0明顯與企業的實際相違背。所以我們考慮承諾交貨時間的可靠性，結合企業生產過程，得到了符合企業自身承諾交貨時間可靠性(承諾交貨時間可靠性在90%以上)的最優承諾交貨時間和產能。同時，通過算例對承諾交貨時間可靠性的敏感性分析可知：隨著承諾交貨時間可靠性的提高，最優承諾交貨時間是遞增的，最優產能和最優期望利潤是遞減的。

當今企業面對不確定的市場需求不僅是需求時間的不確定，還會是需求數量的不確定。針對傳統成本會計在需求量不確定條件下不能準確核算產能成本，本文采用作業成本法建立了承諾交貨時間和產能為決策變量的期望利潤模型。在此基礎上，考慮需求時間的不確定和承諾交貨時間可靠性，根據企業生產過程，運用排隊理論建立了承諾交貨時間和產能為決策變量的M/M/1模型。通過對模型的分析證明了M/M/1模型為凹規劃，給出了最優承諾交貨時間和最優產能滿足的方程組。

本文的M/M/1模型是在假設企業生產過程為M/M/1的前提下建立的。在實際當中，企業生產過程一般為G/G/1。根據排隊理論可知，當承諾交貨時間可靠性較高時(一般為95%以上)[11]，M/ M/1排隊模型近似于G/G/1排隊模型。因此，本文的M/M/1模型可推廣應用于承諾交貨時間可靠性較高生產過程為G/G/1的企業。

本文研究的是自由競爭市場中的訂單生產式企業，價格受市場影響。所以把價格看作常量。但是在市場經濟中會存在著價格壟斷的企業，它們具有價格的決定權。因此，在不確定需求下，建立以企業期望利潤為目標函數，以價格、承諾交貨時間和產能為決策變量的模型將會是我們要研究的。

附錄1：g(l,x)=e-{x-E[D(l)]}l為凸函數

引理1f(x,y)是二元函數，當f(x,y)?R2時，f(x,y)是凸函數的充要條件是[29]：

引理2 如果f和g是凸函數，且g遞增，那么h(x)=f(g(x))是凸函數。

證明：設g(l,x)=e-G(x,l),G(x,l)={x-E[D(l)]}l。

因為E[D(l)]=a-bl+E(ε)，所以有：G(x,l)={x- [a-bl+E(ε)]}l。根據引理1得：

所以，G(x,l)為凸函數。又因為設x10，又因為l>0，所以x-E[D(l)]>0。那么，x2-[a-bl2+E(ε)]>0，則有：G(x2,l2)>G(x2,l1)。又因為G(x2,l1)-G(x1,l1)= {x2-[a-bl1+E(ε)]-{x1-[a-bl1+E(ε)]}}l1= (x2-x1)l1>0，所以G(x2,l1)>G(x1,l1)。所以，G(x,l)為增函數。又因為e為底的負指數函數是凸函數，所以根據引理2可知g(l,x)為凸函數，至此證畢。□

[1]BallouRH.Businesslogisticsmanagement[M].UpperSaddleRiver:PrenticeHall,1998.

[2]StalkG.Competingagainsttime:Howtime-basedcompetitionisreshapingglobalmar[M].London:CollierMacmillan: 1990.

[3]BozdoganK,DeystJ,HoultD.Supplierintegrationintodesignanddevelopment[J].Robitics&AutomousSystems,2013,6(3):197-198.

[4]SuriR.Quickresponsemanufacturing:Acompanywideapproachtoreducingleadtimes[M].ProductivityPress, 1998.

[5]RondeauPJ,VonderembseMA,Ragu-NathanTS.Exploringworksystempracticesfortime-basedmanufacturers:Theirimpactoncompetitivecapabilities[J].JournalofOperationsManagement, 2000, 18(5): 509-529.

[6]NahmAY,VonderembseMA,KoufterosXA.Theimpactoforganizationalstructureontime-basedmanufacturingandplantperformance[J].JournalofOperationsManagement, 2003, 21(3): 281-306.

[7]FisherML.Whatistherightsupplychainforyourproduct?[J].HarvardBusinessReview, 1997, 75(2): 105-117.

[8] 楊文勝,李莉.響應時間不確定下的交貨期相關定價研究[J].中國管理科學,2005,13(2):56-62.

[9] 馬士華,王福壽.時間價格敏感型需求下的供應鏈決策模式研究[J].中國管理科學,2006,14(3):13-19.

[10]YangDaojian,QiErshi,LiYajiao.Quickresponseandsupplychainstructurewithstrategicconsumers[J].Omega, 2015, 52: 1-14.

[11]SoKC,SongJS.Price,deliverytimeguaranteesandcapacityselection[J].EuropeanJournalofOperationalResearch, 1998, 111(1): 28-49.

[12]LedererPJ,LiL.Pricing,production,scheduling,anddelivery-timecompetition[J].OperationsResearch, 1997, 45(3): 407-420.

[13]BoyaciT,RayS.Theimpactofcapacitycostsonproductdifferentiationindeliverytime,deliveryreliability,andprice[J].ProductionandOperationsManagement, 2006, 15(2): 179-197.

[14]ParkS,HongK.Optimalguaranteedservicetimeandserviceleveldecisionwithtimeandservicelevelsensitivedemand[J].MathematicalProblemsinEngineering, 2014,2014:1-7.

[15]FaluI,DuffieN.Adaptiveduedatedeviationregulationusingcapacityandorderreleasetimeadjustment[J].ProcediaCIRP, 2014, 17: 398-403.

[16]KnollmannM,WindtK,DuffieN.Evaluationofcapacitycontrolandplannedleadtimecontrolinacontrol-theoreticmodel[J].ProcediaCIRP, 2014, 17: 392-397.

[17] 謝祥添,張畢西.基于需求交貨時間敏感性交貨時間與產能決策[J].系統工程理論與實踐,2015,35(9):2242-2250.

[18]JayaswalS,JewkesEM.Priceandleadtimedifferentiation,capacitystrategyandmarketcompetition[J].InternationalJournalofProductionResearch, 2016, 54(9): 2791-2806.

[19] 張菊亮,張明玉.能力規劃、促銷與庫存控制集成決策[J].系統工程學報,2008,23(6):659-665.

[20]CooperR,KaplanRS.Howcostaccountingsystematicallydistortsproductcosts[M]//BrunsJr.WJ,kaplanRS.Accountingandmanagement:Fieldstudyperspectives,Boston:HarvardBusinessSchoolPress,1987: 204-228.

[21]KaplanRS.Researchopportunitiesinmanagementaccounting[J].JournalofManagementAccountingResearch, 1993, 5(3): 1-14.

[22]BankerRD,HughesJS.Productcostingandpricing[J].AccountingReview, 1994,69(3): 479-494.

[23]BalakrishnanR,SivaramakrishnanK.Sequentialsolutionstocapacity-planningandpricingdecisions[J].ContemporaryAccountingResearch, 2001, 18(1): 1-26.

[24]G?xRF.Theimpactofcost-basedpricingrulesoncapacityplanningunderuncertainty[J].SchmalenbachsBusinessReview, 2001, 53(3): 197-228.

[25]G?xRF.Capacityplanningandpricingunderuncertainty[J].JournalofManagementAccountingResearch, 2002, 14(1): 59-78.

[26]HoTH,ZhengYusheng.Settingcustomerexpectationinservicedelivery:Anintegratedmarketing-operationsperspective[J].ManagementScience, 2004, 50(4): 479-488.

[27]NoblesseAM,BouteRN,LambrechtMR,etal.Lotsizingandleadtimedecisionsinproduction/inventorysystems[J].InternationalJournalofProductionEconomics, 2014, 155: 351-360.

[28]AbateJ,ChoudhuryGL,WhittW.Exponentialapproximationsfortailprobabilitiesinqueues,I:Waitingtimes[J].OperationsResearch, 1995, 43(5): 885-901.

[29] 方逵,朱幸輝,劉華富.二元凸函數的判別條件[J].純粹數學與應用數學, 2008,24(1):97-101.

Promised Lead Time and Capacity Decision-Making Based on Demand is Uncertain

XIE Xiang-tian1，ZHANG Bi-xi2

(1.The open University of Guangdong/Guangdong Polytechnic Institute, Guangzhou 510091,China;2.School of Management,Guangdong University of Technology, Guangzhou 510520, China)

In the market of online-customized products, demands possess uncertainty in both amount and time.In this paper, a promised lead time and capacity decision-making model is proposed by taking expected profit as the objective function with the Activity Based Costing, considering the demands are sensitivity of promised lead time and stochastic. A recursive mathematical expression of the optimal promised lead time and the optimal capacity is obtained by analyzing the model. On this basis, building up the M/M/1 model by taking the reliability of promised lead time as limiting condition with the queuing theory. It is proved that the M/M/1 model is Concave Programming, and equations of the optimal promised lead time and the optimal capacity are obtained. At last, through numerical example the optimal promised lead time and the optimal capacity are restricted by the reliability of promised lead time, and with the improvement of the reliability of promised lead time, the optimal promised lead time is increasing; the optimal capacity and the optimal expected profit are decreasing. The research shows that the optimal promised lead time and the optimal capacity are got through combining with the reliability of the promised lead time, which can improve the utilization rate of capacity and the accuracy of lead time.

uncertain demand; capacity; promised lead time; M/M/1

1003-207(2016)11-0073-08

10.16381/j.cnki.issn1003-207x.2016.11.009

2015-03-13；

2015-08-04

國家自然科學基金資助項目(71271060，70971026)；廣東省自然科學基金資助項目(S2012010009278，2014A030310285)；廣東理工職業學院資助項目(1610)

謝祥添(1981-)，男(漢族)，廣東清遠人，廣東開放大學講師，博士生，研究方向：管理科學與工程，E-mail:122627748@qq.com.

C934

A